JQX/进取芯 席明纳第23期（2025.12.25）

洛伦兹力冲量的应用

一、洛伦兹力的冲量

带电粒子在匀强磁场中运动时，所受洛伦兹力方向与速度方向时刻垂直。洛伦兹力的冲量可以通过累加进行计算。
$$ \mathbf{I} = \int \mathbf{F} \, dt = \int q \, (\mathbf{v} \times \mathbf{B}) \, dt = q \left( \int \mathbf{v} \, dt \right) \times \mathbf{B} = q \, \mathbf{x} \times \mathbf{B} $$
其中，$\mathbf{x} = \int \mathbf{v}$, $dt$ 为粒子从初始时刻到末时刻的位移矢量。该冲量的方向由叉积决定，始终垂直于位移矢量 $\mathbf{x}$ 与磁场 $\mathbf{B}$ 所构成的平面，即同时垂直于 $\mathbf{x}$ 和 $\mathbf{B}$。其大小为 $|\mathbf{I}| = q B x \sin\theta$，$\theta$ 为 $\mathbf{x}$ 与 $\mathbf{B}$ 的夹角。
例题：
对于一个带电粒子在匀强磁场中作匀速圆周运动的过程，从出发点开始计时，求经过四分之一个周期洛伦兹力的总冲量。
方法一：根据动量定理，动量的变化量即为洛伦兹力冲量。$\sqrt{2} mv$，方向与该四分之一圆弧的弦垂直指向圆心。
方法二：由洛伦兹力方向始终与速度垂直，其冲量大小可通过累加计算。$\sum Bqv\Delta t = Bq x$，请注意这里的位移 $x$是矢量，大小即为带电粒子在四分之一圆周的弦长，方向与其垂直。那么，从圆上任一点出发，到圆上的任一点，洛伦兹力的总冲量大小均为 $Bq$ 乘以该两点间弦的长度，方向垂直于弦并指向圆心一侧。（洛伦兹力冲量最大的点在出发点对侧（直径）。）

二、洛伦兹力冲量的应用

第一题：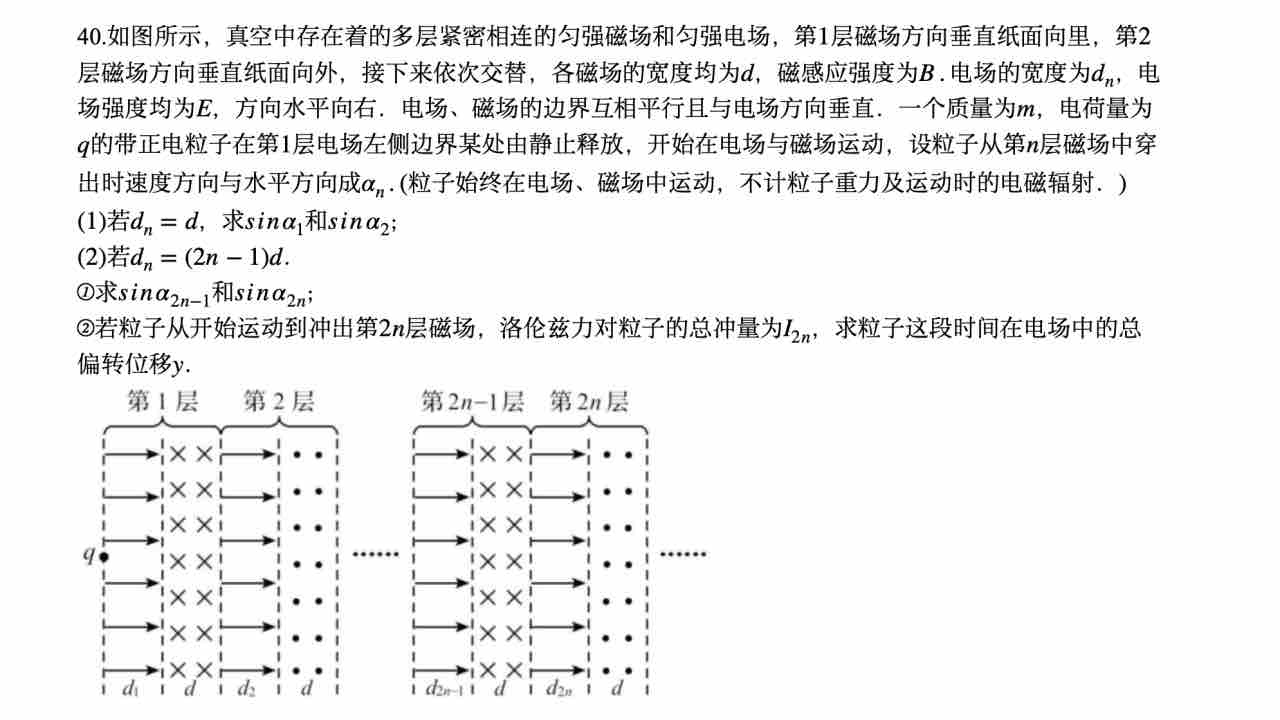

1）正弦值即为竖直分速度与速度的比值。其中竖直分速度可以使用动量定理求解，合速度可以通过动能定理计算。求解过程如下：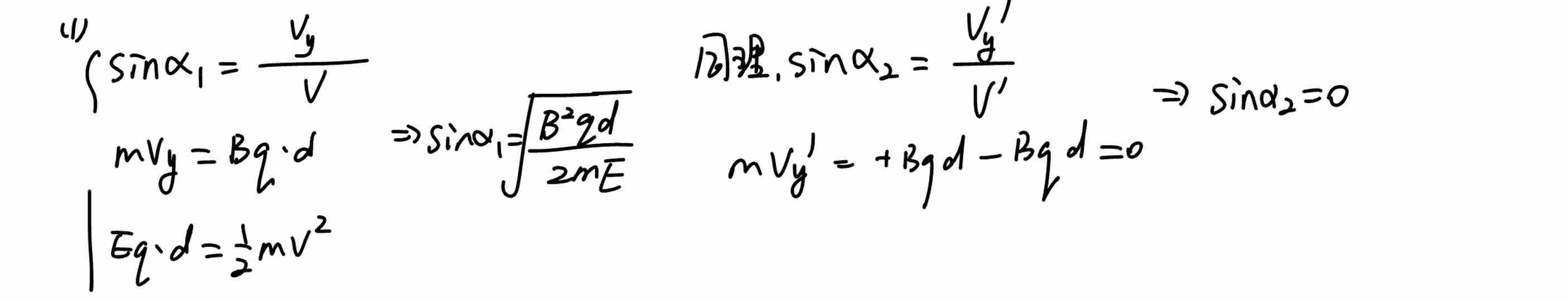

2）①问与（1）同理，使用动量定理的好处在于不用分析几何过程，带入对应的数据即可。求解过程如下：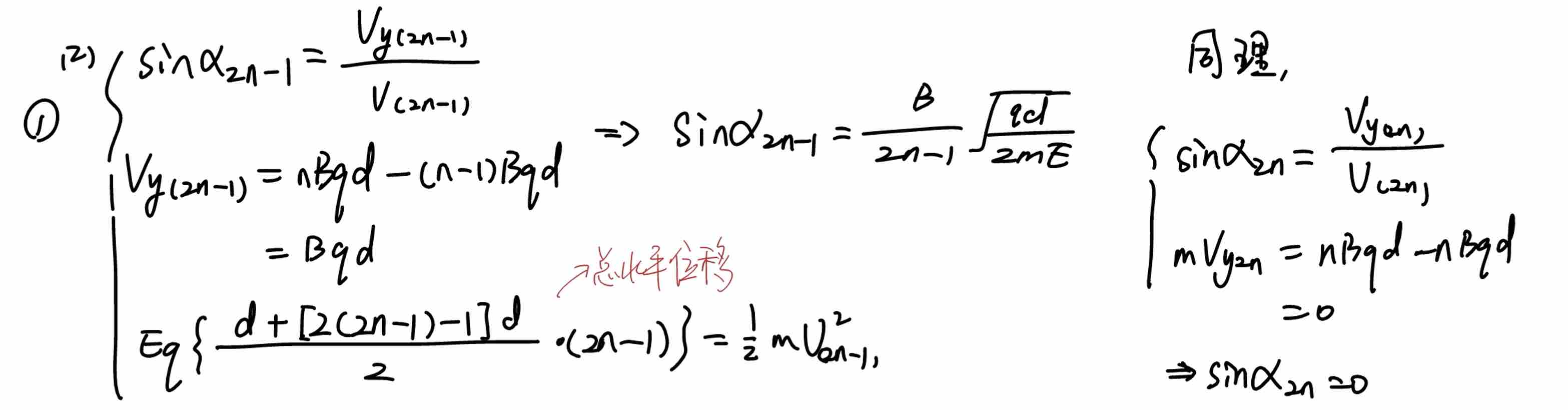

②问求解的是在电场中的总偏转位移。
根据（2）①问，由于磁场的偏转，进入奇数电场的速度方向是水平的，所以我们只需考虑在偶数电场中的偏转情况。
在偶数电场中，粒子的竖直速度均为$\frac{Bqd}{m}$，为匀速运动，所以竖直偏转位移为$\frac{Bqd}{m} \cdot t_{\text{偶}}$。
题目条件给了总冲量，可以用动量定理来求解电场中的总时间。
电场的宽度比例为1:3:5:7……，满足匀变速等时间间隔。但在偶数电场中，由于速度不沿着水平方向，时间会发生改变，但回到奇数电场中，继续等时间间隔，所以我们可以利用这一特点，求解奇数电场的时间$t_{\text{奇}}$。
求解过程如下：

那么，在磁场中的偏转位移是否可根据$I_{2n}$求？由于磁场的方向发生变化，使用竖直方向动量定理可能不行。这个问题目前还需要进一步思考。

第二题：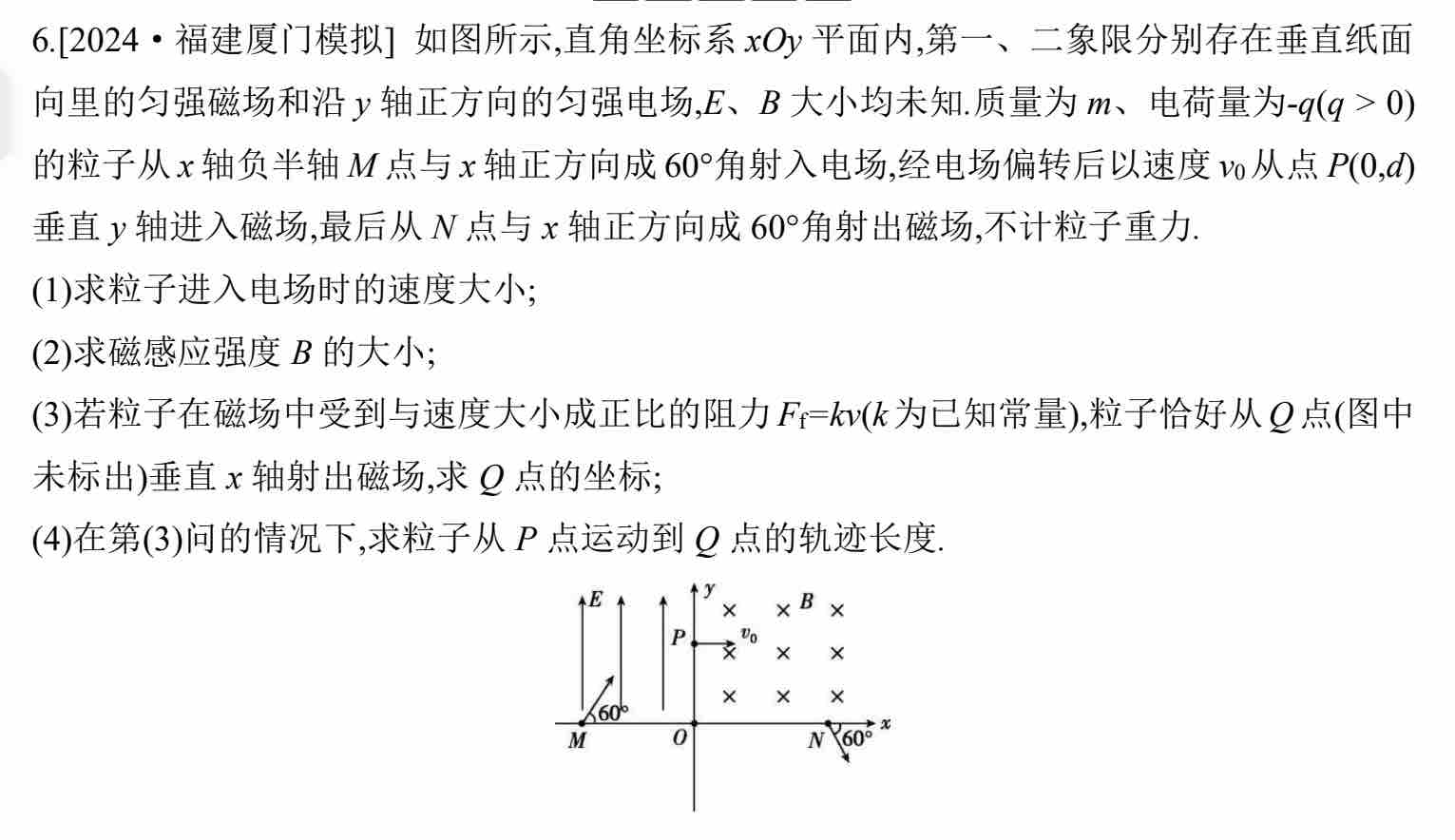

（1）（2）问为常规问题，比较简单，（3）问考察了单一方向动量定理的使用，也比较常规。亮点在（4）问：求解轨迹长度，使用了沿着轨迹切线方向的动量定理，这个方向上仅受阻力，可以求解轨迹长度，求解过程如下：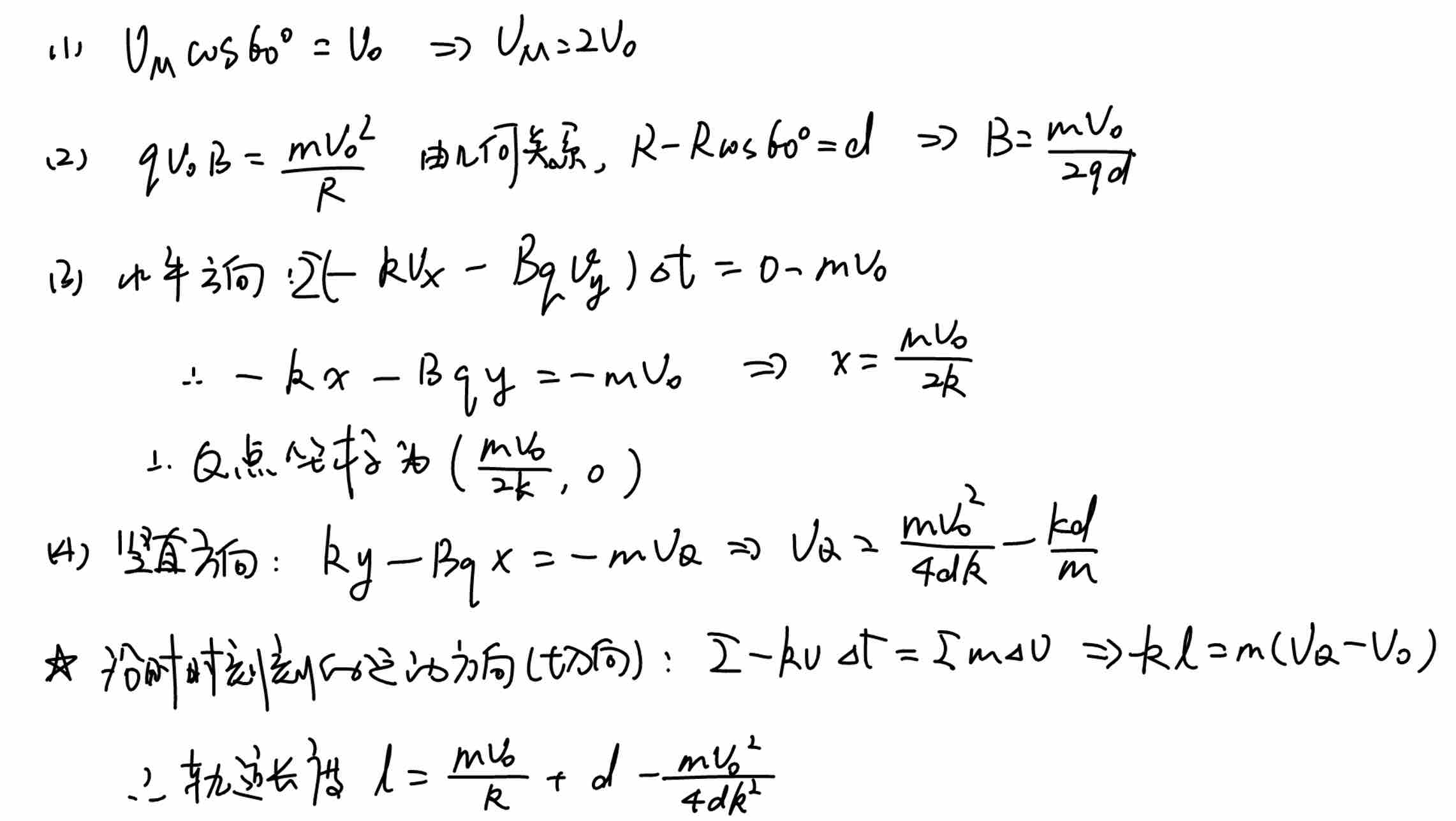

JQX|Jin

【下期预告】
从散度,旋度到麦克斯韦方程组，下期seminar将与大家共同探索物理中最迷人的推导之一:真空介电常数和真空磁导率与光速之间的联系。