七 10
JQX/进取芯 席明纳第10期(2025.5.30)


JQX|Xiao
两个质量分别为
 、
、 的两个星体,初始时静止,之间相距
的两个星体,初始时静止,之间相距 ,它们仅在万有引力作用下相互吸引,它们将在多久后相遇?
,它们仅在万有引力作用下相互吸引,它们将在多久后相遇?
方法一:用能量和积分推导
根据能量守恒: ,分离变量求积分得:
,分离变量求积分得: ,积分求时间(从
,积分求时间(从  到
到 ):
): ,解这个积分得到:
,解这个积分得到:
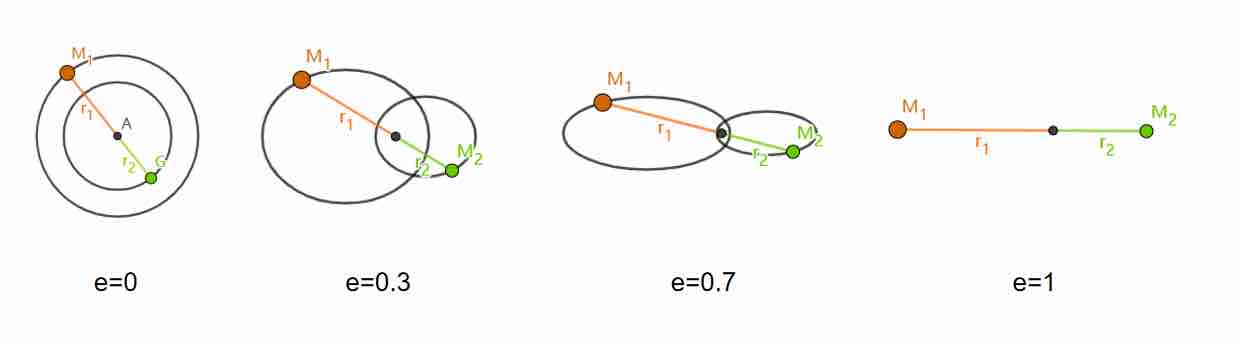
方法二:双星问题椭圆轨道:两个星体相互接近的过程可看作是在双星问题中,两个星体以系统质心为共同得焦点沿着各自得椭圆轨道运动,周期公式为 ,当离心率趋近于1,既半长轴趋近于半焦距时,椭圆退化为直线,即为本体模型,相遇时间为半个周期,带入公式得
,当离心率趋近于1,既半长轴趋近于半焦距时,椭圆退化为直线,即为本体模型,相遇时间为半个周期,带入公式得 。
。
方法三:等效为单体问题:两个星体得相对位置坐标为 ,以
,以 方向为正,对两个星体分别列牛顿第二定律:
方向为正,对两个星体分别列牛顿第二定律: 。相对加速度为:
。相对加速度为: ,引入约化质量
,引入约化质量 ,
, 。此时双体问题转为单体问题,可根据开普勒第三定律求周期,方法与上述方法相同。
。此时双体问题转为单体问题,可根据开普勒第三定律求周期,方法与上述方法相同。
方法四:引入等效质量。设想质心处有一个等效天体M,将 对
对 得引力等效为M对
得引力等效为M对 得引力。有:
得引力。有: ,其中
,其中 ,
, 为
为 到质心距离,r为两颗星体之间的距离。则此时可以在不引入双星周期公式和约化质量得情况下求得
到质心距离,r为两颗星体之间的距离。则此时可以在不引入双星周期公式和约化质量得情况下求得 到达质心作用时间,将这个问题带入第三种方法即可。
到达质心作用时间,将这个问题带入第三种方法即可。 ,时间为半个周期,解得
,时间为半个周期,解得 。
。
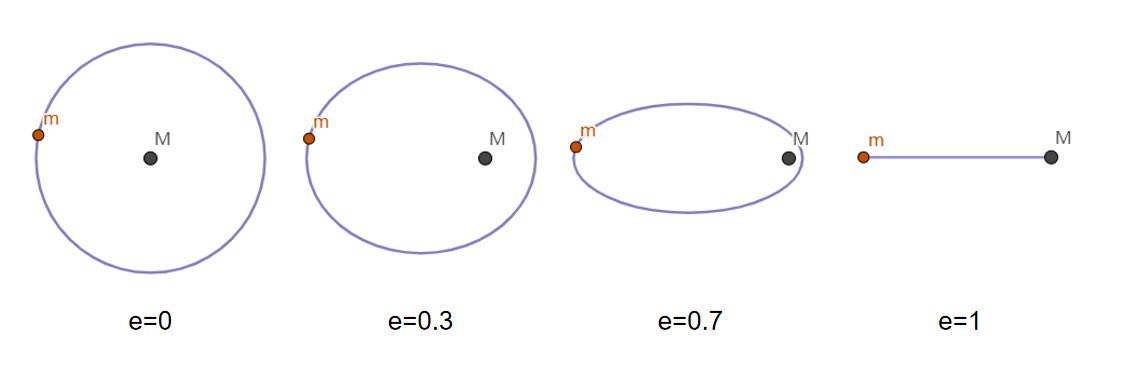
关于双星问题双椭圆轨道周期推导,可以将双星问题等效为质量为 得质点,在质量为M得引力作用下沿椭圆轨道运动得过程,即可得到双星轨道公式
得质点,在质量为M得引力作用下沿椭圆轨道运动得过程,即可得到双星轨道公式 。
。
On this day..
- #乱翻书《学以为己》 - 2025
- 岁月的苍老遮不住内心的年少 - 2016
- 成功,孩子要过几关? - 2004