JQX/进取芯 席明纳第23期(2025.12.25)

一、洛伦兹力的冲量
带电粒子在匀强磁场中运动时,所受洛伦兹力方向与速度方向时刻垂直。洛伦兹力的冲量可以通过累加进行计算。

其中, 为粒子从初始时刻到末时刻的位移矢量。该冲量的方向由叉积决定,始终垂直于位移矢量
为粒子从初始时刻到末时刻的位移矢量。该冲量的方向由叉积决定,始终垂直于位移矢量  与磁场
与磁场  所构成的平面,即同时垂直于
所构成的平面,即同时垂直于  和
和  。其大小为
。其大小为  ,
,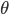 为
为  与
与  的夹角。
的夹角。
例题:
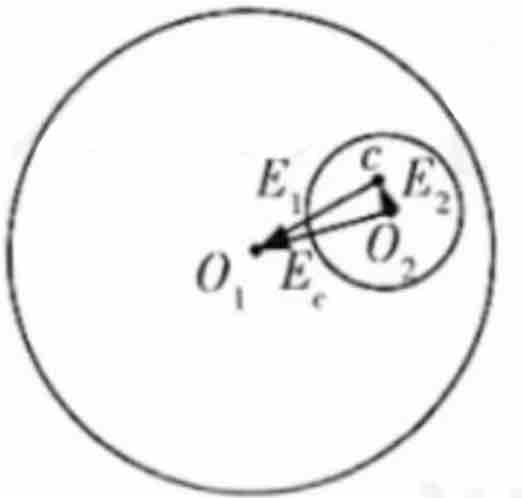
对于一个带电粒子在匀强磁场中作匀速圆周运动的过程,从出发点开始计时,求经过四分之一个周期洛伦兹力的总冲量。
方法一:根据动量定理,动量的变化量即为洛伦兹力冲量。 ,方向与该四分之一圆弧的弦垂直指向圆心。
,方向与该四分之一圆弧的弦垂直指向圆心。
方法二:由洛伦兹力方向始终与速度垂直,其冲量大小可通过累加计算。 ,请注意这里的位移x是矢量,大小即为带电粒子在四分之一圆周的弦长,方向与其垂直。那么,从圆上任一点出发,到圆上的任一点,洛伦兹力的总冲量大小均为
,请注意这里的位移x是矢量,大小即为带电粒子在四分之一圆周的弦长,方向与其垂直。那么,从圆上任一点出发,到圆上的任一点,洛伦兹力的总冲量大小均为 乘以该两点间弦的长度,方向垂直于弦并指向圆心一侧。(洛伦兹力冲量最大的点在出发点对侧(直径)。)
乘以该两点间弦的长度,方向垂直于弦并指向圆心一侧。(洛伦兹力冲量最大的点在出发点对侧(直径)。)
二、洛伦兹力冲量的应用
第一题:
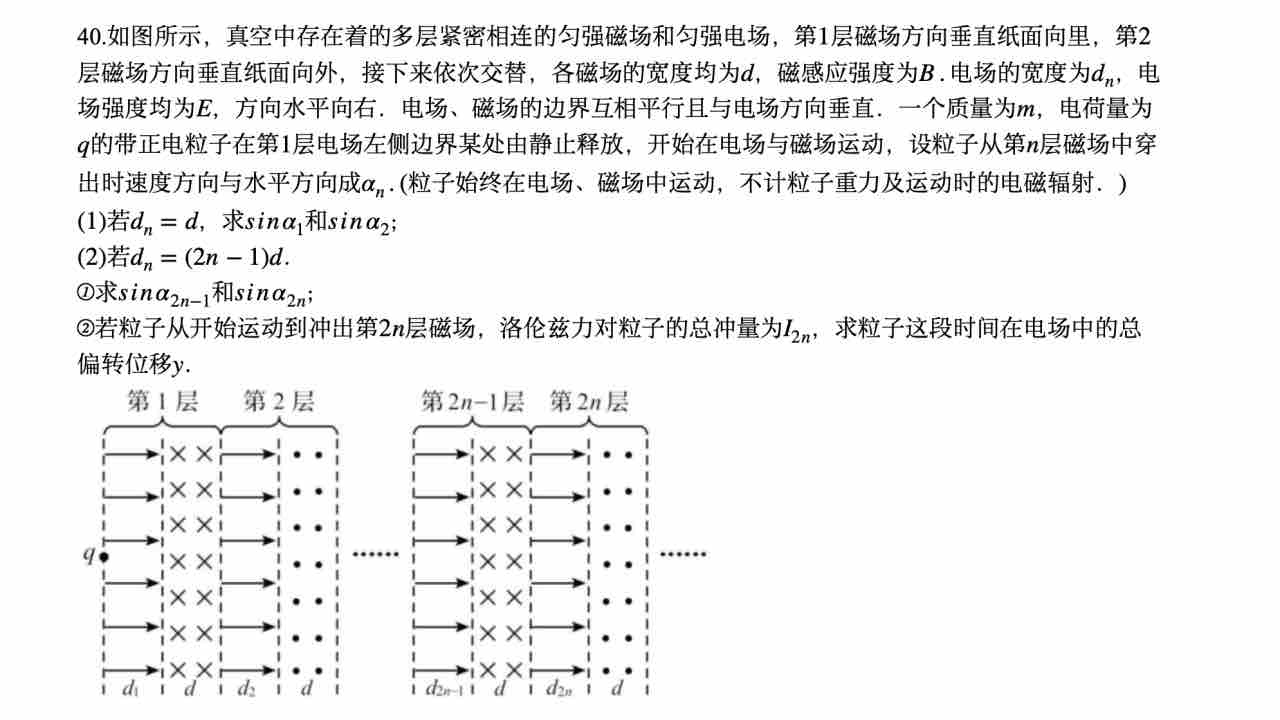
1)正弦值即为竖直分速度与速度的比值。其中竖直分速度可以使用动量定理求解,合速度可以通过动能定理计算。求解过程如下:
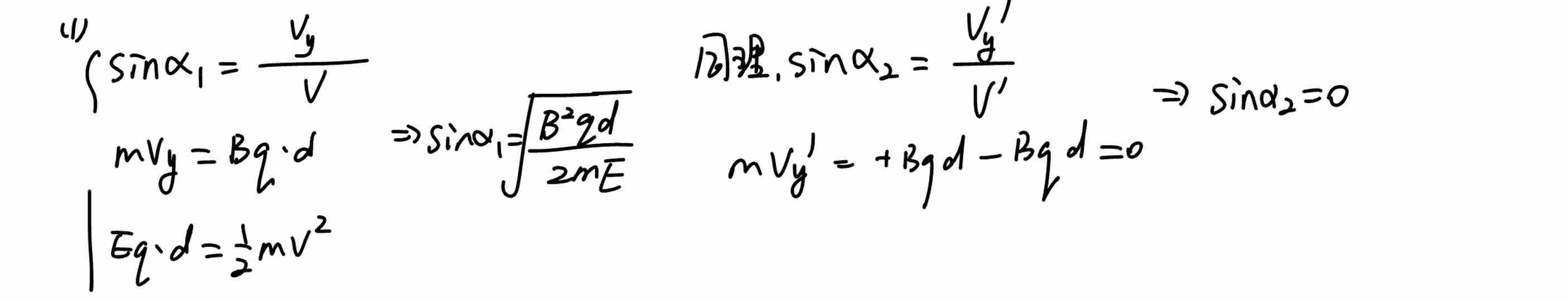
2)①问与(1)同理,使用动量定理的好处在于不用分析几何过程,带入对应的数据即可。求解过程如下:
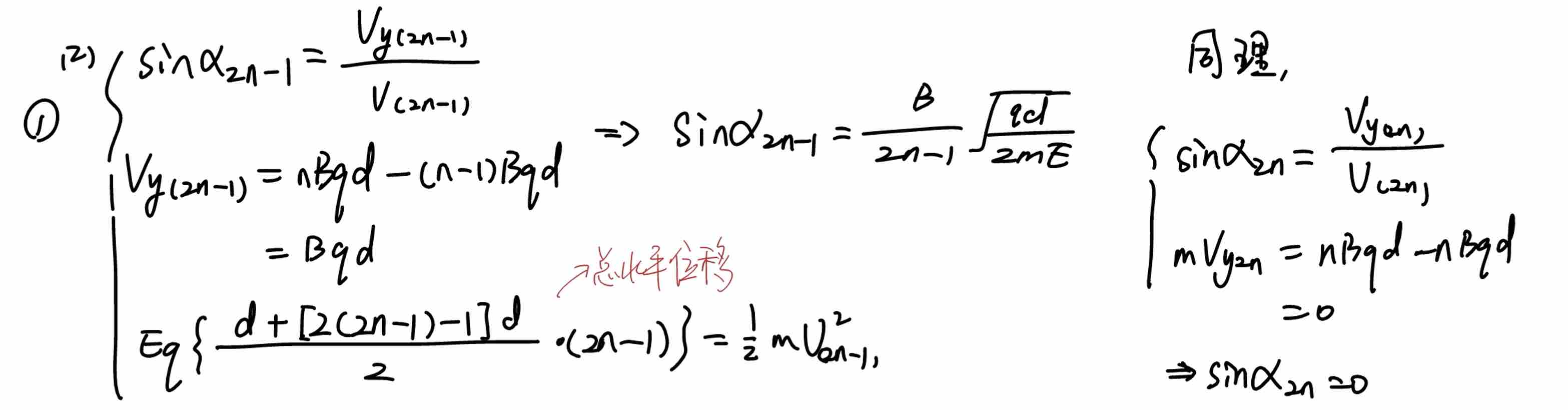
②问求解的是在电场中的总偏转位移。
根据(2)①问,由于磁场的偏转,进入奇数电场的速度方向是水平的,所以我们只需考虑在偶数电场中的偏转情况。
在偶数电场中,粒子的竖直速度均为 ,为匀速运动,所以竖直偏转位移为
,为匀速运动,所以竖直偏转位移为 。
。
题目条件给了总冲量,可以用动量定理来求解电场中的总时间。
电场的宽度比例为1:3:5:7……,满足匀变速等时间间隔。但在偶数电场中,由于速度不沿着水平方向,时间会发生改变,但回到奇数电场中,继续等时间间隔,所以我们可以利用这一特点,求解奇数电场的时间 。
。
求解过程如下:

那么,在磁场中的偏转位移是否可根据 求?由于磁场的方向发生变化,使用竖直方向动量定理可能不行。这个问题目前还需要进一步思考。
求?由于磁场的方向发生变化,使用竖直方向动量定理可能不行。这个问题目前还需要进一步思考。
第二题:
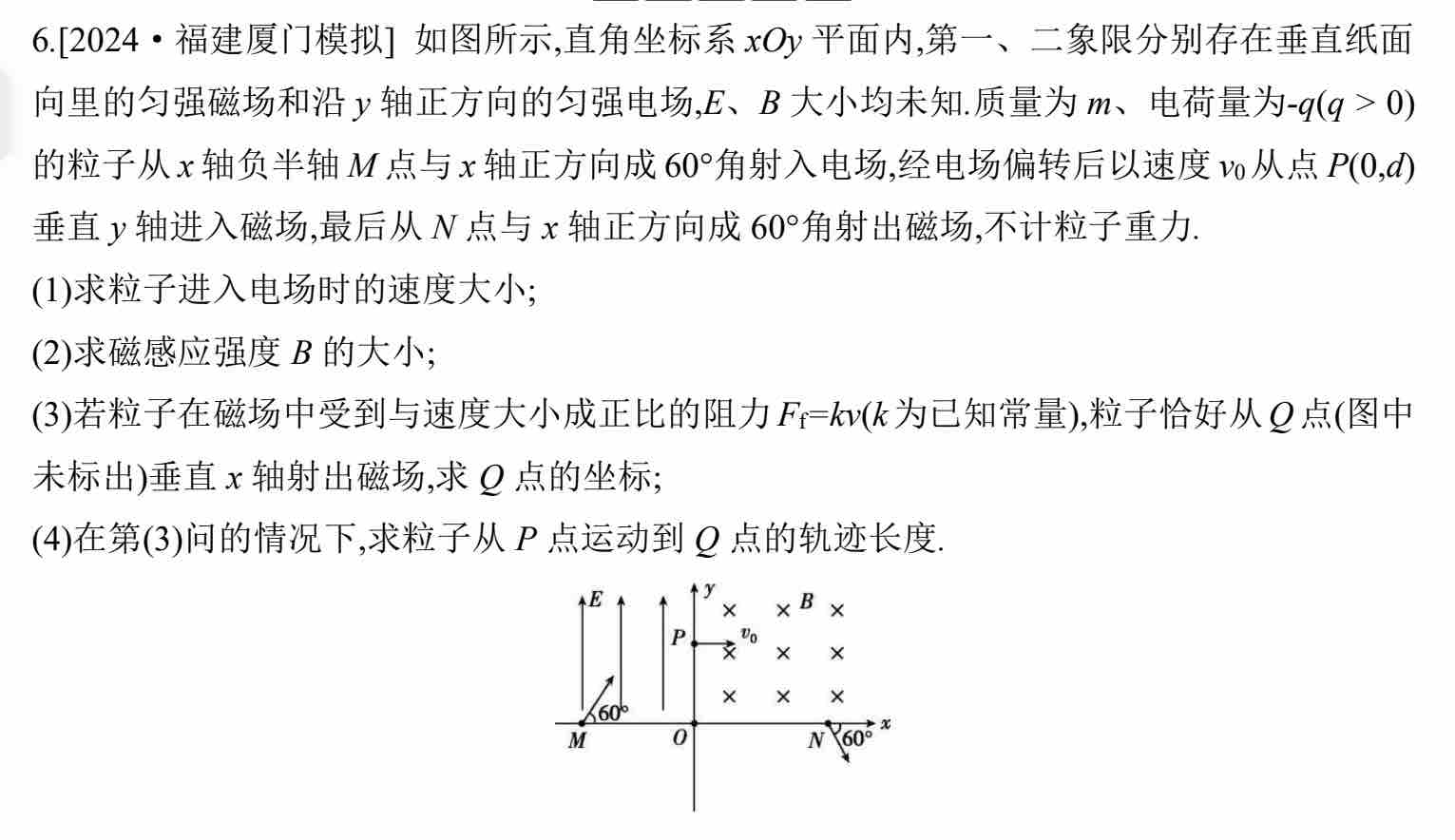
(1)(2)问为常规问题,比较简单,(3)问考察了单一方向动量定理的使用,也比较常规。亮点在(4)问:求解轨迹长度,使用了沿着轨迹切线方向的动量定理,这个方向上仅受阻力,可以求解轨迹长度,求解过程如下:
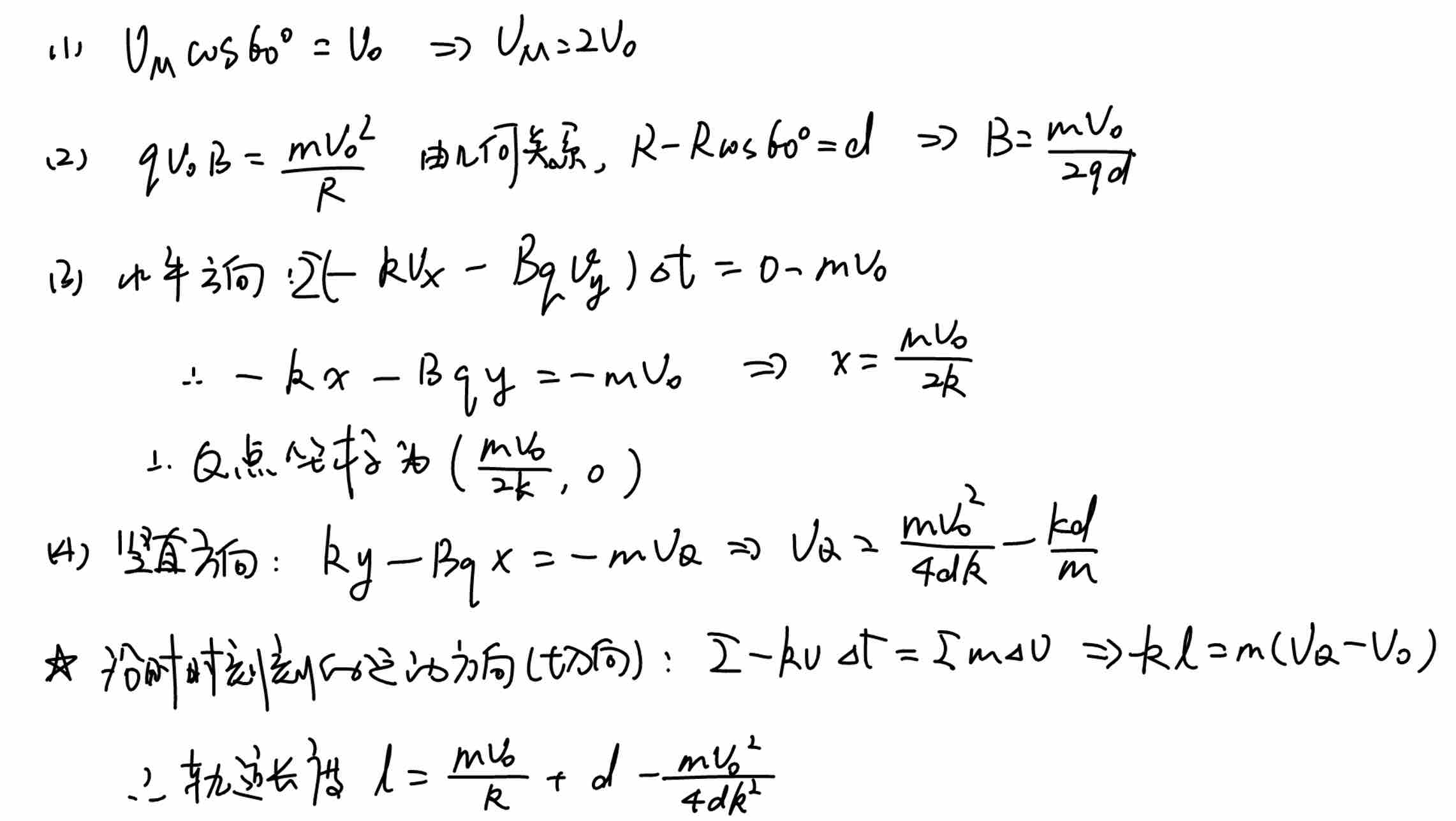

JQX|Jin
【下期预告】
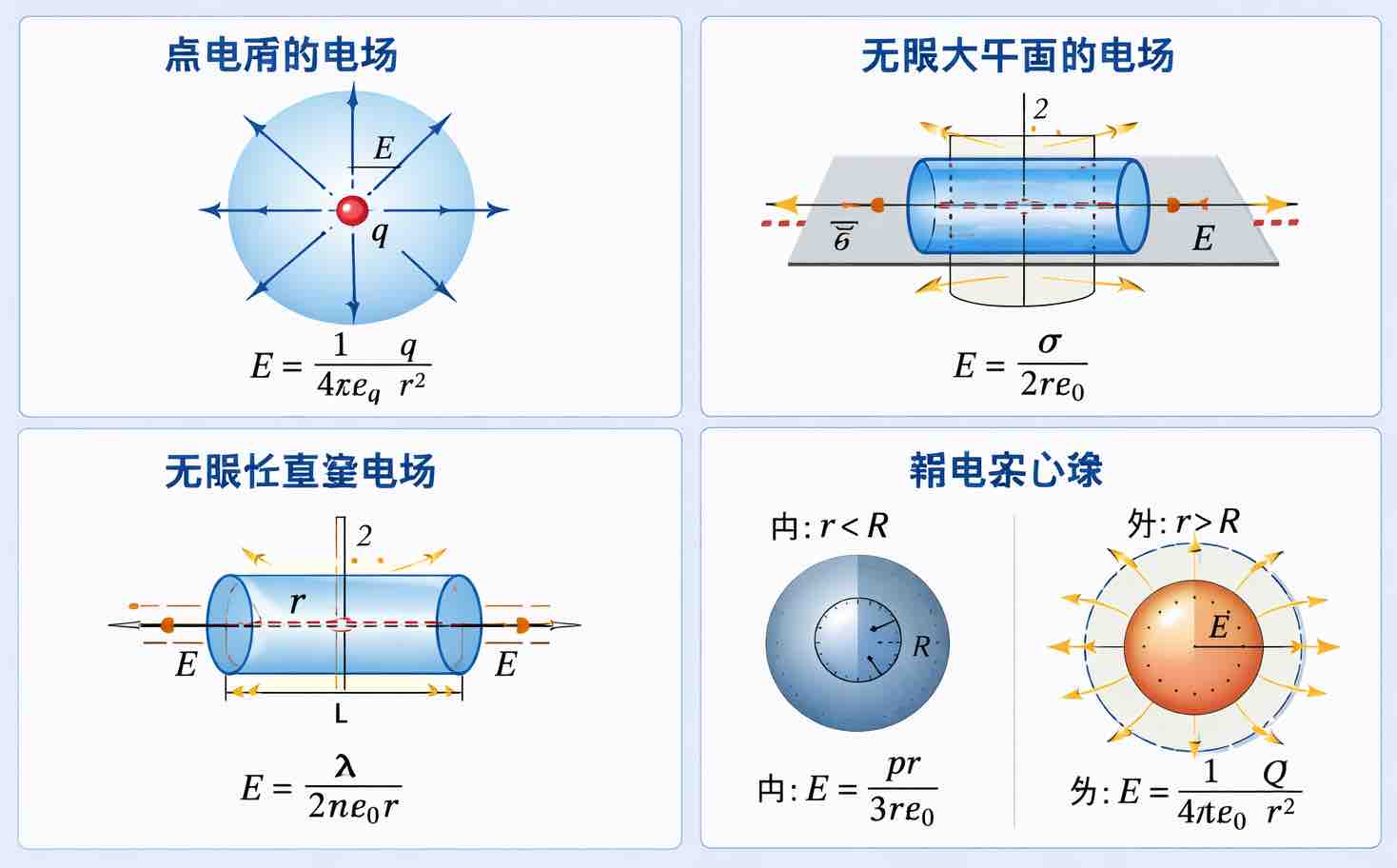
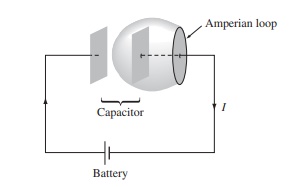
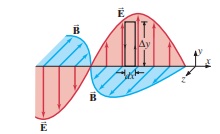
从散度,旋度到麦克斯韦方程组,下期seminar将与大家共同探索物理中最迷人的推导之一:真空介电常数和真空磁导率与光速之间的联系。


































![D(x,t) = A \sin \left[ \frac{2\pi}{\lambda} (x - vt) \right]](http://www.qiusir.com/wp-content/plugins/latex/cache/tex_83853f7dc9aad0392bdb04ba0532e292.gif)

































![k E_0 \cos(\dots) = - [-\omega B_0 \cos(\dots)]](http://www.qiusir.com/wp-content/plugins/latex/cache/tex_2641e3e0fe68ac7723c5b54d73fd904c.gif)


![- k B_0 \cos(\dots) = \mu_0 \epsilon_0 [-\omega E_0 \cos(\dots)]](http://www.qiusir.com/wp-content/plugins/latex/cache/tex_c11408563e7647597ad5026444fe0e59.gif)