速度关联和加速度关联
JQX/进取芯 席明纳第8期(2025.5.14)

在力学问题中,速度关联现象较为常见,而加速度是否也存在类似的关联规律呢?

JQX|Jin
一、绳 / 杆模型
一)例题
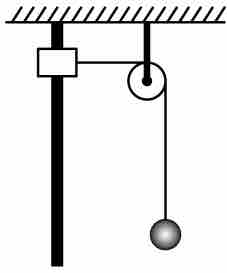
如图所示,物块套在固定竖直杆上,通过轻绳跨过定滑轮与小球相连,初始时刻物块与定滑轮等高。已知物块质量
 ,小球质量
,小球质量  ,杆与滑轮间的水平距离
,杆与滑轮间的水平距离  ,重力加速度
,重力加速度  ,且轻绳和杆长度足够,忽略一切摩擦与空气阻力。现将物块由静止释放,在其下落过程中,求解以下问题:
,且轻绳和杆长度足够,忽略一切摩擦与空气阻力。现将物块由静止释放,在其下落过程中,求解以下问题:1. 物块下降的最大距离
设物块下落的最大高度为
 ,此时小球上升的最大距离为
,此时小球上升的最大距离为  。根据几何关系可知:
。根据几何关系可知:
机械能守恒定律可得:

解得:

2. 系统动能最大时物块的动能
这里有两种方法:
1)写出动能与角度的表达式,进行数学方法求极值。
2)从物理意义上考虑,当系统的重力功率之和为
 时,系统动能达到最大值。
时,系统动能达到最大值。设物块速度为
 ,小球速度为
,小球速度为  ,根据速度关联关系可知:
,根据速度关联关系可知:
由重力功率关系可得:

对物块和小球组成的系统,运用机械能守恒定律求解动能最大值,可得动能最大值为:

3. 物块运动的最大速度
1)原答案解析
答案寻找了一个特殊位置:当物块的速度最大时,加速度为
 ,由于物块和小球被绳牵连,沿绳方向的加速度大小相等,小球的加速度也为
,由于物块和小球被绳牵连,沿绳方向的加速度大小相等,小球的加速度也为  ,所以物块和小球同时达到最大速度,分别为
,所以物块和小球同时达到最大速度,分别为  和
和  。分别对物块和小球列平衡方程得:
。分别对物块和小球列平衡方程得:

由(1)式可求得:
 则:
则:
如图3所示,由物块和小球沿绳方向的速度大小相等得:

由系统的机械能守恒:

联立(2)(3)(4)式解得:


2)对原答案的质疑
原答案认为,既然沿绳方向的速度大小时刻相等,沿绳方向的加速度大小一定会相等,并且找到了一个特殊位置,满足两个物体加速度同时为  。但是,这个理论靠得住脚吗?
。但是,这个理论靠得住脚吗?
设物块的速度为  ,小球的速度为
,小球的速度为  ,二者速度关系为:
,二者速度关系为:
对该速度关系两边求导,可得:
我们发现,不存在两个物体加速度同时等于0的情况。原答案解析是有错误的。
当物块的速度最大时  ,则有
,则有 
对物块有 
对小球有 
对物块与小球组成的机械能守恒,可得  其中
其中  ,
,
联立解得 
二)讨论:加速度关联(沿绳方向加速度相等)满足的条件
1. 速度为零
2. 角速度为零
3.  趋近于
趋近于 
我们也可以进一步推导公式,发现多出一项即为绳的向心加速度。所以,如果出现旋转,在加速度关联时,就要加上向心加速度这一分量。
三)速度关联的三种推导方法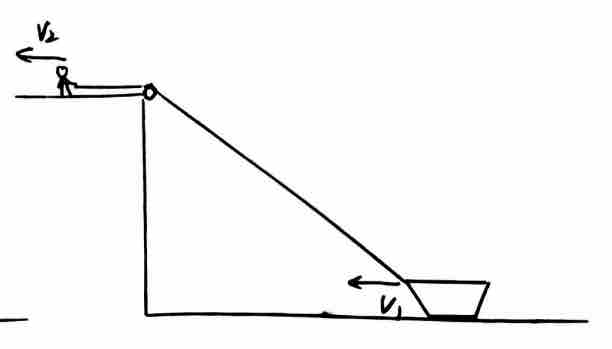
在绳连接船的系统中,根据沿绳方向加速度相等,可得: 其中
其中  为绳与水平方向的夹角。
为绳与水平方向的夹角。
1. 求导法
设船与岸边距离为  ,绳长为
,绳长为  ,定滑轮高度为
,定滑轮高度为  ,根据勾股定理可得:
,根据勾股定理可得:
对时间  求导,得到:
求导,得到:
其中  表示船的速度
表示船的速度  ,
, 表示人收绳的速度
表示人收绳的速度  。可得到:
。可得到:
结合几何关系可推导出:
2. 微元法
取极短时间  ,此时绳转过角度
,此时绳转过角度  。过船所在位置
。过船所在位置  作绳初始位置
作绳初始位置  的垂线
的垂线  ,由于
,由于  ,可近似认为
,可近似认为  。
。
人收绳长度:
船运动距离:
根据  ,有:
,有:

又因为  ,将上述关系代入可得:
,将上述关系代入可得:
约去  ,得到:
,得到:
3. 功率法
考虑到绳为轻质绳,不储存能量,这意味着人拉绳的瞬时功率时刻等于绳对船的作用力的瞬时功率。根据功率公式  ,可列出等式:
,可列出等式:
等式两边拉力  相同,化简后得到:
相同,化简后得到:
拓展例题:虚功原理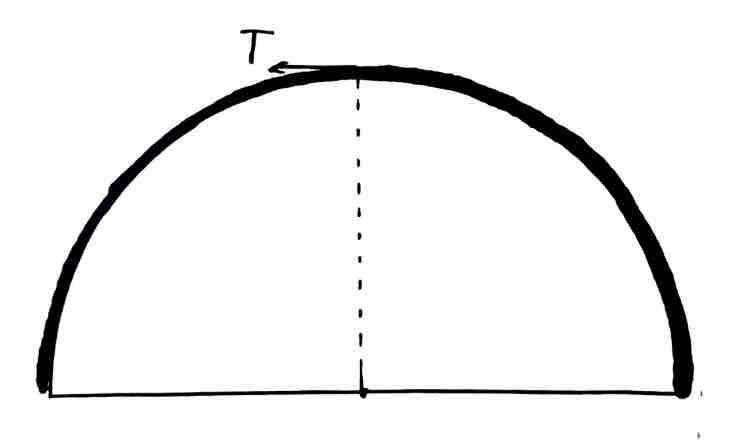
如图所示,一条线密度为  的均匀铁链,静止放置于半径为
的均匀铁链,静止放置于半径为  的光滑半圆形台上。铁链两侧对称下垂且恰好落在半圆末端。试求解铁链在最高点处的拉力
的光滑半圆形台上。铁链两侧对称下垂且恰好落在半圆末端。试求解铁链在最高点处的拉力  。
。
提示:可以认为铁链向左移动很小一段,相当于拉力做功将末端的一小段质量搬运到了最高点。

二、接触模型
1.在接触模型中,两物体接触处的速度关联通常将接触点处的速度沿接触面切线方向和垂直于接触面方向分解,由于两物体始终保持接触,垂直于接触面方向的分速度大小相等。
而在加速度关联方面,垂直于接触面方向的加速度存在关联关系,具体推导过程与绳杆模型相同。


其中:
 为相对速度,
为相对速度, 为曲率半径。
为曲率半径。
若接触面是平面,则垂直于接触面方向的加速度相同。若接触面是曲面,还需考虑向心加速度对加速度关联的影响。这个加速度计算时,速度应为接触点相对于接触面的加速度,半径应为曲率半径。
2. 相对向心加速度的使用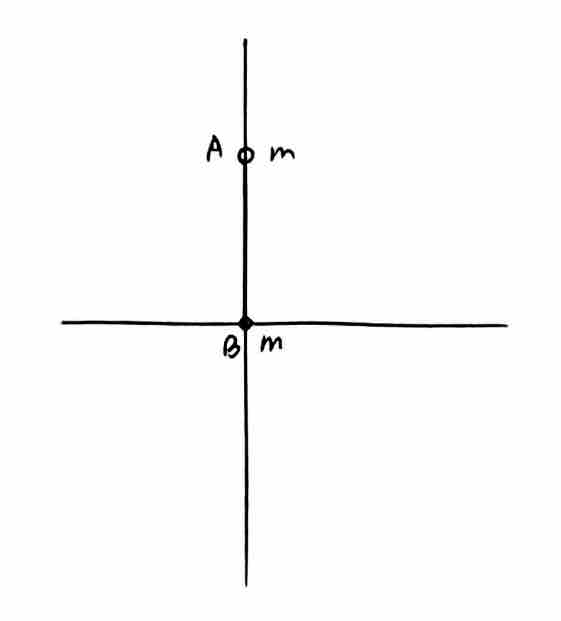
在高中物理中,我们利用向心加速度计算时,带入的速度均为相对于圆心的速度(因为不相对于圆心,也不是圆周运动了)。
例题:两个固定的光滑杆十字放置但不接触,两个质量为  的
的  、
、 两球套在杆上并用铰链通过另一长为
两球套在杆上并用铰链通过另一长为  的直杆相连。初始位置如图所示,轻微扰动
的直杆相连。初始位置如图所示,轻微扰动  球后,求
球后,求  球的最大速度。
球的最大速度。
方法一:
速度关系:
机械能守恒:
联立解得:
通过求导求极值,可得当  时,
时, 取得最大值。
取得最大值。
方法二:相对向心加速度(帅)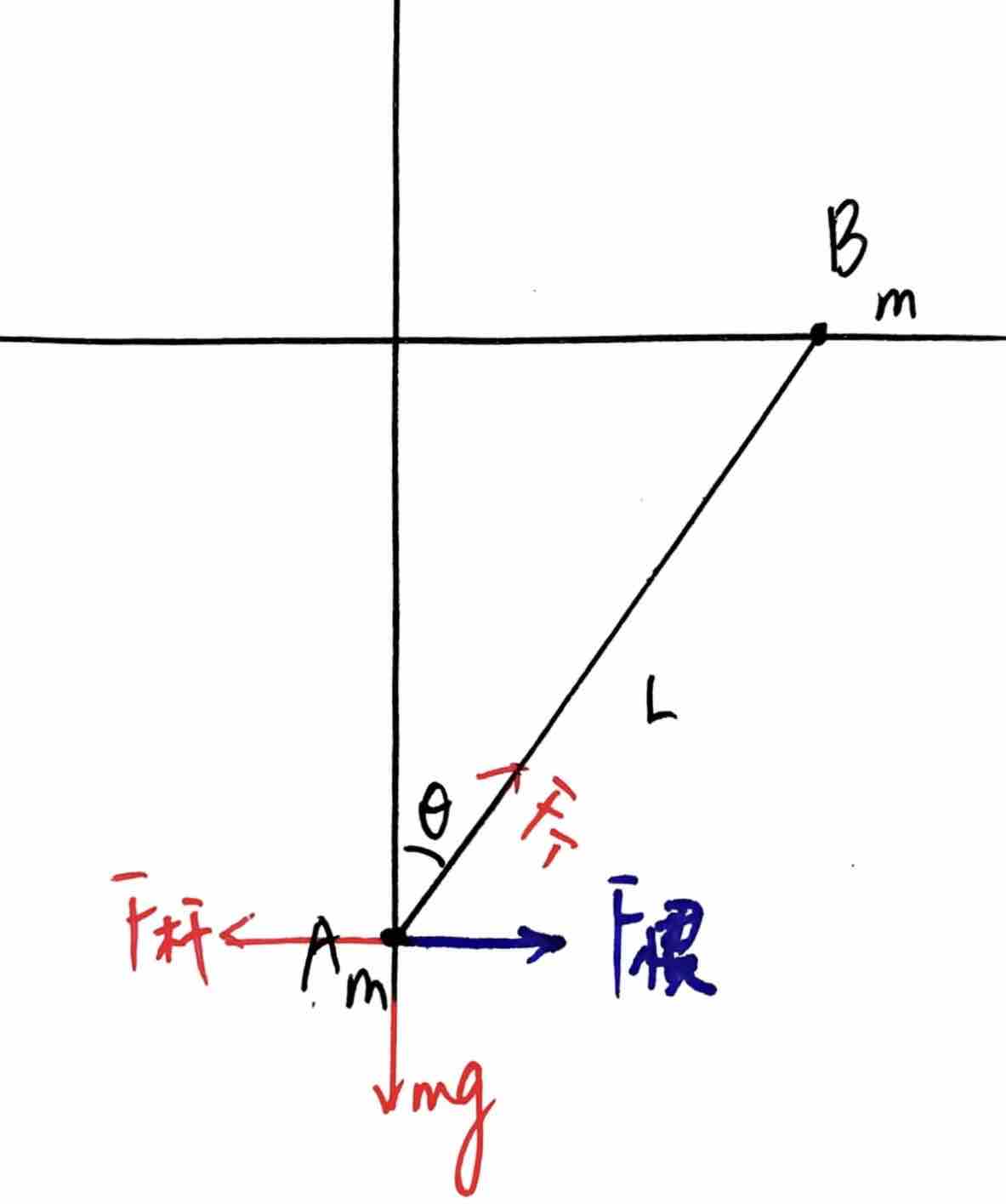
在实际教学中,计算杆上力的时候,经常使用相对运动的方法列圆周运动。本题可以以B球为参考系,则A球相对B球做圆周运动。
那么在A球受力分析时,要引入惯性力(B球的ma),这个力恰好与A球所受杆的力大小相等方向相反(惯性参考系使用质点系牛二分析水平方向),这两个力合力为零。
所以沿杆方向的力只有杆力和重力分力:
速度最大时,A球竖直方向加速度为0,有
再结合机械能守恒和速度关系:  、
、 
解得  ,结果与方法一相同。
,结果与方法一相同。
三、动滑轮模型
一)例题分析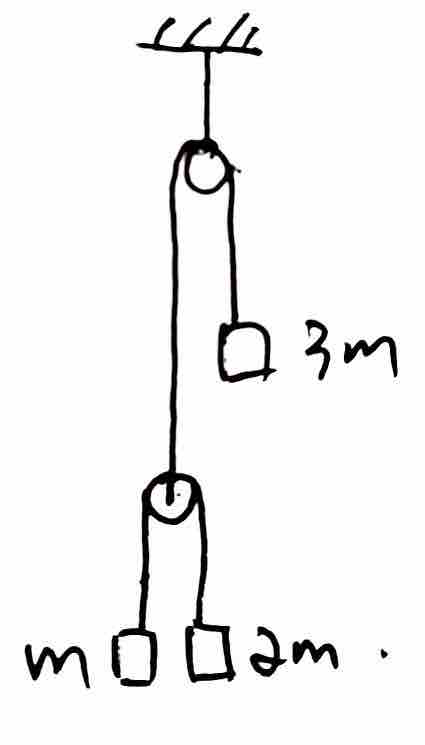
如图,三个已知质量的物块通过轻绳、轻滑轮连接,不计一切阻力,由静止释放,已知重力加速度  ,求三者加速度大小各是多少。
,求三者加速度大小各是多少。
设三个物块质量分别为  、
、 、
、 ,加速度分别为
,加速度分别为  、
、 、
、 ,绳子拉力分别为
,绳子拉力分别为  、
、 。
。
根据牛顿第二定律对三个物块分别列式:
对于质量为  的物块:
的物块:
对于质量为  的物块:
的物块:
对于质量为  的物块:
的物块:
同时,根据滑轮的力学关系有:
根据物块间加速度关联,有:![a_1 - (-a_3) = -[a_2 - (-a_3)]](http://www.qiusir.com/wp-content/plugins/latex/cache/tex_852f0140fc2db328aa97dafea841ee87.gif)
联立求解后,可得:
易错点:
1. 左侧滑轮的加速度关联(换参考系)问题。
2. 滑轮的力学关系。
二)绳拉船问题加滑轮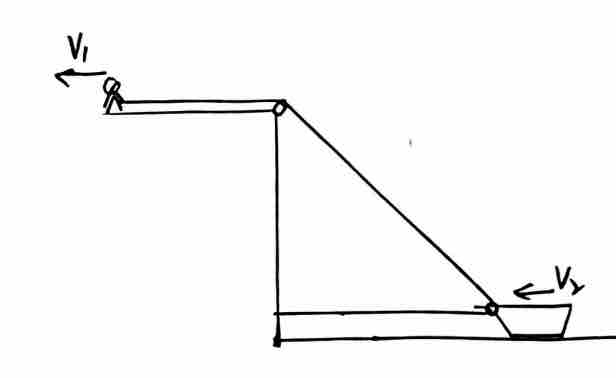
如果将绳拉船问题的船加上一个滑轮,另一端水平连接到岸边,如黑板左中图所示。那么,这个情况下的速度关联如何?
方法一:求导法



对时间求导,
方法二:功率法

方法三:微元法

从物理意义上来看,滑轮的引入在原有速度关联的基础上,增加了水平绳子缩短的速度。
【下期预告】邀请高一六班刘而行同学交流“非惯性参考系与惯性力”···
On this day..
- 人间值得 - 2024
- 罗素自选文集* - 2022
- 时间简史 - 2020
- GGB3D - 2015
- 夜卧观飞雪 晨起踏槐花 - 2011
- 夏天来了,春天的那些花儿谢了 - 2010
- 谁是弱者? - 2008
- 《乐学歌》 - 2006
- 没有哪件事像你想象的那么简单 - 2004
- 作为教师的不易 - 2004