高中电路的进阶定理及应用
JQX/进取芯 席明纳第12期(2025.7.9)


JQX|Jin
一、基尔霍夫定律
可以理解为电路中 “节点电流” 和 “回路电压” 的两条规则
电流定律:电路中任何一个节点,流进去的电流总和等于流出来的电流总和。
电压定律:电路中任何一个闭合回路,电源提供的总电压等于回路中所有电阻 “消耗” 的电压之和(电流流过电阻,降电势)。
二、叠加定律
多个电源同时给电路供电时,某段电路的电流(或电压),等于每个电源单独供电时(其他电源短路)在这段电路产生的电流(或电压)加起来的结果(比如两个电池一起工作,效果等于先算第一个电池的电流,再算第二个的,最后相加)。
三、戴维南定理
一个复杂的含电源电路,对外接的用电器来说,可以简化成一个 “等效电池”:这个等效电池的电压等于电路两端不接用电器时的电压(开路电压),内阻等于把电路里所有电源断路(我们高中一般都是恒压电源,如果是恒流源,需要将电源短路)后,两端的等效电阻。
例题分析
例 1:求通过三个电阻的电流
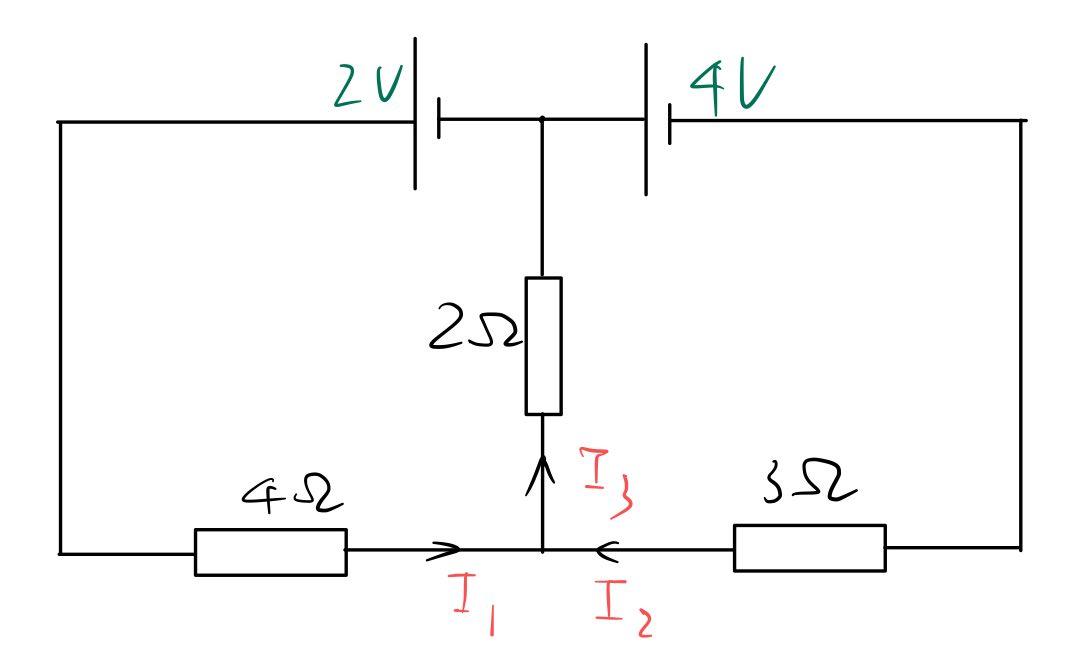
法一:基尔霍夫定律



解得
 ,
, ,
,
法二:叠加定律(以计算
 为例)
为例)若将
 电源短路,有:
电源短路,有:
若将
 电源短路,有:
电源短路,有:
则
 ,结果一致。
,结果一致。
例 2:求通过电阻的电流
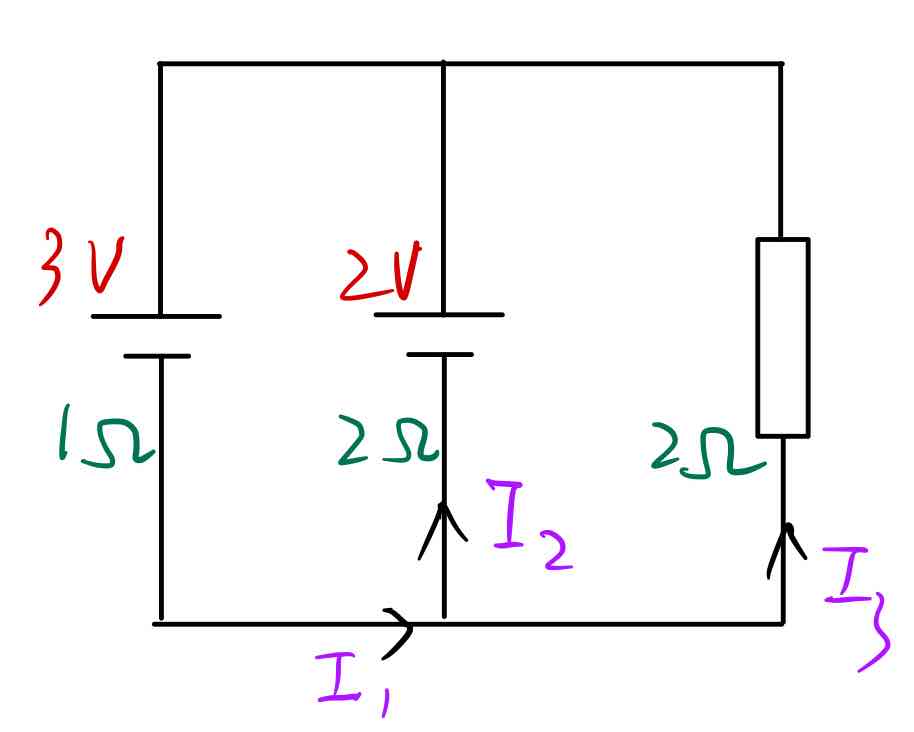
法一:基尔霍夫定律



解得  ,
, ,
,
法二:叠加定律
略,将电源短路,但内阻保留。
例 3:分析电路三个电阻的连接关系
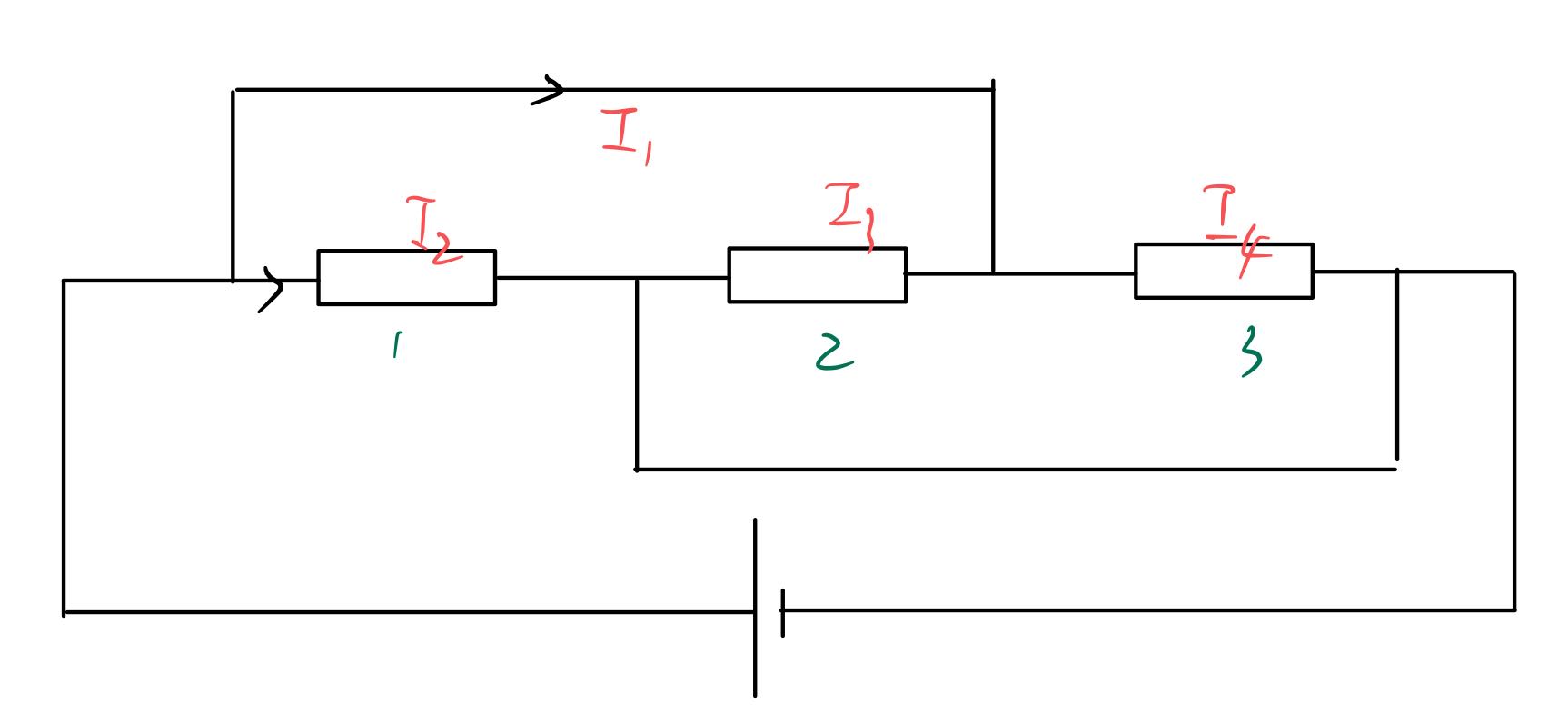
法一:电势点法
如黑板图,同一导线电势相等,则每个电阻都是在 1、2 电势之间,为并联关系。
法二:移动负载法(捏点)
把最上方的导线捏成一个点,中间的电阻自然相当于移动到两侧电阻中间与之并联,为并联关系。
法三:基尔霍夫定律
最下层:
1、2 回路:
2、3 回路:
推导得  ,可知为并联关系。
,可知为并联关系。
例 4:不平衡电桥的计算
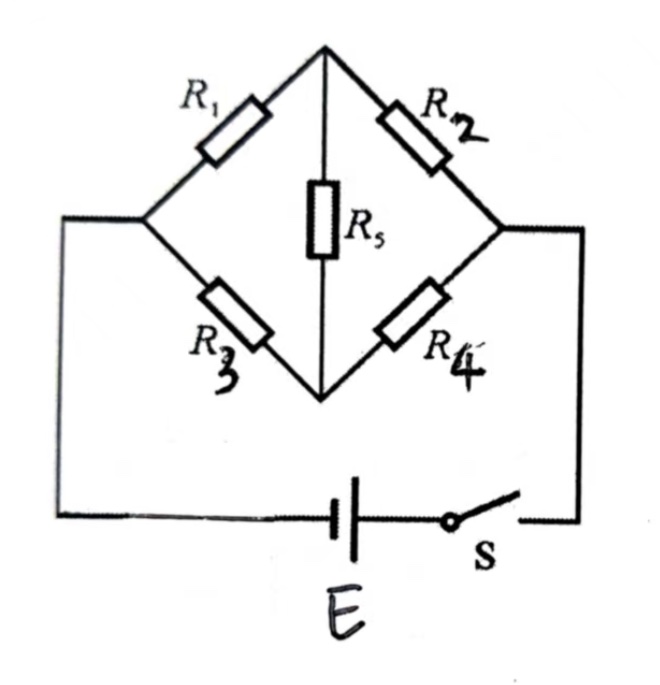
求流过  的电流大小
的电流大小
法一:基尔霍夫定律
电流关系方程


电压关系方程



解得流过  的电流为
的电流为 
法二:戴维南定理
我们可以将  两端断开,把其他所有部分想象成一个等效电源,这样,我们就能把电路简化为电源和
两端断开,把其他所有部分想象成一个等效电源,这样,我们就能把电路简化为电源和  的串联。
的串联。
按照戴维南定理,我们将  断开后,
断开后, 两端的电压即为等效电源的电动势,计算可得
两端的电压即为等效电源的电动势,计算可得  。再将电源短路(保留内阻),剩余的电阻(
。再将电源短路(保留内阻),剩余的电阻( 、
、 串联与
串联与  、
、 串联后并联)即为等效电源的内阻,
串联后并联)即为等效电源的内阻, 。
。
这样,我们可以直接将  串入这个等效电阻中,求得电流为
串入这个等效电阻中,求得电流为  。
。
拓展例题(2025年高考物理 甘肃卷压轴题)
在自动化装配车间,常采用电磁驱动的机械臂系统,如图, 、
、 为两条足够长的光滑平行金属导轨,间距为
为两条足够长的光滑平行金属导轨,间距为  ,电阻忽略不计。导轨置于磁感应强度大小为
,电阻忽略不计。导轨置于磁感应强度大小为  ,方向垂直纸面向里的匀强磁场中,导轨上有与之垂直并接触良好的金属机械臂 1 和 2,质量均为
,方向垂直纸面向里的匀强磁场中,导轨上有与之垂直并接触良好的金属机械臂 1 和 2,质量均为  ,电阻均为
,电阻均为  。导轨左侧接有电容为
。导轨左侧接有电容为  的电容器。初始时刻,机械臂 1 以初速度
的电容器。初始时刻,机械臂 1 以初速度  向右运动,机械臂 2 静止,运动过程中两机械臂不发生碰撞。系统达到稳定状态后,电流为零,两机械臂速度相同。
向右运动,机械臂 2 静止,运动过程中两机械臂不发生碰撞。系统达到稳定状态后,电流为零,两机械臂速度相同。
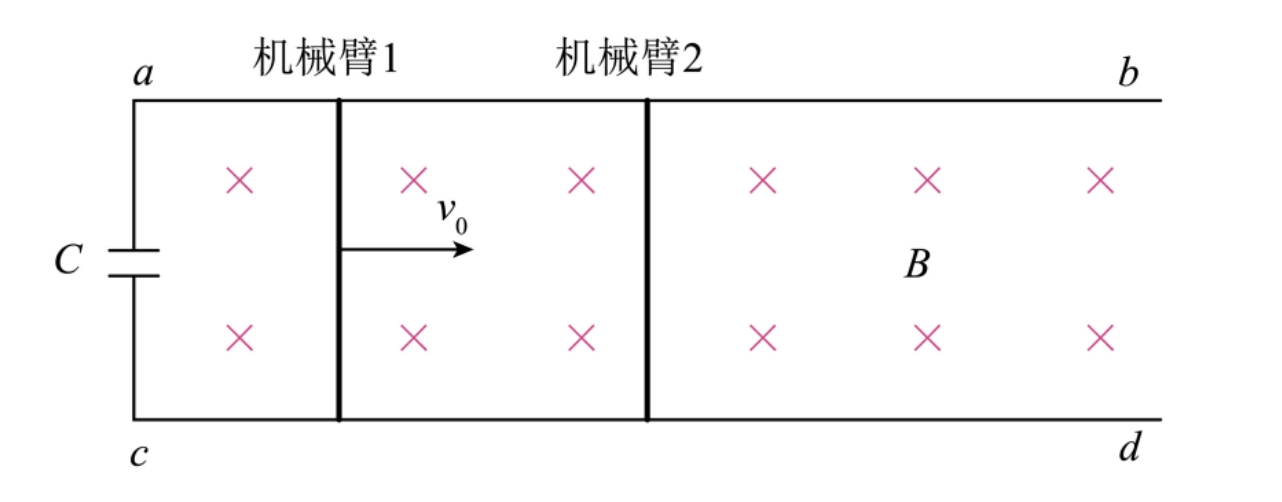
(1) 求初始时刻机械臂 1 的感应电动势大小和感应电流方向;
(2) 系统达到稳定状态前,若机械臂 1 和 2 中的电流分别为  和
和  ,写出两机械臂各自所受安培力的大小;若电容器两端电压为
,写出两机械臂各自所受安培力的大小;若电容器两端电压为  ,写出电容器电荷量的表达式;
,写出电容器电荷量的表达式;
(3) 稳系统达到稳定状态后两机械臂的速度。若要两机械臂不相撞,二者在初始时刻的间距至少为多少?
解析:
(1)  ,感应电流方向沿机械臂 1 向上
,感应电流方向沿机械臂 1 向上
(2)  、
、 ,
,
(3) 达到稳定  时,两机械臂的速度相同,产生的感应电动势与电容器的电压相等,回路中没有电流
时,两机械臂的速度相同,产生的感应电动势与电容器的电压相等,回路中没有电流 
法一:
可将电容等效为质量为  的单杆,三杆动量守恒,
的单杆,三杆动量守恒,
可得两机械臂的速度为  ,方向向右。
,方向向右。
法二:
从开始到最终稳定的过程中,对机械臂 1 和机械臂 2 分别根据动量定理有  ,
,
即  ,
, ,
,
联立解得  。
。
关键是最短距离的求法,最短距离需要知道相对位移。
根据基尔霍夫定律,任意时刻有 
即 
有 
其中  ,
, ,
, 
即 
联立解得稳定时的速度和两棒间初始距离的最小值为 
最后,我们来尝试计算一道有趣的等效电阻题:
如做黑板中下部图片所示,某电路由六根相同的导体组成立方体,电流从0流入。如果从1流出,那么回路电阻为多少? 如果从2/3流出,等效电阻又分别为多少?
On this day..
- 求师得数位学习推介 - 2023
- 东东弗斯 - 2022
- 一只特立独行的猪 - 2019
- 糟糕事是时机不当的结果 - 2017
- 别怕讨论天真的问题 - 2009
- 最漂亮的物理实验TOP10 - 2008
- 真爱你的孩子 - 2005
- 精神和物质的损失你选择什么? - 2004