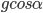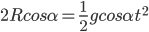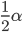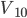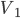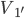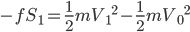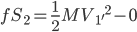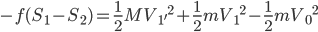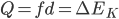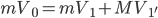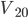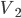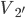斜面是高中物理中经常用到的模型,这里尝试着整理一些基础的题目。希望静态能够有帮建立动态,也希望能扫清一些关键性结论的认知障碍。
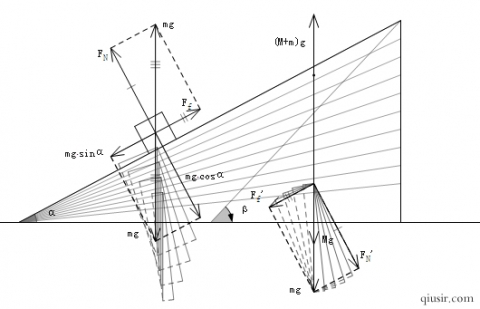
水平地面上静止的斜面上,一物体沿斜面匀速下滑。对滑块受力分析(重力、弹力、摩擦力)。匀速运动,所以受力平衡。
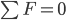
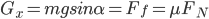
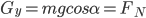 ,不难得出:
,不难得出: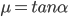 (如果摩擦系数比这大或小呢)
(如果摩擦系数比这大或小呢)
对斜面的受力分析,关键是理解弹力和摩擦力的反作用力的合力大小为mg(旋转了180°)。当然也可以用整体法,系统质心匀速下降,仍属平衡态,地面支持力为(M+m)g。斜面并无水平方向运动趋势,自然不受地面的摩擦力了。
如果斜面的角度变化,图中给出重力的分解图示以及对斜面受力情况,配合着代数式理解。当然如果物体静止在斜面上,受其情况同上,只不过原来的滑动摩擦力变为静摩擦力。
如果摩擦系数
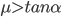 且无初速度释放,受力情况同上。如果摩擦系数
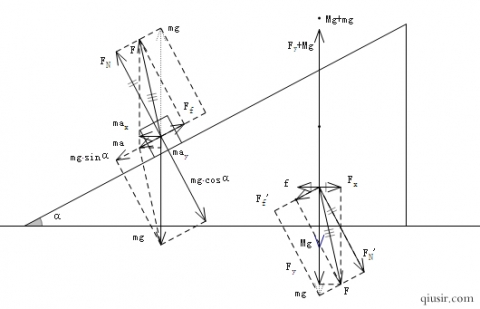
且无初速度释放,受力情况同上。如果摩擦系数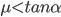 ,滑块会加速下滑,而其所受的弹力和摩擦力的合力在数值上小于重力,而方向上也不在竖直方向了...
静止在水平地面的斜面受到的滑块的压力和摩擦力的合力有水平方向的分量,所以必然受相反方向的静摩擦力。当然也可以从整体的考虑应用牛顿第二定律,
,滑块会加速下滑,而其所受的弹力和摩擦力的合力在数值上小于重力,而方向上也不在竖直方向了...
静止在水平地面的斜面受到的滑块的压力和摩擦力的合力有水平方向的分量,所以必然受相反方向的静摩擦力。当然也可以从整体的考虑应用牛顿第二定律,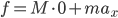 ,正是地面给斜面的水平摩擦力f提供系统的水平方向的加速度,而加速下滑的滑块使得系统质心有向下的加速度,处于失重状态,地面对斜面的支持力必然小于两个物体总重力。
对确定的接触面,摩擦系数为定值。而由
,正是地面给斜面的水平摩擦力f提供系统的水平方向的加速度,而加速下滑的滑块使得系统质心有向下的加速度,处于失重状态,地面对斜面的支持力必然小于两个物体总重力。
对确定的接触面,摩擦系数为定值。而由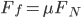 ,压力和摩擦力的夹角不变,当斜面的倾角也不变时,支持力和摩擦力的合力方向不随压力的变化而变化。
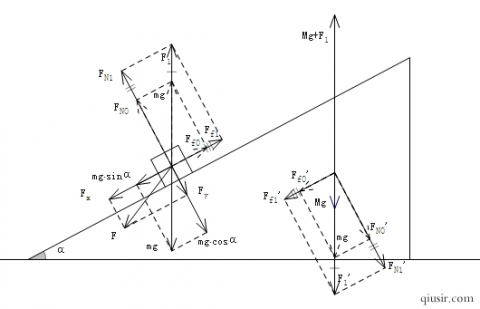
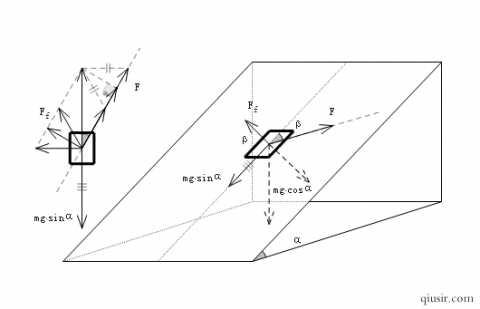
题如上图,如果滑块能独自够沿斜面匀速下滑,当对滑块施加斜向下的外力使其加速下滑时,斜面受到压力和摩擦力的反作用力合力仍然竖直向下,斜面没有水平运动趋势,一样不受地面的静摩擦力。
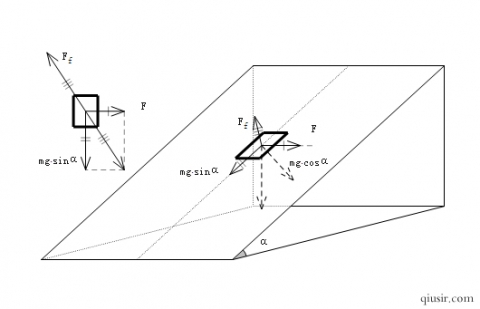
随着信息技术的发展,立体问题的探讨将是未来认知上的一个增长点。习惯了平面的媒介,也习惯了平面的思维,偶尔的空间问题,即便很简单也有认知的难度。
比如,水平外力F的作用下,斜面上的物体不会一如以前沿着斜面下滑,而是下滑力和外力的合力的反方向。如果滑块是匀速运动的话,会有如下方程:
,压力和摩擦力的夹角不变,当斜面的倾角也不变时,支持力和摩擦力的合力方向不随压力的变化而变化。
题如上图,如果滑块能独自够沿斜面匀速下滑,当对滑块施加斜向下的外力使其加速下滑时,斜面受到压力和摩擦力的反作用力合力仍然竖直向下,斜面没有水平运动趋势,一样不受地面的静摩擦力。
随着信息技术的发展,立体问题的探讨将是未来认知上的一个增长点。习惯了平面的媒介,也习惯了平面的思维,偶尔的空间问题,即便很简单也有认知的难度。
比如,水平外力F的作用下,斜面上的物体不会一如以前沿着斜面下滑,而是下滑力和外力的合力的反方向。如果滑块是匀速运动的话,会有如下方程:
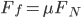
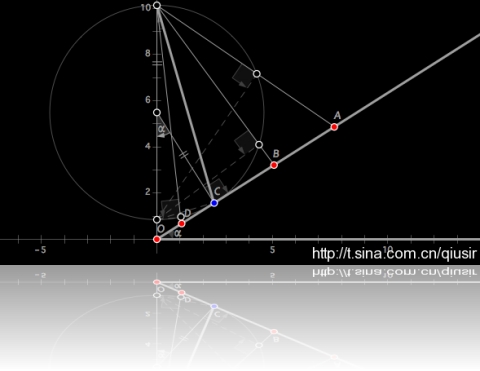
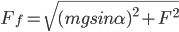 这是一道和前面相关的好题目,相关参数:静止在斜面上的滑块重力
这是一道和前面相关的好题目,相关参数:静止在斜面上的滑块重力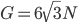 ,摩擦系数
,摩擦系数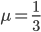 ,
,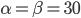 °,求F的大小。
°,求F的大小。
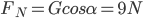 ,
,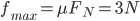 ,
,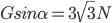 ...
这里的文字仅仅是提示用的,更多考虑可以参考图示。上一道题目答案
...
这里的文字仅仅是提示用的,更多考虑可以参考图示。上一道题目答案![F\in[3,6]](http://www.qiusir.com/wp-content/plugins/latex/cache/tex_eb97f89eb6b1ee6bac9720b5576bdeb8.gif) 。
GSP5文件下载:GSP-斜面放物图 (6829)
。
GSP5文件下载:GSP-斜面放物图 (6829)