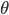AI助学麦克斯韦方程组

试着用gemini的学习辅导来学习
麦克斯韦(James Clerk Maxwell)是一位非常了不起的科学家,物理学家们常把他与牛顿和爱因斯坦并列。麦克斯韦最伟大的贡献把电和磁彻底“统一”在了一起。这组方程是以麦克斯韦命名的,但将它们提炼为现代教科书里那种简洁、对称的4个矢量方程形式的人,主要是英国物理学家、工程师亥维赛(Oliver Heaviside)
一、麦克斯韦方程组(积分形式)
1、高斯静电定律(有电荷的地方就有电场线“喷”出来或“吸”进去。)

2、高斯磁定律(磁场线总是闭合的,没有起点也没有终点。这也意味着世界上不存在磁单极子。)

3、法拉第电磁感应定律(那个负号代表产生的电场总是试图阻止磁场的变化。)

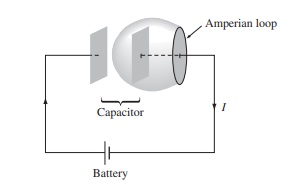
4、安培-麦克斯韦定律(磁场可以由两种方式产生:一是电流I,二是变化的电场。这是麦克斯韦最伟大的补充,正是这一项预言了电磁波的存在。)

这四个方程就像是一场双人舞:变化的磁场产生电场,变化的电场又产生磁场。它们互为因果,循环往复。
二、麦克斯韦方程组的微分形式,两个核心概念:散度(Divergence)和旋度(Curl)。它们不再描述整个区域,而是描述空间中每一个点上的电磁场是如何变化的。我们可以把这四个方程看作是电磁场的“局部基因图谱”:
1、电场的散度(高斯定律)(描述电荷如何产生电场)

 (读作del dot)散度衡量的是向量场从一个点“发散”出来的程度。
(读作del dot)散度衡量的是向量场从一个点“发散”出来的程度。
电荷密度ρ是电场的源头。正电荷就像喷泉(散度为正),负电荷就像漏斗(散度为负)。
2、磁场的散度(高斯磁定律)(描述磁单极子不存在)

磁场的散度永远为0,这意味着磁场没有起点也没有终点,磁场线总是闭合的。
散度(Divergence):想象水管里的水。如果一个地方有喷头在喷水,那里的散度就是正的,这一点就像是一个“源头”(Source);如果有排水口,散度就是负的,这一点就是一个“汇”(Sink)。
 ,向量场F偏导数的运算。
,向量场F偏导数的运算。
一个向量场通过闭合曲面的通量等于该曲面所包围体积内的散度的体积积分。
3、电场的旋度(法拉第定律)(描述变化的磁场如何产生旋转的电场)

 (读作 del cross)是旋度,它衡量的是向量场在一个点附近“打转”的程度。
(读作 del cross)是旋度,它衡量的是向量场在一个点附近“打转”的程度。
变化的磁场(磁场对时间的导数)会在周围感生出一个旋转的电场。
4、磁场的旋度(安培-麦克斯韦定律)(描述电流和变化的电场如何产生旋转的磁场)

磁场的“旋涡”有两个来源:一是电流密度,二是变化的电场。
旋度(Curl):想象水面上有一个小木片。如果水流让小木片原地转圈,说明那里的水流旋度不为 0。

旋度和斯托克斯定理(Stokes' Theorem)密切相关,后者表示曲线围成的闭合环路上某向量场的线积分等于该曲面上的旋度的曲面积分

我们已经讨论了散度(源头)和旋度(旋转),你觉得如果一个向量场的散度和旋度在空间中每一处都被确定了,这个场是不是就被唯一确定了呢?(这涉及到一个著名的物理定理——亥姆霍兹定理)。
三、张量形式

张量形式的麦克斯韦方程组是更为一般的表达方式,通常用于相对论框架下。
洛伦兹力方程:
虽然不完全是麦克斯韦方程的一部分,但洛伦兹力方程描述了电磁场对带电粒子的作用。
四、范例
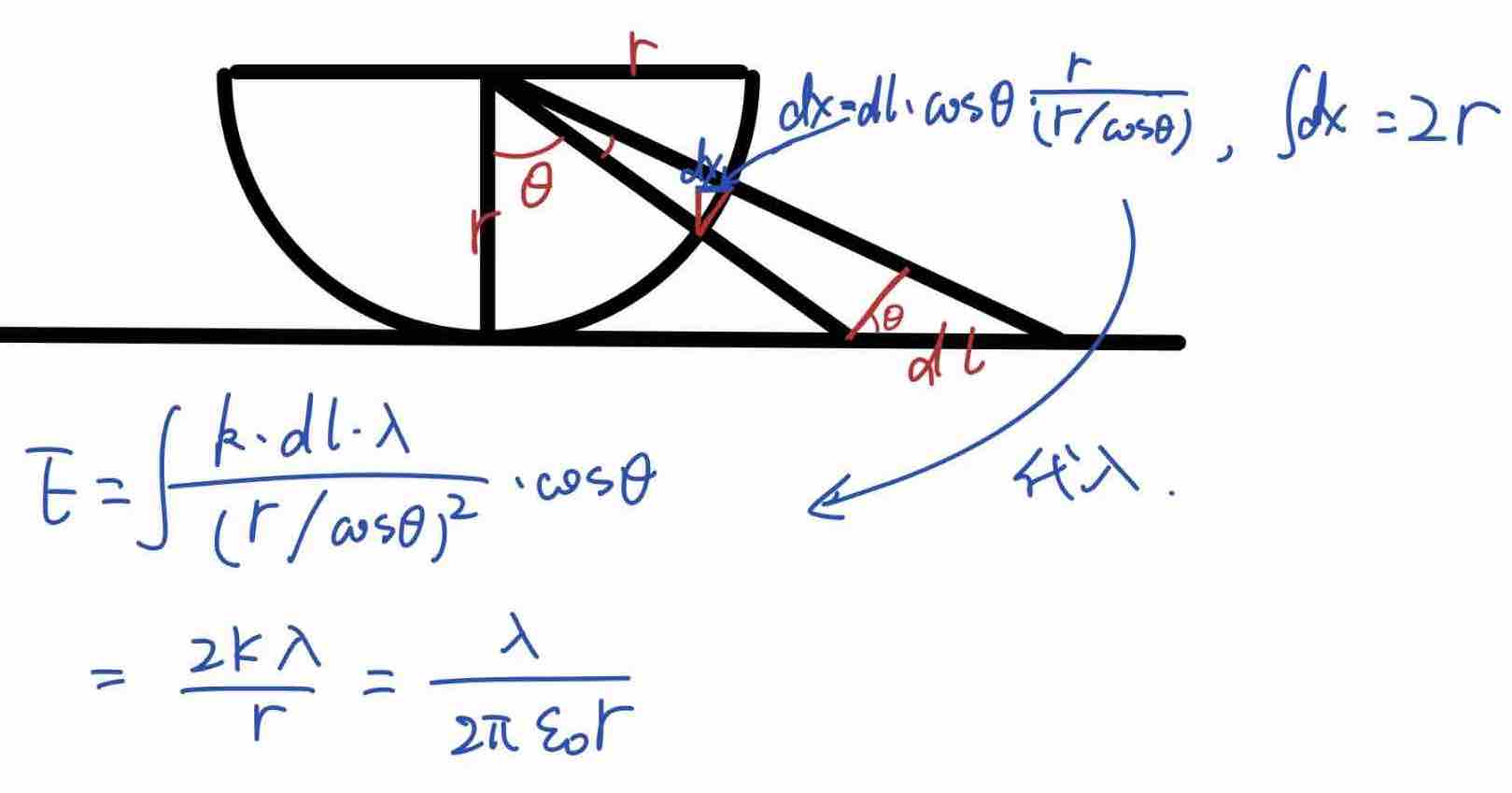
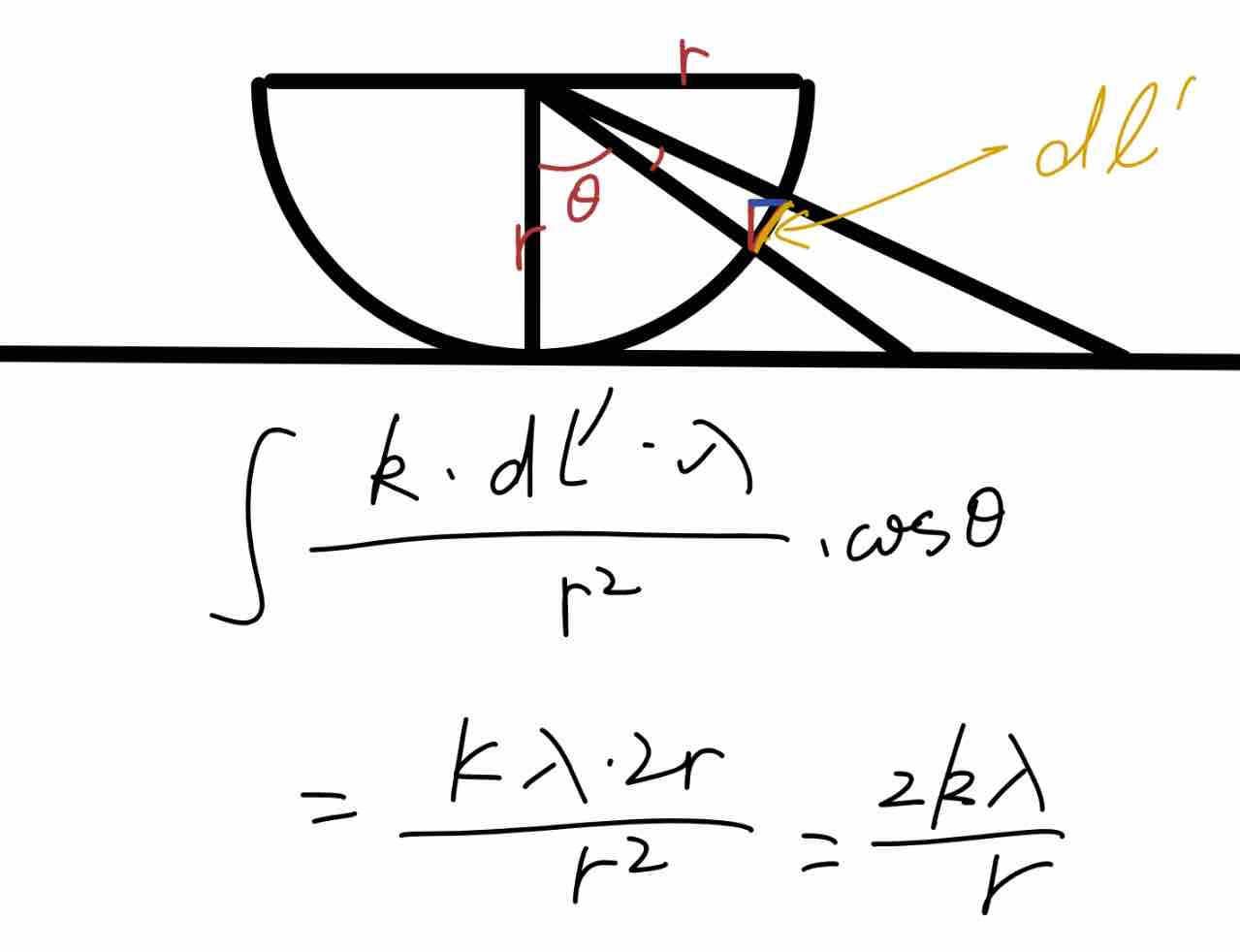
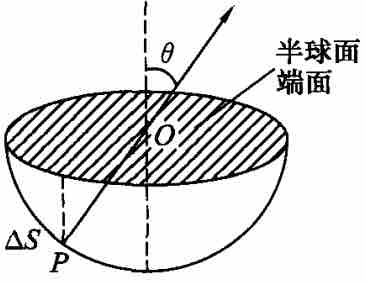
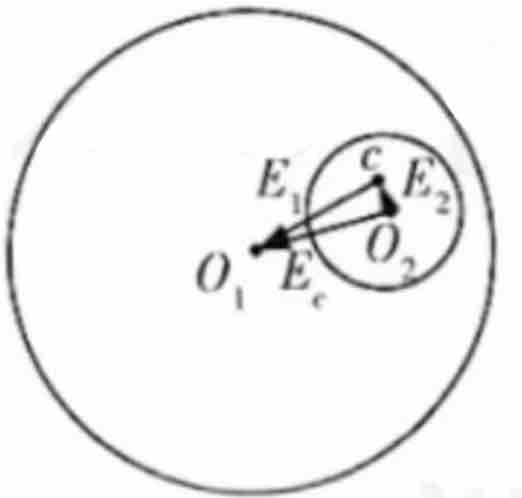
1、均匀带电球体、球壳、无限长带电导线和无限大带电平面的电场,利用对称性,选取高斯面,球面、圆柱面、药丸盒
ChatGPT对于环形电流中心处磁场,竟用“安培定理”(安培环形定理)给出一堆的顾左右而言它的解释,让它出图示,竟然也给出看着很正确的东西,当然,当你发现问题后,它会告诉你用比奥-萨伐尔定律···
很正确的样子
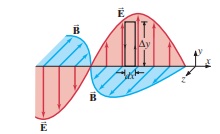
2、推导光速
在没有任何电荷和电流的真空中,麦克斯韦方程组表现出高度的对称性:




对法拉第定律取旋度

使用矢量恒等式展开左边

代入真空条件和安培-麦克斯韦定律

得到电场波动方程

类比经典物理中波动方程通式
结合推导结果得出光速
五、注释
1. (Del/Nabla)是一个算子,通常被称为Nabla算子,是一组操作指令。像一个“多功能工具刀”,在三维空间中指向函数变化最快的方向。用于计算梯度(Gradient)、散度(Divergence)和旋度(Curl)。
(Del/Nabla)是一个算子,通常被称为Nabla算子,是一组操作指令。像一个“多功能工具刀”,在三维空间中指向函数变化最快的方向。用于计算梯度(Gradient)、散度(Divergence)和旋度(Curl)。
2. (Delta)是一个预定义的变化量,通常代表“差值”。
(Delta)是一个预定义的变化量,通常代表“差值”。
在微积分中,它也代表拉普拉斯算子, ,用来衡量一个场在某一点与其周围平均值的差异。
,用来衡量一个场在某一点与其周围平均值的差异。

AI画图,让我想起求师得最初的slogan,a Question a Chance!不是不是应该改成A Question An Apple






![D(x,t) = A \sin \left[ \frac{2\pi}{\lambda} (x - vt) \right]](http://www.qiusir.com/wp-content/plugins/latex/cache/tex_83853f7dc9aad0392bdb04ba0532e292.gif)

































![k E_0 \cos(\dots) = - [-\omega B_0 \cos(\dots)]](http://www.qiusir.com/wp-content/plugins/latex/cache/tex_2641e3e0fe68ac7723c5b54d73fd904c.gif)


![- k B_0 \cos(\dots) = \mu_0 \epsilon_0 [-\omega E_0 \cos(\dots)]](http://www.qiusir.com/wp-content/plugins/latex/cache/tex_c11408563e7647597ad5026444fe0e59.gif)