从费马原理到最速降线

十 27

从费马原理到最速降线

研教|〖席明纳理〗肖遥 2025

JQX/进取芯席明纳第15期（2025.10.16）

从费马原理到最速降线

JQX|Xiao

1.伯努利与最速降线
在 17 世纪，约翰·伯努利（Johann Bernoulli）在思考最速降线问题时，受到了光学中“费马最短时间原理”的启发。费马指出：光线在传播时，总是选择一条能使它从出发点到达目标点所需时间最短的路径。
通过这一原理可推导出斯涅尔定律。当光从一种介质进入另一种介质时，传播速度发生变化，光线发生折射，而其入射角和折射角满足： $\frac{\sin\theta_1}{v_1} = \frac{\sin\theta_2}{v_2} = \text{C}$
其中 $v_1,v_2$ 分别是光在两种介质中的速度。伯努利的关键思想是把物体下滑的路径与光的传播类比。伯努利设想：把空间分成由折射率不同的介质组成的一层层的结构。若把粒子在重力场中下滑的路径比作光线在不同介质中的传播，那么下滑路径的不同高度就好比不同折射率的层。物体下落的速度 $v$ 取决于高度 $y$ ，由能量守恒有 $v \propto \sqrt{y}$ ，由于光总是沿着时间最短的路径传播，所以如果粒子的运动路径与光相同，那么它的轨迹就是最速降线。根据斯涅尔定律： $\frac{v}{\sin\theta} = \text{C}$ ，带入机械能守恒方程，于是得到最速降线的微分关系： $\frac{\sin\theta}{\sqrt{y}} = k$ 。

2.摆线方程证明

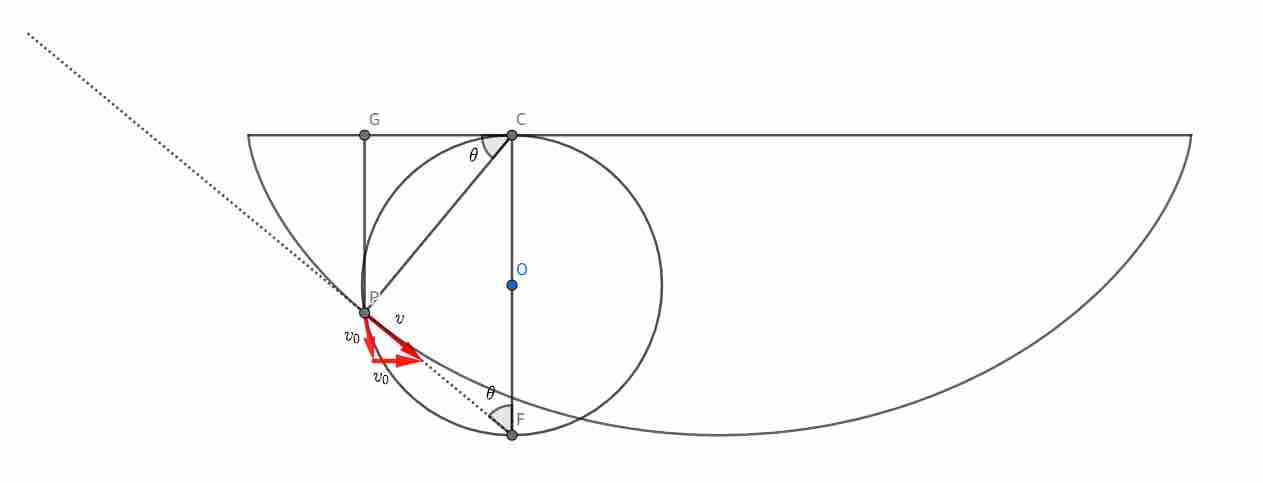
按照伯努利的说法，他一眼就看出这是摆线的方程。下面引用马克·莱维的方法对这个公式进行证明。设想一个在天花板上滚动的轮子，轮缘上的一点 P 描绘出一条倒置的摆线。轮与天花板的接触点 C 是这一瞬间的瞬时旋转中心。此时，点 P 的运动相当于以 C 为支点的圆周运动。圆的切线与半径垂直，摆线在 P 点的切线垂直于 PC。 PC 与圆的直径构成直角三角形，斜边是圆的直径。通过相似三角形关系，可以得到： $y = (\text{D}) \cdot \sin^2\theta$ 于是立刻有： $\frac{\sin\theta}{\sqrt{y}} = \frac{1}{\sqrt{\text{D}}} = \text{C}$ 这正是伯努利得到最速降线方程的关键条件。因此，摆线满足 $\sin\theta/\sqrt{y}$ 为常数的性质。几何与物理在此奇妙地契合——摆线的几何构造，正体现了自然界中“时间最短”的运动规律。

3. 最速降线圆心速度分析
摆线是由于轮子滚动时轮子上的一点形成的，那么当轮子如何滚动时，滚出的摆线轨迹与小球沿最速降线下滑时刚好吻合，或者说小球沿最速降线下滑时，对应的圆的圆心速度大小是多少？
物体在摆线上的运动可以看成由两部分组成，分别是是圆心的平动速度和相对于圆心的转动速度。如图中所示，其中平动速度水平向右，转动速度沿圆周运动的切线方向。由几何关系可知： $2v_0\sin\theta = \sqrt{2gy}.$ 根据摆线方程： $y = D \sin^2\theta = 2R \sin^2\theta$ .以及机械能守恒： $v = \sqrt{2gy}$ .可以得到 $v_0 = \sqrt{gR}$ ，其中 $v_0$ 与g、R均为常数。这说明最快下落的路径对应轮子上一点匀速转动过的轨迹。