摆线的等时性与变分法

十一 10

摆线的等时性与变分法

研教|〖席明纳理〗肖遥 2025

JQX/进取芯席明纳第18期（2025.10.30）

摆线的等时性与变分法

JQX|Jin
一：摆线的等时性
摆线在弧长方向满足简谐振动，因此与弹簧振子相同，震动周期与振幅无关，因此满足等时性。下面从能量的角度证明沿摆线下落的物体满足简谐振动。摆线方程为：

$x=R(\theta-\sin\theta),\qquad y=R(1-\cos\theta)$ ,把最低点作为势能零点：最低点对应

$\theta=\pi$ 。
记从最低点到轨道上一点P的弧长为

$s\ge 0$ ，向上为正；P的高度为

$h\ge 0$ 。
1) 弧长微分

$x'(\theta)=\frac{dx}{d\theta}=R(1-\cos\theta),\; y'(\theta)=\frac{dy}{d\theta}=R\sin\theta,\; ds=\sqrt{(dx)^2+(dy)^2}=\sqrt{(x')^2+(y')^2}\,d\theta=2R\sin\frac{\theta}{2}\,d\theta.$
因此从

$\theta=\pi$ 到任意

$\theta$ 的弧长为

$s(\theta)=\int_{\pi}^{\theta}2R\sin\frac{\varphi}{2}\,d\varphi=4R\cos\frac{\theta}{2}.$
2) 从最低点计的高度

$h(\theta)=y(\theta)-y(\pi)=R(1-\cos\theta)-2R=2R\cos^2\frac{\theta}{2}.$
3)

$h$ 与

$s$ 的关系
由

$s=4R\cos\frac{\theta}{2}$ 得

$\cos\frac{\theta}{2}=\frac{s}{4R}$ ，代入上式：

$h=\frac{s^{2}}{8R}.$
4) 能量方程
设质点质量为 m，切向速度

$v=\dot s$ 。能量守恒：

$E=\frac12 m v^2 + m g h =\frac12 m \dot s^{\,2} + m g\frac{s^2}{8R} =\frac12 m \dot s^{\,2}+\frac12\,k' s^2,$ 。其中

$k'=\frac{m g}{4R}$
这恰是一维简谐振动的能量形式，角频率

$\omega=\sqrt{\frac{k'}{m}}=\sqrt{\frac{g}{4R}}.$ 。利用简谐振动周期公式

$T=\frac{2\pi}{\omega}=4\pi\sqrt{\frac{R}{g}},\qquad t=\frac{T}{4}=\pi\sqrt{\frac{R}{g}}.$
周期与起点高度无关，所以摆线满足等时性。
二：变分法
牛顿只用了一晚就解决了约翰·伯努利对于最速降线的挑战的故事一直为人津津乐道，当时共有五个人给出了最速降线的解决办法。除了约翰·伯努利的巧妙办法外，他的哥哥雅各布·伯努利更是开启了变分法的开端，几十年后欧拉和拉格朗日把这个方法系统化为变分法，并提出欧拉-拉格朗日方程。下面用E-L方程来证明最速降线为摆线。
1、时间泛函
最速降线问题为一个小球在重力作用下从高处滑向低处，其运动轨迹曲线为

$y = y(x)$ 。根据能量守恒定律，小球在任意位置的速度为

$v = \sqrt{2gy}$ 。设微元弧长为

$dl = \sqrt{dx^2 + dy^2} = \sqrt{1 + y'^2}\,dx$ ，则走过这段微小弧长所用的时间元为

$dt = \frac{dl}{v} = \frac{\sqrt{1 + y'^2}}{\sqrt{2gy}}\, dx$ 。因此，小球滑完全程的总时间可以表示为一个积分泛函

$T = \int_{x_1}^{x_2} \frac{\sqrt{1 + y'^2}}{\sqrt{2gy}}\, dx$ ，我们要求解的就是能使 T 最小的曲线

$y(x)$ 。
2、求解E-L方程
为了求出极值曲线

$y(x)$ ，我们引入一个在边界点为零的微小扰动函数

$\eta(x)$ ，并构造一条扰动后的曲线

$\bar{y}(x) = y(x) + \varepsilon \eta(x)$ 。其中

$\varepsilon$ 为微小常数，且边界条件满足

$\eta(x_1) = \eta(x_2) = 0$ ，以保证扰动不改变曲线的端点位置。
原时间泛函可以写为

$T[y] = \int_{x_1}^{x_2} F(x, y, y')\, dx$ ，其中被积函数为

$F(x, y, y') = \frac{\sqrt{1 + y'^2}}{\sqrt{2gy}}$ 。将扰动后的曲线

$\bar{y} = y + \varepsilon \eta$ 及其导数

$\bar{y}' = y' + \varepsilon \eta'$ 代入，泛函就变成了关于

$\varepsilon$ 的函数

$T(\varepsilon) = \int_{x_1}^{x_2} F(x, y + \varepsilon\eta, y' + \varepsilon\eta')\, dx$ 。
为了求得泛函的极值，我们需要其对

$\varepsilon$ 的一阶变分为零，即

$\frac{dT}{d\varepsilon}\Big|_{\varepsilon=0} = 0$ 。首先计算导数：

$\frac{dT}{d\varepsilon} = \int_{x_1}^{x_2} \left( \frac{\partial F}{\partial y}\eta + \frac{\partial F}{\partial y'}\eta' \right) dx$ 。当

$\varepsilon = 0$ 时，此式依然成立。
我们对积分的第二项使用分部积分法（

$\int u\,dv=uv-\int v\,du$ ）。令

$u=\frac{\partial F}{\partial y'}$ 且

$dv=\eta'\,dx$ ，则可得到

$v=\eta$ 和

$du=\frac{d}{dx}\!\left(\frac{\partial F}{\partial y'}\right)dx$ 。于是，积分项变为

$\int_{x_1}^{x_2}\frac{\partial F}{\partial y'}\,\eta'\,dx =\left[\frac{\partial F}{\partial y'}\,\eta\right]_{x_1}^{x_2} -\int_{x_1}^{x_2}\eta\,\frac{d}{dx}\!\left(\frac{\partial F}{\partial y'}\right)dx$ 。
由于边界处的扰动为零，即

$\eta(x_1)=\eta(x_2)=0$ ，所以

$\left[\frac{\partial F}{\partial y'}\,\eta\right]_{x_1}^{x_2}$ 这一项为零。最终我们得到

$\frac{dT}{d\varepsilon}\Big|_{\varepsilon=0} = \int_{x_1}^{x_2}\!\left( \frac{\partial F}{\partial y} -\frac{d}{dx}\!\left(\frac{\partial F}{\partial y'}\right) \right)\eta\,dx=0$ 。
根据变分法基本引理，因为

$\eta(x)$ 是任意的微小扰动，要使上式恒成立，必须其括号内的部分为零。这样，我们就得到了著名的欧拉-拉格朗日方程：

$\frac{\partial F}{\partial y} -\frac{d}{dx}\!\left(\frac{\partial F}{\partial y'}\right)=0$ 。
3、Beltrami恒等式及其应用
在某些特殊情况下，欧拉-拉格朗斯方程可以被简化。一个重要的情形是当被积函数

$F(x, y, y')$ 不显式地依赖于

$x$ 时（即

$\frac{\partial F}{\partial x} = 0$ ），存在一个被称为**贝尔特拉米恒等式 (Beltrami Identity)** 的一阶积分：

$F - y' \frac{\partial F}{\partial y'} = C$ ，其中 C 是一个常数。这个恒等式可以大大简化求解过程。
现在，我们把这个强大的工具应用到最速降线问题上。回顾我们的时间泛函被积函数

$L = \frac{\sqrt{1 + y'^2}}{\sqrt{2gy}}$ ，它显然不显式地含有变量

$x$ ，因此完全满足使用贝尔特拉米恒等式的条件。
我们首先计算

$L$ 对

$y'$ 的偏导数：

$\frac{\partial L}{\partial y'} =\frac{1}{\sqrt{2g}}\frac{y'}{\sqrt{y}\sqrt{1+y'^2}}$ 。然后将

$L$ 和

$\frac{\partial L}{\partial y'}$ 代入恒等式

$L-y'\,\frac{\partial L}{\partial y'}=C$ 。经过化简，我们得到一个非常简洁的关系式：

$\frac{1}{\sqrt{2g}}\frac{1}{\sqrt{y}\sqrt{1+y'^2}}=C$ 。
4、求解方程，证明曲线为摆线
为了求解上面这个关于

$y$ 和

$y'$ 的微分方程，我们首先将所有常数合并为一个新的常数

$k$ ，得到

$\frac{1}{\sqrt{y}\sqrt{1+y'^2}}=k$ 。整理后可解出

$y'$ 的表达式：

$y'^2=\frac{1-k^2y}{k^2y}$ 。
为了对该方程积分，我们采用一个技巧，求解

$x$ 关于

$y$ 的导数

$\frac{dx}{dy}=\frac{1}{y'}=\sqrt{\frac{k^2 y}{1-k^2 y}}$ 。这个形式的积分可以通过参数代换来解决。我们引入参数

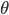$\theta$ ，并令

$y=\frac{1}{k^2}\sin^2\!\frac{\theta}{2}$ ，它等价于

$y=\frac{1-\cos\theta}{2k^2}$ 。
进行代换后，表达式被简化为：

$\frac{dx}{dy}=\sqrt{\frac{(1-\cos\theta)/2}{(1+\cos\theta)/2}} =\tan\frac{\theta}{2}$ 。同时，我们可以求出

$dy=\frac{1}{2k^2}\sin\theta\,d\theta$ ，因此

$dx=\tan\frac{\theta}{2}\,dy = \frac{1}{k^2}\sin^2\!\frac{\theta}{2}\,d\theta$ 。对

$dx$ 积分可得

$x=\frac{1}{2k^2}\int (1-\cos\theta)\,d\theta =\frac{1}{2k^2}\bigl(\theta-\sin\theta\bigr)+C_x$ ，其中

$C_x$ 是积分常数。
最后，我们整理一下结果。令常数半径

$R=\frac{1}{2k^2}$ ，并将积分常数合并为起点坐标

$(x_0, y_0)$ ，我们便得到了该曲线的最终参数方程：

$\begin{aligned} x(\theta) &= R\bigl(\theta-\sin\theta\bigr) \\ y(\theta) &= R\bigl(1-\cos\theta\bigr) \end{aligned}$
这正是摆线（Cycloid）的标准参数方程。至此，我们证明了最速降线确实是一条摆线。

下期预告：邀请上一期提供巧思的K2304班吴尚达同学，带来一些做功问题的新思考

On this day..

Comments are closed.