一些做功与能量问题新观点
JQX/进取芯 席明纳第19期(2025.11.06)

一些做功与能量问题新观点

浑南高中部K2304班 吴尚达
能量是高中物理的核心物理量之一,其转化通过力的做功实现,力做功也必然涉及能量之间的互相转化。
一、机械能,保守力与非保守力
机械能是指物体由于其运动和位置而具有的能量,它是一个由相互作用的物体组成的系统的动能和势能的总和,即  。
。
保守力指做功与路径无关的力,如重力、引力等,保守力的做功只与其位移有关,那么只要知道保守力关于位移的函数,我们就能通过积分得到它对于一段位置变化做的功,进而得到它的势能函数。对于常见的一次函数形式的保守力,积分势能的过程如下: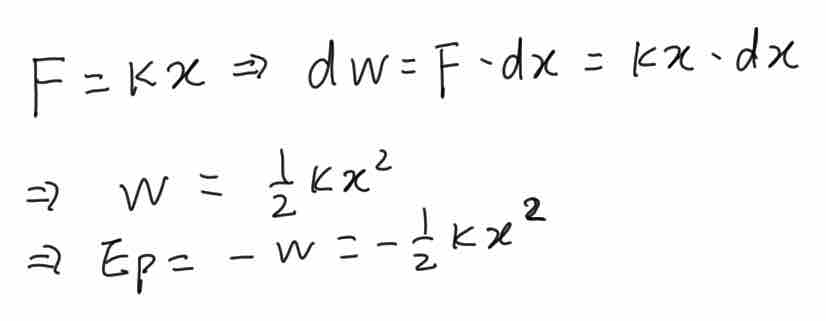
qiusir说:“保守力的英文是conservative force,与‘守恒’同源,故也称守恒力,在日本教材中也称‘保存力’,这种力的作用效果是保存能量,使其仅在系统内部发生转化,动能和势能通过做功重新分配而不与外界发生能量的流动”也就是说,能量在一个孤立封闭系统内部转化,我们把这种系统称为保守系统。
非保守力与保守力的定义相反,如果做功的力是非保守力,比如摩擦力,那么它会把系统的能量耗散出去,这就是一个开放系统。
让我们看一道个人很喜欢的例题:
【例零】如图所示,一盛水容器绕竖直中心轴以角速度 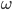 匀速转动,求水面的函数。
匀速转动,求水面的函数。
我们以旋转的桶为参考系,那么液面就是静止的,由于参考系是非惯性参考系,我们需要引入惯性离心力,同时引入离心势能的概念,这样水面上一定质量的液体,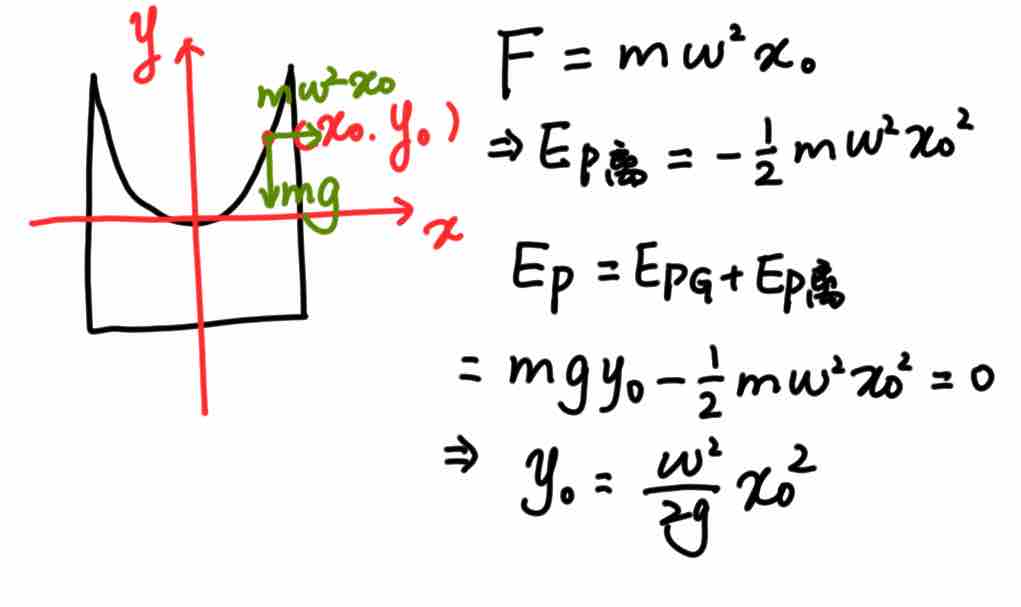 它的势能为重力势能与离心势能的总和。对于一个液面,它一定是一个等势面(如果同一液面上存在较高势能的点和较低势能的点,那么较高势能点处的液滴就会向较低势能方向运动,最终形成一个等势面),对于这个等势面,我们可以定义它的势能为任意常数,这里定义为零,对其能量列式如下:
它的势能为重力势能与离心势能的总和。对于一个液面,它一定是一个等势面(如果同一液面上存在较高势能的点和较低势能的点,那么较高势能点处的液滴就会向较低势能方向运动,最终形成一个等势面),对于这个等势面,我们可以定义它的势能为任意常数,这里定义为零,对其能量列式如下:
(如果定义水面的势能为常数  ,则对应的函数应多一项
,则对应的函数应多一项  ,液面形状依旧是抛物线)
,液面形状依旧是抛物线)
qiusir还提出了受力分析的解法:
二、力的“作用质点”的位移
【例一】光滑水平地面上用恒力  拉动静止的物体
拉动静止的物体  , 夹角为
, 夹角为 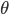 ,物体前进位移
,物体前进位移  , 求这段过程中恒力
, 求这段过程中恒力  所做的功
所做的功 
对于这道题,qiusir给出了比较标准的叙述方法: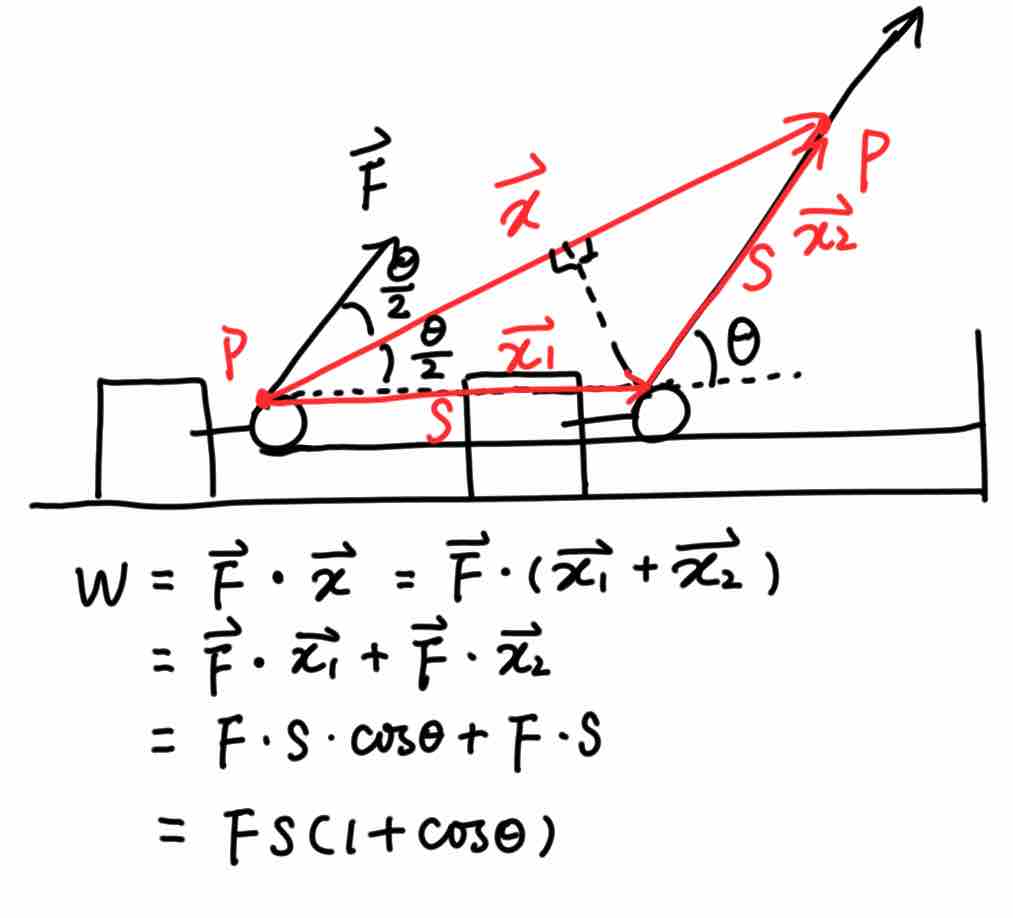
这道典型例题中,可以认为力是一直作用在同一个作用点  上的,但如果力的作用点是时刻变化的呢?
上的,但如果力的作用点是时刻变化的呢?
【例二】如图为打印机滚轮辅助进纸装置,轮子半径为  ,绕过
,绕过  点的固定轴以角速度
点的固定轴以角速度 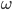 匀速转动, 带动下方纸张以速度
匀速转动, 带动下方纸张以速度  运动, 试求转动一周摩擦力
运动, 试求转动一周摩擦力  所做的功。
所做的功。
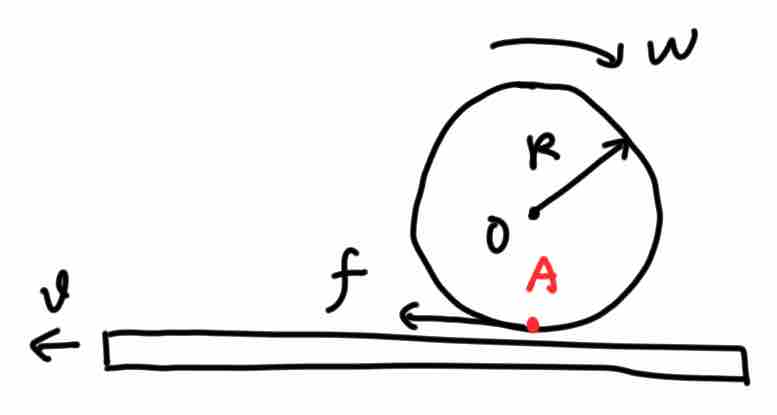
经过一定时间图中 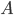 点将不再与白纸接触,摩擦力的作用点不再是
点将不再与白纸接触,摩擦力的作用点不再是 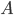 点,那么是否可以认为摩擦力的作用点的位移为零呢?因为纸获得的动能,所以显然
点,那么是否可以认为摩擦力的作用点的位移为零呢?因为纸获得的动能,所以显然  做的功不为零。
做的功不为零。
通过“作用质点”来解释这一现象:
对于任意系统,当我们将其离散化,都可以得到无数个无穷小的质点(质量元),作用质点是指某一时刻力作用的系统的一质量元。 力的做功其实是由很多个微小的做功过程组成的,当力的作用质点可认定不变时,它就是我们所说的作用点,从而通过其位移计算出做功,但当力的直接作用点发生变化时,则需要通过积分转化来求做功。
力的做功其实是由很多个微小的做功过程组成的,当力的作用质点可认定不变时,它就是我们所说的作用点,从而通过其位移计算出做功,但当力的直接作用点发生变化时,则需要通过积分转化来求做功。
三、惯性系与非惯性系的影响
动能定理,机械能守恒是在牛顿第二定律成立的基础上推导出来的。牛顿第二定律在任意惯性系中仍然成立,所以以其为基础的能量动量方面的定理自然也是成立的。
故:在地面系下,如果动量守恒,则在另一惯性系下,动量仍是守恒的;在地面系下,如果机械能是守恒的,则在另一惯性系下,机械能照样是守恒的。
当然也可以通过一些矢量推导(以下推导中  、
、 均为矢量)证明出来:
均为矢量)证明出来:
A,B,C三个可视为质点物体(可拓展至  个)与地球构成一个系统,三个物体分别受外力
个)与地球构成一个系统,三个物体分别受外力  ,
, ,
, 的作用,在一个与地面保持静止的参考系
的作用,在一个与地面保持静止的参考系  中观测到此系统在运动过程中动量守恒,机械能也守恒,
中观测到此系统在运动过程中动量守恒,机械能也守恒, 是相对于
是相对于  做匀速直线运动的参考系
做匀速直线运动的参考系
由  系中动量守恒可知合外力
系中动量守恒可知合外力  为零由于受力与参考系无关,所以在
为零由于受力与参考系无关,所以在  系下合外力
系下合外力  依旧为零,合力对系统做总冲量为0,动量守恒得证。
依旧为零,合力对系统做总冲量为0,动量守恒得证。
设很短时间  内 ABC 三个物体的位移分别为
内 ABC 三个物体的位移分别为 

 ,
, 系中机械能守恒,故可知合外力总功为零,即
系中机械能守恒,故可知合外力总功为零,即

设同一时间间隔  内
内  系相对
系相对  系的位移为
系的位移为  则由相对运动知识可知:
则由相对运动知识可知:
A在  系下的位移
系下的位移 
A在  系下的位移
系下的位移 
B,C同理
故在  系中三个力做功之和为
系中三个力做功之和为



 系中机械能守恒得证。
系中机械能守恒得证。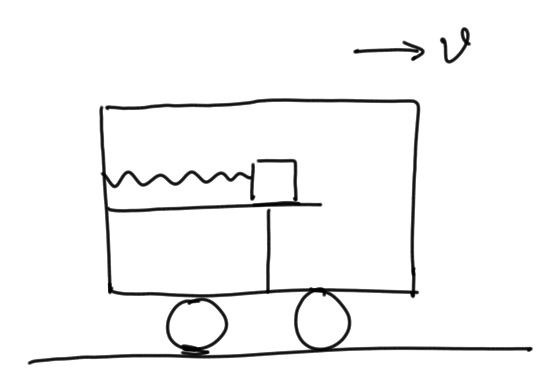
【例三】如图所示,火车以速度  向前做匀速运动,内有一光滑桌面,上有一轻质弹簧,右端有一质量为
向前做匀速运动,内有一光滑桌面,上有一轻质弹簧,右端有一质量为  的物体(不连接弹簧),一端固定于车厢壁,用手压缩一段后放手,物体被弹开(仍在桌面上),离开弹簧时相对车厢的速度为
的物体(不连接弹簧),一端固定于车厢壁,用手压缩一段后放手,物体被弹开(仍在桌面上),离开弹簧时相对车厢的速度为  。问:从放手到物体离开弹簧的瞬间,车厢壁对弹簧做了多少功?
。问:从放手到物体离开弹簧的瞬间,车厢壁对弹簧做了多少功?
应用上述知识,给出解答如下:
如果以非惯性系作为参考系,由于非惯性系中牛顿第二定律不再成立,需要引入惯性力,若引入的惯性力是保守力,则该系统依旧为保守系统,引入惯性力对应的势能后能量守恒
【例四】如图所示,一光滑细杆绕竖直轴以匀角速度转动,细杆与竖直轴夹角 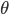 保持不变,一个相对细杆静止的小环自离地面
保持不变,一个相对细杆静止的小环自离地面  高处沿细杆下滑,求小环滑到细杆下端时的速度
高处沿细杆下滑,求小环滑到细杆下端时的速度 
以细杆为参考系引入惯性离心力  (科里奥利力方向与圆环运动方向垂直不做功,这里忽略不计),由保守系统能量守恒列式如下:
(科里奥利力方向与圆环运动方向垂直不做功,这里忽略不计),由保守系统能量守恒列式如下:

四、虚功原理
对于一个平衡系统,可以假设其发生了一个极为微小的变化,某个力做了一个微小的功  使系统的势能发生了一个微小的变化
使系统的势能发生了一个微小的变化  然后由
然后由  求出我们所需要的量,一般常用于求解一些力的大小。
求出我们所需要的量,一般常用于求解一些力的大小。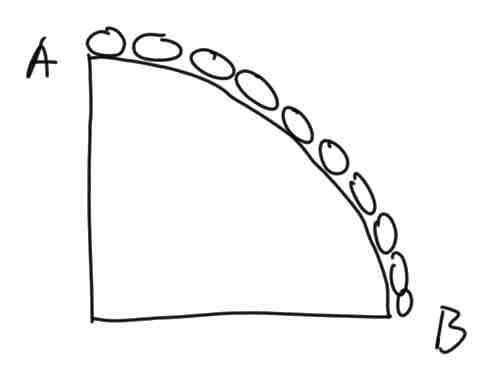
【例五】如图所示,一个半径为  的
的  光滑球面固定在水平桌面上,球面上放置一光滑均匀铁链,其
光滑球面固定在水平桌面上,球面上放置一光滑均匀铁链,其 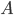 端受到一水平向左的拉力
端受到一水平向左的拉力  ,
,  端恰与桌面不接触,铁链单位长度的质量为
端恰与桌面不接触,铁链单位长度的质量为  ,求
,求  的大小
的大小
对铁链应用虚功原理,假设铁链在 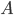 点拉力的作用下水平向左发生微小位移
点拉力的作用下水平向左发生微小位移  ,则拉力所做的功等于将
,则拉力所做的功等于将  点对应质量
点对应质量  抬升到了
抬升到了 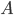 点,所以
点,所以
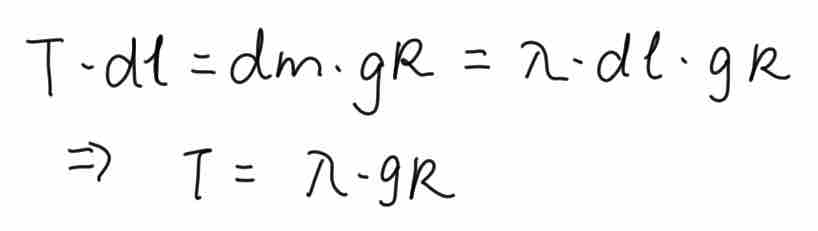
当然,本题也可以使用微元法求解:
qiusir:“类似的题目也曾在高一的某次考试中出现。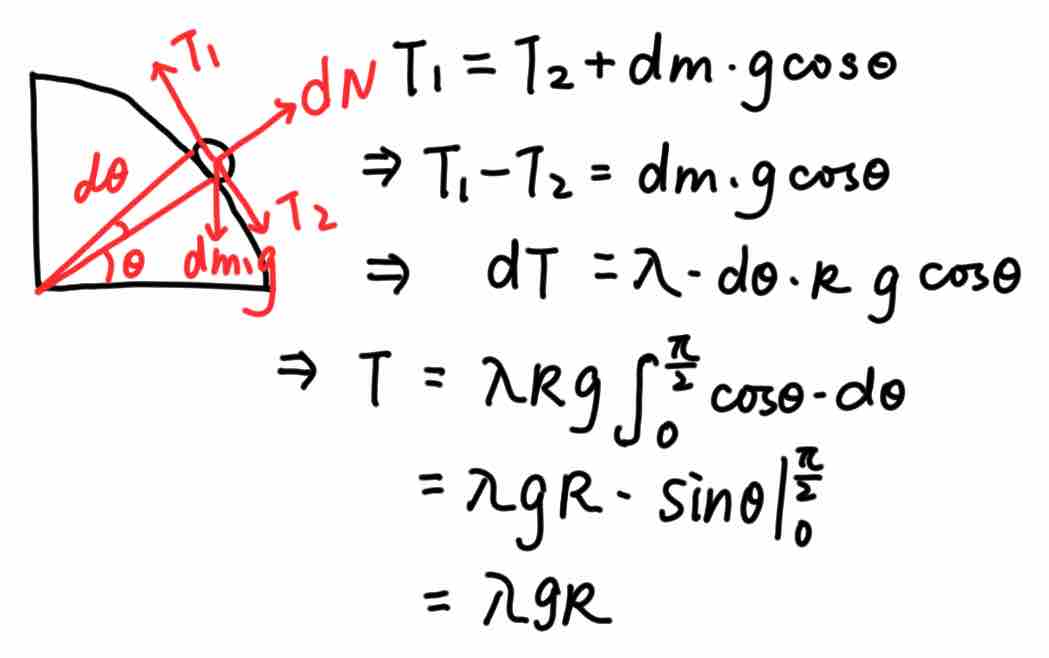 用几何分析的方法十分复杂繁琐,如果能巧妙的运用虚功原理,将大大节省做题时间”
用几何分析的方法十分复杂繁琐,如果能巧妙的运用虚功原理,将大大节省做题时间”
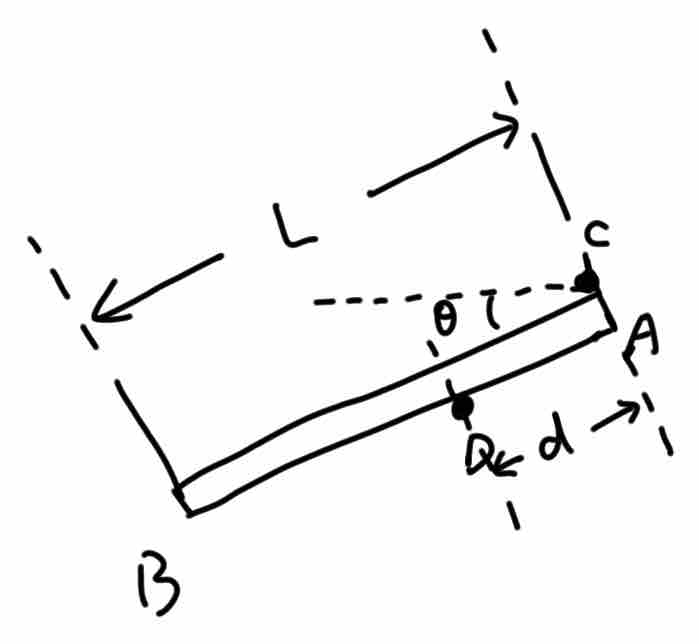 【例六】如图,一长为
【例六】如图,一长为  的匀质细杆
的匀质细杆  由固定的两个水平细轴
由固定的两个水平细轴  、
、 支撑在竖直平面内,
支撑在竖直平面内, 间距为
间距为  ,
, ,杆的
,杆的 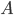 端置于轴
端置于轴  下, 杆与轴之间静摩擦系数为
下, 杆与轴之间静摩擦系数为  , 杆与水平面夹角为
, 杆与水平面夹角为 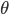 ,为使杆保持平衡,
,为使杆保持平衡,  比
比  的值必须满足什么条件
的值必须满足什么条件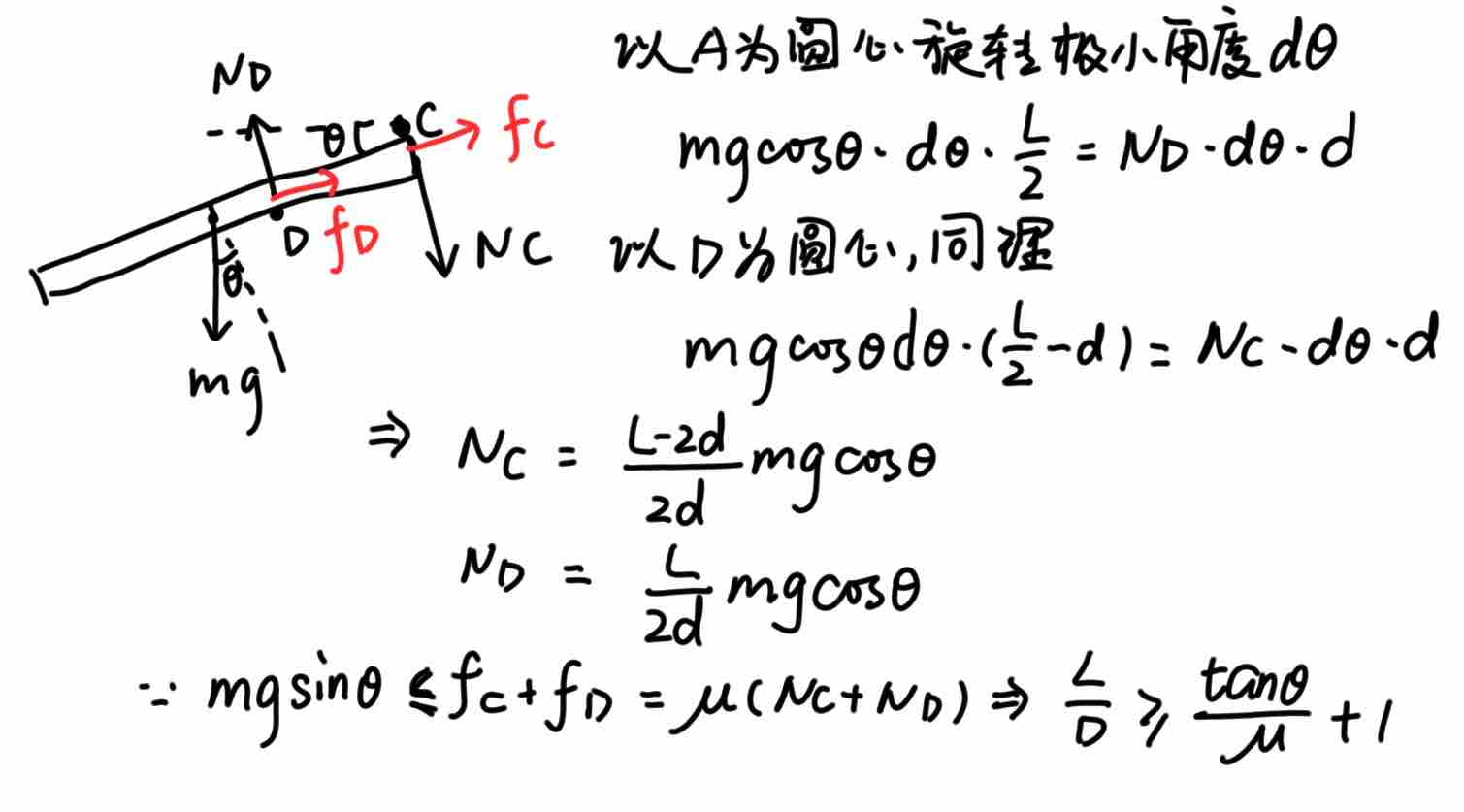
应用虚功原理,解答如下:
(这种情况下,约掉  后,虚功原理与力矩平衡方程是相同的)
后,虚功原理与力矩平衡方程是相同的)

JQX|Jin
【下期预告】
从一道小题的细节入手,从牛顿定律、动量定理和动能定理等角度解构非弹性碰撞,涉及形变、摩擦力的功、弹力的功···
On this day..
- *LEARN BETTER - 2020
- 以己为师 自求自得 - 2014
- 自由的灵魂 - 2005
- 谁的卷子这么潦草 - 2005
- 婚礼花絮 - 2004