十二 12

从麦克斯韦方程组到光速

研教|〖席明纳理〗 肖遥 2025

JQX/进取芯 席明纳第22期（2025.12.09）

从麦克斯韦方程组到光速

JQX|Xiao

一、波动方程
对于一个机械波，想描述它在空间的分布，它的方程为： D(x) = A \sin \frac{2\pi}{\lambda} x 。如果这个机械波以速度 v 向右传播，则 t 时刻的波函数为： D(x,t) = A \sin \left[ \frac{2\pi}{\lambda} (x - vt) \right] ，引入周期 T 可变形为： D(x,t) = A \sin \left( \frac{2\pi x}{\lambda} - \frac{2\pi t}{T} \right) 。
简化为： D(x,t) = A \sin (kx - \omega t)
其中 k = \frac{2\pi}{\lambda} ，称为波数。由此得到波的传播速度为： v = \lambda f = \left( \frac{2\pi}{k} \right) \left( \frac{\omega}{2\pi} \right) = \frac{\omega}{k}

二、麦克斯韦方程组
麦克斯韦方程组包含以下四个方程：
1. \oint \vec{E} \cdot d\vec{A} = \frac{Q}{\epsilon_0}
2. \oint \vec{B} \cdot d\vec{A} = 0
3. \oint \vec{E} \cdot d\vec{l} = - \frac{d\Phi_B}{dt}
4. \oint \vec{B} \cdot d\vec{l} = \mu_0 I + \mu_0 \epsilon_0 \frac{d\Phi_E}{dt}
其中第一个是电场的高斯定律，第二个公式说明了磁场无源，第三个是法拉第电磁感应方程，第四个是一般形式的安培环路定律。前面三个我们都比较熟悉，下面我们对第四个方程进行一下解释：
安培环路定律的一般形式为： \oint \vec{B} \cdot d\vec{l} = \mu_0 I 。但是科学家们发现了这样的矛盾：假设有一个平行板电容器连着两根导线，正在充电。我们对其中一根导线取一个高斯环路，可以求出它的磁场环路积分。但是现在的问题是等式右面的电流 I 应该怎么选择？

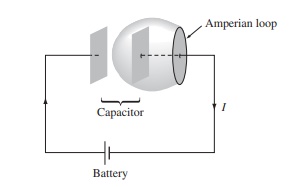
我们认为电流是指“通过环路所围成的截面”的电流。但是这个截面我们可以任意选择：比如我们可以选择一个平面使这个导线穿过它；或者选取一个曲面，**就像吹起的泡泡糖**，让它把电容器的一个极板包含进去。这样我们发现一个问题：选的第二个曲面（泡泡糖）并没有电流穿过它，但是我们明明选取的高斯环路没有变，也就是说虽然没有电流，但是等式右边一定有什么东西**替代**了这个电流。我们把这个电流叫做**位移电流**。

根据高斯定律： \Phi_E = E \cdot A = \frac{Q}{\epsilon_0} ，我们对它求导可以得到： \frac{d\Phi_E}{dt} = \frac{1}{\epsilon_0} \frac{dQ}{dt} = \frac{1}{\epsilon_0} I 。

得到电流大小： I_d = \epsilon_0 \frac{d\Phi_E}{dt} ，我们称这个电流大小为位移电流，它反应了电场的变化会产生磁场。空间中的磁场可以由两部分产生，一部分由电流产生，一部分由变化的电场产生。当空间中既有电流，又有变化的电场，就是如下的表述形式： \oint \vec{B} \cdot d\vec{l} = \mu_0 (I + I_d) = \mu_0 I + \mu_0 \epsilon_0 \frac{d\Phi_E}{dt}

三、麦克斯韦方程组推导光速
1. 麦克斯韦方程组（真空环境）。先考虑真空中没有电荷 ( Q=0 ) 和电流 ( I=0 )。这时麦克斯韦方程组的积分形式如下：
1. 电场高斯定律： \oint \vec{E} \cdot d\vec{A} = 0
2. 磁场高斯定律： \oint \vec{B} \cdot d\vec{A} = 0
3. 法拉第电磁感应定律： \oint \vec{E} \cdot d\vec{l} = - \frac{d\Phi_B}{dt}
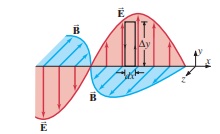
4. 安培-麦克斯韦定律： \oint \vec{B} \cdot d\vec{l} = \mu_0 \epsilon_0 \frac{d\Phi_E}{dt}
2. 建立一阶偏微分关系：假设电磁波沿 x 轴传播，电场 E 沿 y 轴，磁场 B 沿 z 轴，即 E = E_y = E_0 \sin(kx - \omega t) 和 B = B_z = B_0 \sin(kx - \omega t) 。
利用法拉第定律计算电场等式左右两边，可得： \frac{\partial E}{\partial x} = - \frac{\partial B}{\partial t} —— (式 1)
利用安培-麦克斯韦定律（选取 xz 平面回路）：
计算磁场环路积分与电通量变化率（位移电流），可得： - \frac{\partial B}{\partial x} = \mu_0 \epsilon_0 \frac{\partial E}{\partial t} —— (式 2)

3. 代入波动方程
计算电场和磁场对空间 x 和时间 t 的偏导数：
\frac{\partial E}{\partial x} = k E_0 \cos(kx - \omega t) 且 \frac{\partial E}{\partial t} = -\omega E_0 \cos(kx - \omega t)
\frac{\partial B}{\partial x} = k B_0 \cos(kx - \omega t) 且 \frac{\partial B}{\partial t} = -\omega B_0 \cos(kx - \omega t)
4. 比较系数
代入法拉第定律关系式：
由 \frac{\partial E}{\partial x} = - \frac{\partial B}{\partial t} ，代入可得： k E_0 \cos(\dots) = - [-\omega B_0 \cos(\dots)] 。化简得： k E_0 = \omega B_0 ，整理得到： \frac{E_0}{B_0} = \frac{\omega}{k} = v
由 - \frac{\partial B}{\partial x} = \mu_0 \epsilon_0 \frac{\partial E}{\partial t} ，代入安培定律关系式可得： - k B_0 \cos(\dots) = \mu_0 \epsilon_0 [-\omega E_0 \cos(\dots)] 。化简得： k B_0 = \mu_0 \epsilon_0 \omega E_0 ，整理得： \frac{E_0}{B_0} = \frac{k}{\mu_0 \epsilon_0 \omega}
联立求解： v = \frac{k}{\mu_0 \epsilon_0 \omega} = \frac{1}{\mu_0 \epsilon_0 (\omega/k)} = \frac{1}{\mu_0 \epsilon_0 v} 即： v^2 = \frac{1}{\mu_0 \epsilon_0}
解得： v = \frac{1}{\sqrt{\mu_0 \epsilon_0}} = c \approx 3.00 \times 10^8 \text{ m/s}

On this day..

Comments are closed.