JQX/进取芯 席明纳第21期(2025.11.20)

高斯定理的简单应用

JQX|Jin
一、磁通量,电通量
磁通量指的是穿过某一面积的磁感线总数,是描述磁场分布情况的物理量,其大小等于磁感应强度与垂直于磁场方向的面积的乘积。电通量则表示穿过某一面积的电场线总数,反映电场的分布特征,二者均为标量,但具有正负之分,体现场线穿入与穿出的方向关系。
在计算时,若场强与面不垂直,则需将面积投影到与场强垂直的方向,或分解场强进行相应运算。磁通量的表达式是  ,电通量的表达式则为
,电通量的表达式则为  ,
,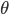 为电场方向与面积法线方向的夹角。
为电场方向与面积法线方向的夹角。
二、磁场和电场的另一种表述形式
根据磁通量的定义,单位面积的磁通量即为磁感应强度,即  ,所以磁感应强度还有一个名字:磁通量密度。 同理,单位面积的电通量也对应电通量密度(电位移矢量
,所以磁感应强度还有一个名字:磁通量密度。 同理,单位面积的电通量也对应电通量密度(电位移矢量  ,我们讨论真空中
,我们讨论真空中  ),满足如下关系:表征电场在该点的强弱与作用方向。
),满足如下关系:表征电场在该点的强弱与作用方向。
三、高斯定理
用正点电荷举例。以正点电荷为中心作一闭合球面,电场线从电荷出发垂直穿出球面,穿过该闭合曲面的电通量为  。
。
根据库仑定律  ,代入得
,代入得  。这其中我们定义
。这其中我们定义  ,
, 为真空介电常数。有
为真空介电常数。有  。
。
这表明真空中静电场通过任意闭合曲面的电通量等于其包围电荷量的代数和除以真空介电常数,即电场高斯定理:  请注意,这里的积分符号上有一个小圈,表示闭合曲面上的积分。
请注意,这里的积分符号上有一个小圈,表示闭合曲面上的积分。
现阶段,为了方便计算,我们在选取高斯面时应清楚电荷的分布,确保高斯面形状利于对称性分析,常选球面、柱面或平面等特殊几何面,并使电场强度垂直于高斯面且在面上各点大小相等,从而将电场强度  提到积分符号外,直接使
提到积分符号外,直接使  简化运算。
简化运算。
四、高斯定理的应用
一)无限长带电直线的电场
例1 设有一无限长均匀带电直线,电荷线密度为  。求距离直线为
。求距离直线为  处的电场强度。
处的电场强度。
方法一(高斯定理):如黑板中间左侧图,选取以带电直线为轴线、半径为  的闭合圆柱面作为高斯面,其侧面与电场方向垂直,两底面与电场平行(无电场穿过),因此电通量为
的闭合圆柱面作为高斯面,其侧面与电场方向垂直,两底面与电场平行(无电场穿过),因此电通量为  。
。
高斯面内包围的电荷量为  ,由高斯定理
,由高斯定理  得
得  ,化简得
,化简得  。
。
这表明无限长均匀带电直线周围电场强度与距离成反比,方向沿径向向外(正电荷)或向内(负电荷),具有轴对称性。
方法二:利用电场叠加原理,将带电直线视为无数点电荷的集合,取微元  ,结合库仑定律计算其在场点产生的电场
,结合库仑定律计算其在场点产生的电场  ,再对整条直线积分。这个积分式我们不易求解,这里介绍一个巧妙的投影方法:
,再对整条直线积分。这个积分式我们不易求解,这里介绍一个巧妙的投影方法:
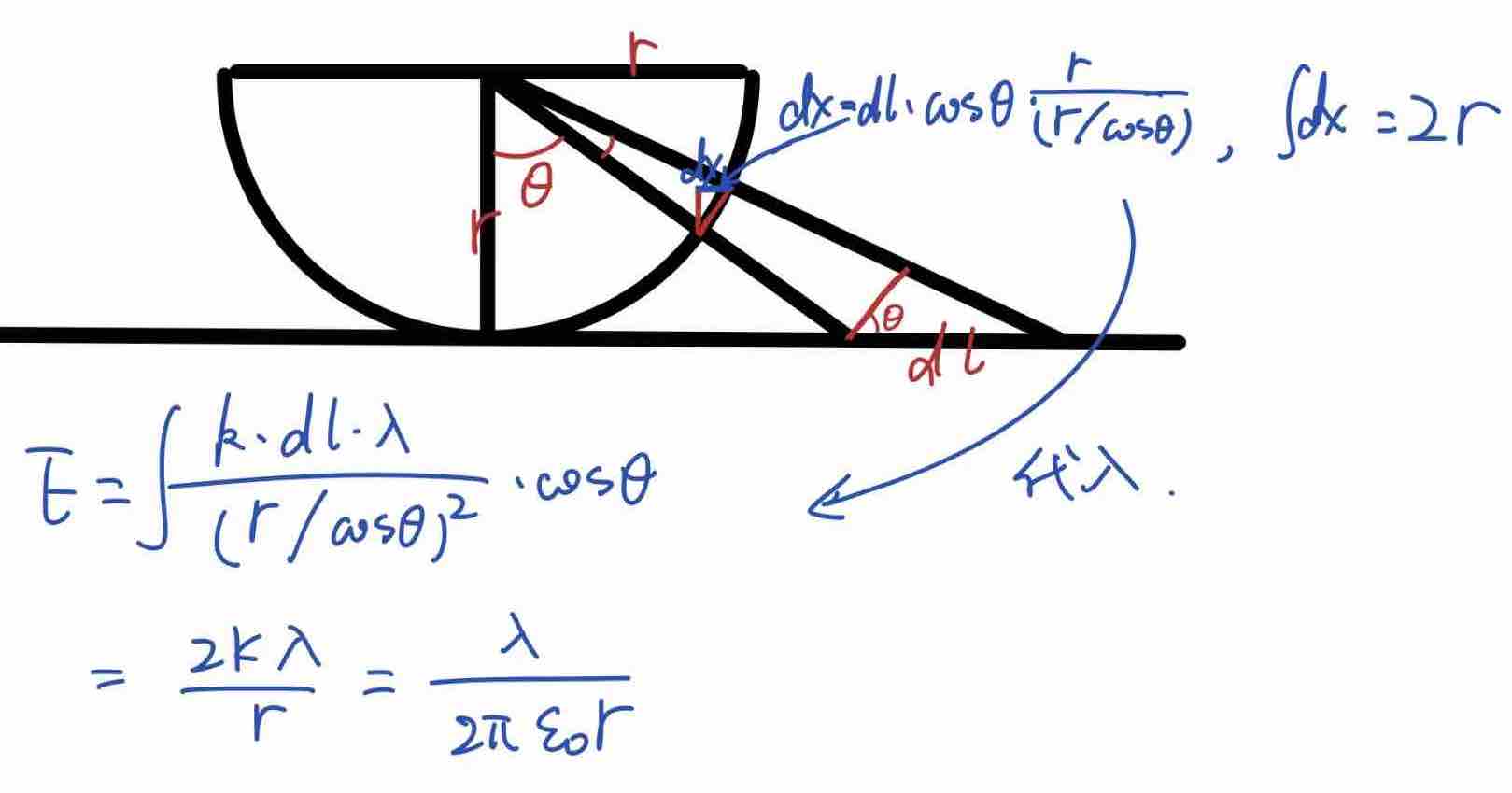
反过来,如果我们要求半圆形带电体(均匀,电荷线密度也为  ),可以用同样的方法进行积分,可证半圆形带电体在圆心处产生的电场强度与相同电荷密度的无限长带电直线在距其
),可以用同样的方法进行积分,可证半圆形带电体在圆心处产生的电场强度与相同电荷密度的无限长带电直线在距其  处产生的电场相同。
处产生的电场相同。
二)无限大均匀带电平面的电场
例2 设有一无限大均匀带电平面,电荷面密度为  ,求距离平面为
,求距离平面为  处的电场强度。
处的电场强度。
选取一垂直于平面的闭合圆柱形高斯面,两底面平行于带电平面且对称分布,面积均为  ,侧面与电场方向平行。由于电场方向垂直于平面,故无电通量穿过侧面,而两底面处电场大小相等、方向与法线同向,总电通量为
,侧面与电场方向平行。由于电场方向垂直于平面,故无电通量穿过侧面,而两底面处电场大小相等、方向与法线同向,总电通量为  。
。
高斯面内包围电荷量为  ,由高斯定理
,由高斯定理  得
得  ,化简得
,化简得  。这表明无限大均匀带电平面两侧电场为匀强电场,方向垂直于平面向外(正电荷)或向内(负电荷)。
。这表明无限大均匀带电平面两侧电场为匀强电场,方向垂直于平面向外(正电荷)或向内(负电荷)。
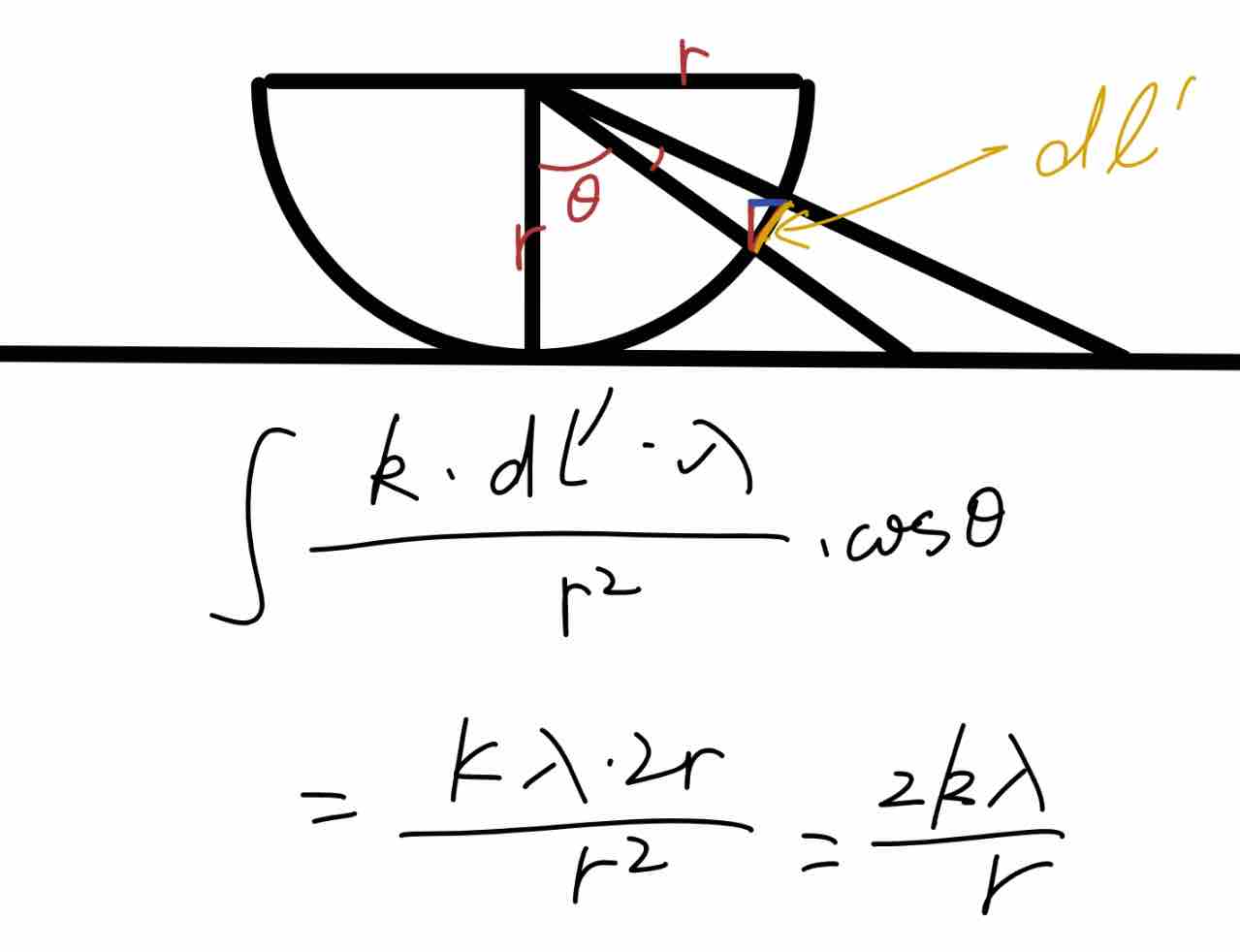
【讨论】类比例1的方法二,利用投影的方法,能否可以把无限大平面投影到半球上?
这种等效法是把均匀带电平面上的面元在球心产生的电场强度沿轴线方向的分量与均匀带电半球面上的面元在球心产生的电场强度的大小(不考虑方向)进行等效,但此时的平面与半球面并不完全等效。从矢量叠加效果而言,均匀带电无限大平面在空间某点产生的场强大小并不等于以该点为球心且与平面相切的均匀带电的半球面在球心产生的场强大小。
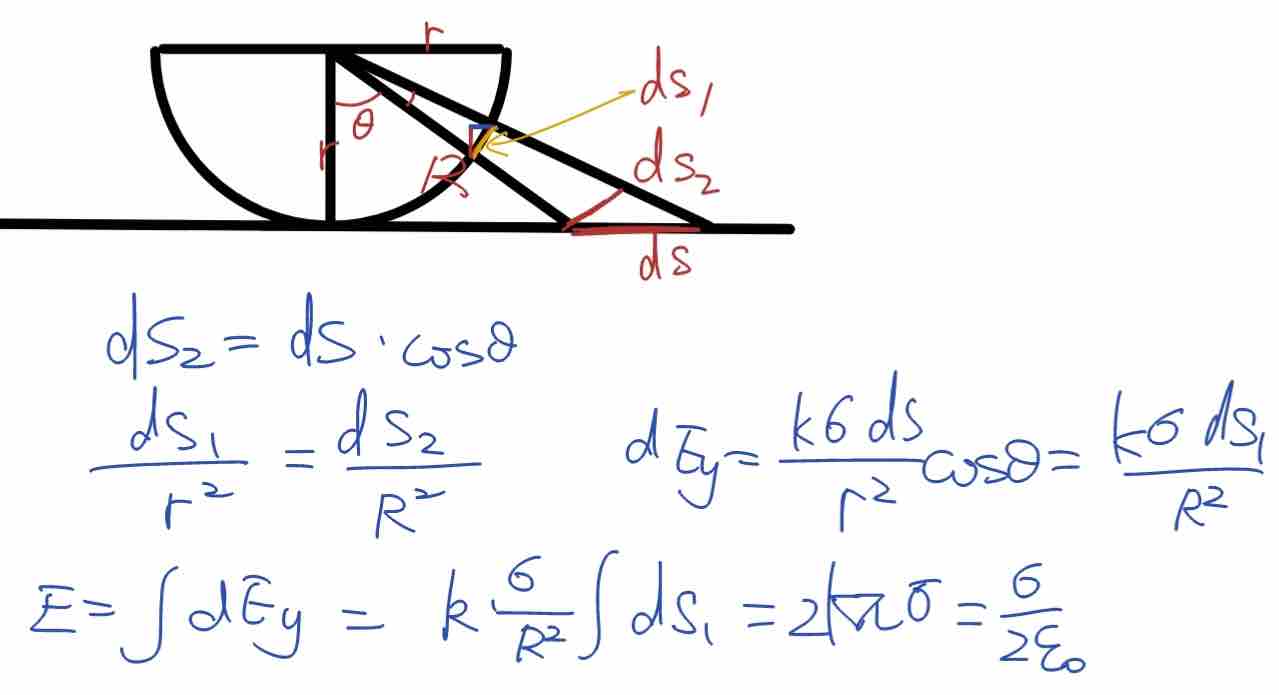
下面我们来求解均匀带电的半球面在球心产生的场强大小。
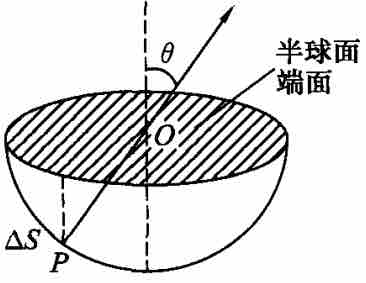
如图所示,设半径为  的均匀带电的半球面电荷面密度为
的均匀带电的半球面电荷面密度为  ,球心为
,球心为  点。
点。
在球面上任意取一点  ,选一图中面元
,选一图中面元  ,半径
,半径  与对称轴的夹角为
与对称轴的夹角为  ,面元
,面元  所带电荷量为
所带电荷量为  ,当
,当  足够小时,
足够小时, 可视为点电荷。
可视为点电荷。
设  在球心处产生的场强为
在球心处产生的场强为  ,则
,则  。
。
由对称性可知,只有  沿对称轴方向的分量对球心处的合场强有贡献,其大小为
沿对称轴方向的分量对球心处的合场强有贡献,其大小为  。
。
因  是
是  在半球面端面方向上的投影面积,设为
在半球面端面方向上的投影面积,设为  ,则
,则  。
。
这个表面上的电荷在球心处的场强即该面上所有  上电荷在球心场强的叠加,所以得
上电荷在球心场强的叠加,所以得
而  表示半球面在端面上的投影的面积即端面的面积,
表示半球面在端面上的投影的面积即端面的面积, 。
。
所以均匀带电半球面在球心产生的场强大小为  ,而无限大平面产生的场强大小为
,而无限大平面产生的场强大小为  ,二者结果相差二倍。[1]
,二者结果相差二倍。[1]
三)均匀带电球壳的电场
例3 一半径为  的均匀带电球壳,总电荷量为
的均匀带电球壳,总电荷量为  ,计算球壳内外电场。
,计算球壳内外电场。
当计算求外电场( )时,我们选取半径为
)时,我们选取半径为  的同心球面作为高斯面,由对称性知电场沿径向且在球面上大小处处相等,电通量
的同心球面作为高斯面,由对称性知电场沿径向且在球面上大小处处相等,电通量  。包围电荷为
。包围电荷为  ,由高斯定理得
,由高斯定理得  ,等效于点电荷电场。
,等效于点电荷电场。
当计算球内电场( )时,高斯面内无电荷,故
)时,高斯面内无电荷,故  。这表明均匀带电球壳内部场强为零,外部场强分布与点电荷相同。
。这表明均匀带电球壳内部场强为零,外部场强分布与点电荷相同。
四)均匀带电实心球体的电场
例4 一半径为  的均匀带电实心球体,电荷体密度为
的均匀带电实心球体,电荷体密度为 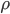 ,总电荷量为
,总电荷量为  ,计算球内外电场。
,计算球内外电场。
当计算球外电场( )时,选取半径为
)时,选取半径为  的同心球面作为高斯面,由球对称性可知电场沿径向且在球面上大小处处相等,电通量
的同心球面作为高斯面,由球对称性可知电场沿径向且在球面上大小处处相等,电通量  。高斯面内包围电荷量为
。高斯面内包围电荷量为  ,由高斯定理得
,由高斯定理得  ,等效于点电荷电场。
,等效于点电荷电场。
当计算球内电场( )时,高斯面内包围电荷量为
)时,高斯面内包围电荷量为  ,代入高斯定理得
,代入高斯定理得  ,化简得
,化简得  。
。
这表明均匀带电实心球体内部电场随距离线性增大,方向沿径向向外(正电荷)或向内(负电荷),而在球外则等效于全部电荷集中于球心的点电荷电场,整体呈现球对称性。
五)平行板电容器决定式的推导
设两平行金属板带等量异种电荷,电荷量为  。我们可以取一个长方体高斯面,包裹住其中一个金属板。
。我们可以取一个长方体高斯面,包裹住其中一个金属板。
由高斯定理得可得  ,其中包围的电荷量为
,其中包围的电荷量为  ,且
,且  ,结合
,结合  ,代入得
,代入得  。
。
如果有介质填充,则电容变为  。
。
六)均匀带电球体,中间挖空,求挖空部分的电场强度
这个题目的结论很有趣:匀强电场,场强与两球球心连线为半径的带电球产生的电场相同。
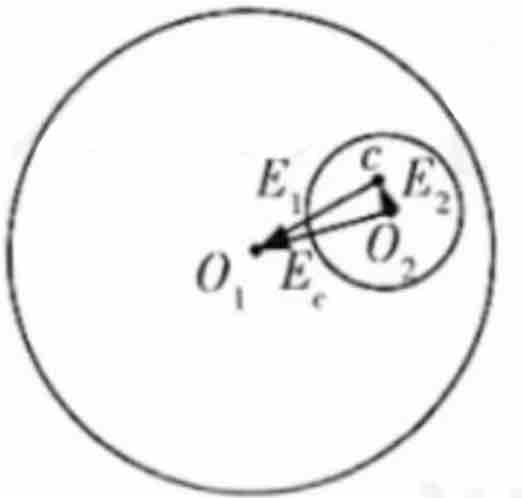
设球体单位体积带电荷量为 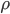 ,挖去小球后该带电体可等效为一个带电荷量为
,挖去小球后该带电体可等效为一个带电荷量为  的带负电大球和一个带电荷量为
的带负电大球和一个带电荷量为  的带正电小球,空腔内任一点的场强就是这两个带电球在该点产生的场强的矢量和,如图所示。
的带正电小球,空腔内任一点的场强就是这两个带电球在该点产生的场强的矢量和,如图所示。
设等效大球在  点产生的电场强度大小
点产生的电场强度大小  ,方向由
,方向由  指向
指向  ;同理,等效小球
;同理,等效小球  在
在  点产生的电场强度大小
点产生的电场强度大小  ,方向由
,方向由  指向
指向  。
。
由矢量运算法则与三角形相似,可得  点的电场强度方向由
点的电场强度方向由  指向
指向  ,
, 点电场强度
点电场强度  。
。
综上分析可知:空腔内各点电场强度大小相等、方向相同(由  指向
指向  ),即为匀强电场。
),即为匀强电场。
七)带电球壳,求其中一小块处的场强
根据静电屏蔽,其他部分和这小块在此处产生的总电场为0,所以求解这一块产生的电场即可。
选取与小块面积相同底面积的小圆柱为高斯面,由于对称性,圆柱侧面没有电场线穿过,外底面有电场穿过,内底面电场为0,根据高斯定理:
可求得这一小块电场强度为:
【参考文献】[1]郑金.均匀带电无限大平面与半球面电场的等效问题[J].物理教师,2013,34(06):19-20.
【下期预告】光速是怎么推出来的?与波动方程是什么关系?下起我们共同探讨由麦克斯韦方程组推导出波动方程。
On this day..
- 伴你长大 - 2023
- The Aims of Education - 2021
- 予力众生 成就不凡 - 2018
- 每一口井都曾是一个奢侈的家 - 2012
- 电平衡 - 2008
- 智慧型教师 - 2006
- 校园八大天地 - 2005
- 广东顺德行5 - 2004
- 亮 一直在自己的手中 - 2003