斜抛运动的最远距离

九 26

斜抛运动的最远距离

研教|〖席明纳理〗金庆辰 2025

JQX/进取芯席明纳第15期（2025.9.17）

斜抛运动的最远距离

JQX|Jin
一、平抛结论的斜抛延伸
平抛有两个二级结论：
1. 某点速度的反向延长线过水平位移中点
提示：通过速度角、位移角正切值关系证明。
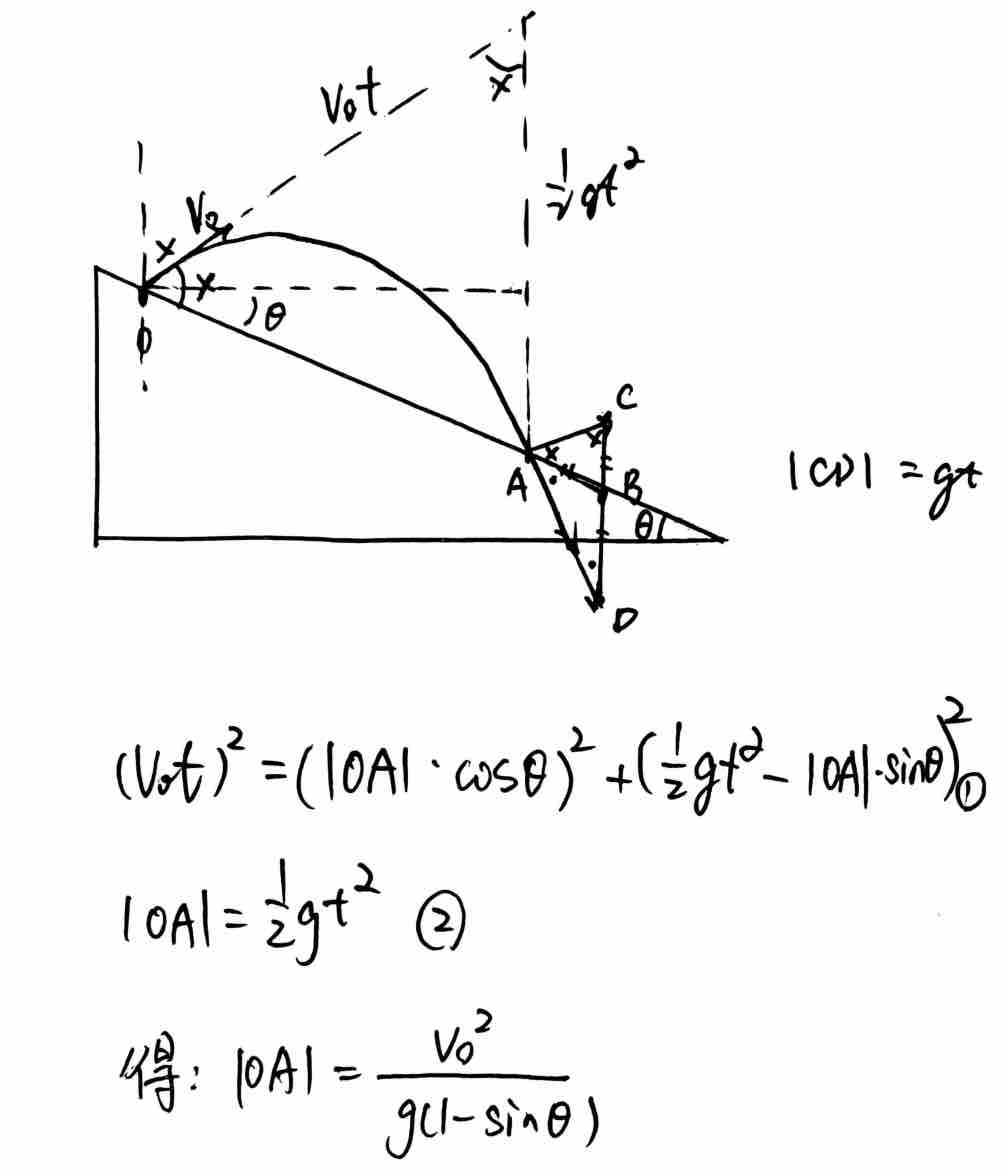
2. 某点位移的延长线过竖直分速度的中点（如黑板图1）
- 法一：通过三角形相似，结合速度角、位移角正切值关系证明。
- 法二：qiusir 提出了一个平均速度法（帅）。平均速度的定义是

$\vec{v} = \frac{\vec{x}}{t}$ ，这是一个矢量式，也告诉我们位移的方向与平均速度的方向相同。竖直方向上，平均速度为

$\frac{gt}{2}$ ，所以在这个方向上过竖直位移中点。
那么，在斜抛运动中，这两个条件是否成立？
成立，但有一个前提：我们要将斜抛运动沿初速度方向和竖直方向斜交分解。此时运动变为沿初速度方向的匀速直线运动和自由落体运动，在这个分解方法下，两个二级结论依然成立，证明方法与平抛运动相同。
二、向地面斜抛的最远距离
当离地高度

$h$ 一定，以某一大小确定的速度抛出小球，求角度为多少时射程最远，射程为多少？
最基本的方法是假设角度，列出射程与角度的函数解析式，求极值。
这里讲解一个三角形面积法：
- 射程的表达式：

$x = v_0 t \cos\theta$
- 落点速度矢量三角形的面积：

$s = v_0 \cos\theta \cdot gt$
- 由上两式可得：

$s = gx$
因此，矢量三角形面积最大时，射程最大。
根据动能定理，小球落地时末速度大小确定（因初速度大小为定值），则**末速度与初速度垂直时**，速度三角形面积最大，射程也最大。
确定方向后，可根据初末速度大小求出矢量三角形面积，进而求最大射程。
三、从斜面上斜抛的最远距离
以某一大小确定的速度从斜面上某点抛出小球，求角度为多少时射程（落到斜面上）最远，射程为多少？
- 法一：解析式法
解析式法依然可解，但计算难度较大。
- 法二：三角形面积法与关键结论
三角形面积法可用，依然满足

$s = gx$ （

$x$ 为射程的水平位移），但需讨论：本题末速度大小不确定，射程最大时，是否依然为初末速度方向垂直呢？
我的证明思路（较复杂）：
对于速度三角形，沿位移方向连接

$AB$ ，根据结论（前文平抛延伸的二级结论），

$B$ 为

$CD$ 中点，则

$\triangle ABC$ 的面积为

$\triangle ACD$ 的一半。又因

$AC$ 大小确定、

$\angle ABC$ 角度大小确定，根据几何关系（用圆周角证明），当

$AB = BC$ 时面积最大，射程也最大（如图中所有“×”角相等）。
由此可得到结论：**当入射方向为竖直与斜面的角分线方向时，射程最大**。
同理，图中两个“·”角也相同，则

$\angle CAD$ 为直角。
肖老师和qiusir的巧妙观点：
假想某一落点为射程最远点，该点与出发点的高度差为某一定值（因假想点确定），则该落点对应的速度应满足“向地面斜抛最远距离”的结论（末速度与初速度垂直）。
斜面上任意一个落点，都有与之对应的高度

$h$ 下斜抛最远的速度角度关系（但该角度不一定是唯一解，因其他

$h$ 对应的角度也可能落到该点）；当

$h$ 最大时，有且仅有一组解，此即为射程最大点，故末速度与初速度必垂直。
有了角度关系后，再根据位移几何关系（利用斜交分解）可求得最远射程，计算难度不大(见图片）。

后记1：包络线法
为准备本节课内容，我最初研究了“基本运算”和“三角形面积”两种方法，已觉完善；但后续qiusir发给我俊豪β同学的抛体运动题目，其中一题核心内容与我讲授的相同（默契十足），且俊豪要求用三种方法求解，这促使我进一步研究，得出第三种方法——包络线法。
包络线的定义：指与给定曲线族中的每一条曲线至少在某一点相切，且在该点附近与曲线族中相邻曲线保持密切接触的曲线，可理解为“一簇曲线中最外侧点的连线”。

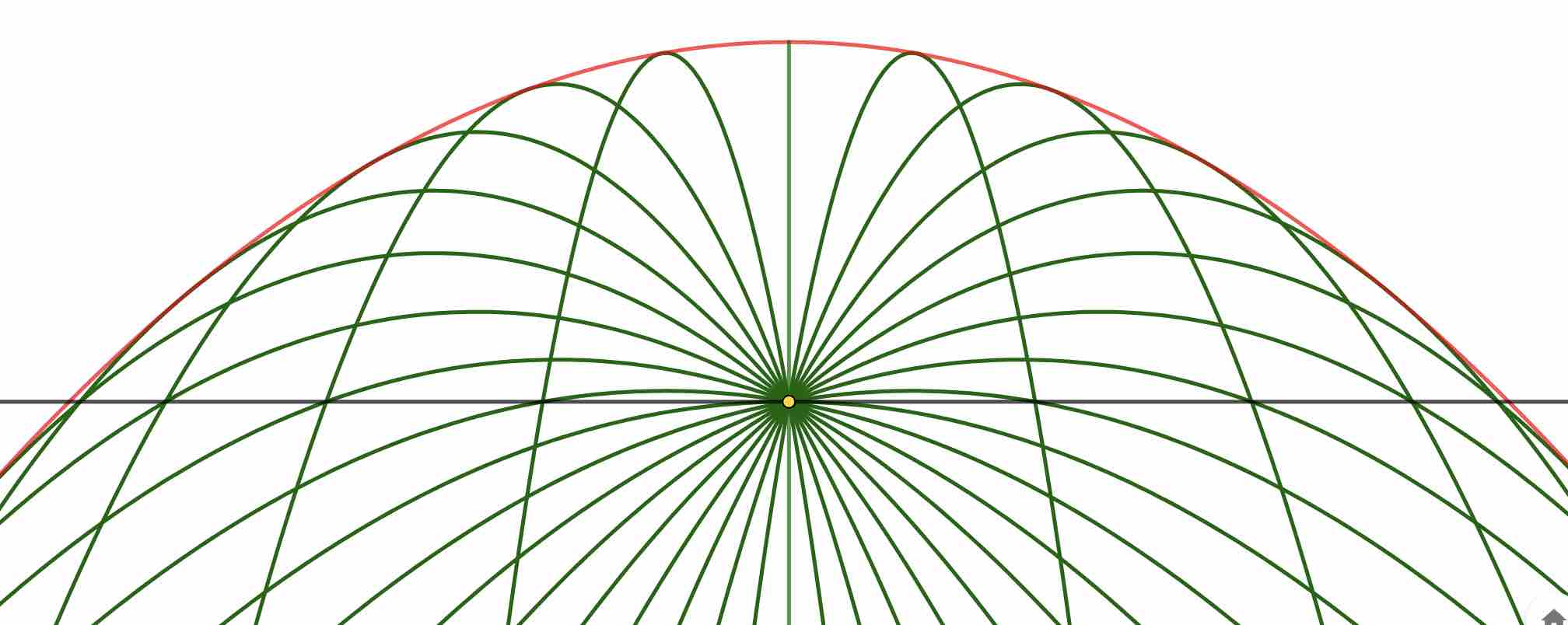
斜抛运动的包络线表达式：对于初速度大小恒定、方向任意的斜抛运动，包络线的表达式为

$y = -\frac{g}{2 v_{0}^{2}} x^{2} + \frac{v_{0}^{2}}{2 g}$

该表达式可通过“求所有确定

$x$ 对应的

$y$ 的最大值（以

$\tan\theta$ 为变量）”推导得出（推导过程不难，请自行查阅资料）。
利用包络线法求斜抛最远距离：求解包络线与斜面的交点，该交点对应的射程即为最大射程。

后记2：张耘铭原创题目
课后，K2304班张耘铭同学原创了一道有趣的题目：
从某一平面斜抛一个带电小球，已知速度大小和方向，环境中存在一匀强电场（大小、方向可变，即小球运动的加速度未知，但为匀变速运动）。
(1) 试求其返回该平面时的最小速度。
(2) 若已知加速度大小为 $a$ ，速度与平面夹角为30度，求返回平面最小速度时的位移。
方法不唯一，请思考吧！

【下期预告】
硬核证明两点之间直线最短——变分法在高中物理中的简单应用

On this day..

Comments are closed.