



·[?]无穷递缩等比数列的物理题
《优雅的物理》艾蒂安·居永等 巴黎高等师范学院 https://blog.espci.fr/merveilleux (似乎无法访问)(这个也需要梯子)
埃菲尔铁塔为了在1889年(电磁波被发现的后一年)的世界博览会上独占鳌头:建设一个超越千尺的铁塔,体现工程师的果敢和工业革命的胜利。
莫迫桑评价:“这个用铁梯做成的瘦高金字塔,这个庞大的、丑陋的骨架,它的基座看起来像是为了撑起一座巨大的独眼巨人的纪念碑,但最后又以可笑而尖细的工厂烟囱半的形状草草收尾。”(被质疑常去那的餐厅,莫迫桑回应说这是唯一看不到铁塔的地方)
埃菲尔回应,“铁塔有其自身的美”,抵抗外力的要求与“和谐之美的隐含要求相吻合”,以及“建筑美学的第一原则即”一座纪念物的基本线条应当完美地适应它的目的。

(网上选了这张照片)
他发明了一种风洞---埃菲尔风洞
最初的设计已经体现了拓宽铁塔中心空间的想法。
“让我们在地上和浪头嬉戏,那些出名的人多煎熬!世上的财富、名誉、虚假的荣耀,都不过是肥皂泡。”

皂液膜的厚度和光波的波长差不多,鲜艳华丽的彩虹色是因为不同厚度的皂液膜反射的相互干涉。
普拉托边界,为了纪念比利时物理学家Joseph Plateau,他曾面对日光研究视觉暂留,导致双目失明。
开尔文勋爵是定义泡沫结构的先驱,某种堆叠方式可以让肥皂泡的表面积最小。

多面体之间的接触点构成了定焦120°的三条棱,反映了表面张力造成的力平衡:为了减少水膜的表面积(此处表面积与棱长正比),表面张力以相同的力量分别向平面上的三个不同方向拉扯气泡。
Robert Hooke 是牛顿同时代的人,是天才的发明家(机械表上的游丝也是胡克发明的),命名了细胞,是试图在数学上定义悬链线的先驱。
在伦敦圣保罗大教堂的胡克纪念碑上,被称为“迄今为止世界上最有创造力的人之一。”

撑住桥的不是任何一块石头,马可回答,而是石块形成的桥拱。《看不见的城市》
任何事物,无论是以什么样的形式或物质彼此联结、存续,都有自己的时间。外形于是体现了生命的完整时间,以某种方式吞并过去,展示现在。《瓦雷利笔记》(贝壳、树干的年轮等)
蜘蛛网上均匀分布着黏性的小颗粒,可别和清晨凝结的露水混淆了。研究表明,这些小颗粒储藏了多余的环状蛛丝,收到冲击就会放线···小颗粒起到减震作用:猎物不会蹦出···
1801年织布机由里昂发明家发明,它的原理一只沿用到了现在。程序编制系统事实上启发了最早的计算机的发明。
我们歌颂不久前
英勇的孩子们之间的战争
在海滩上为保卫沙堡而战
这些不可逾越的壁垒
一个海浪就可以卷跑
混凝土,液体石头
公元前1世纪,哲学家卢克莱修想象物质的原子带有钩子,他们是相对坚固的。
开尔文勋爵和法拉第对形成雪花的冰晶的“烧结”很有兴趣。(雪球不会散架)
构成玻璃的矿物是完全无序的···那么玻璃是一种不为人知的液体吗?并不完全对。在分子层面,玻璃的结构的确和水的瞬间无序结构一致。但是,与被热运动持续搅动的液体不同,玻璃分子的这种无序在低温下冻结了。因此,在常温下,玻璃表现的和固体一样。
弯而不折的花颈
鲜切花中,细胞还包含水分,内压远远超过大气压,从而使花颈可以保持直立。
费曼因量子电动力学获得诺贝尔奖,他曾提出一根意大利面会断成几段的问题。(一根粉笔从不同高度下落会断成几段)
古希腊、古罗马时期人们因松树长青将其作为不死的象征。
德国的物理学家亥姆霍兹是描述摩擦琴弦发声机制的第一人。(马格努斯力跟数学谈不上关系,但他伟大的学生克劳修斯、亥姆霍兹等都没有继承他这种片面且无正当理由的物理学研究中数学使用的方式...)(开始研究物理学时,已经是19世纪最伟大的生理学家之一,而现在他是19世纪最伟大的物理学家之一了。他之后发现,不具备数学知识进行物理研究是不可能的,所以又开始研究数学,他现在还是19世纪中成就最高的数学家之一了。)(赫兹出生在汉堡,20岁在亥姆霍兹手下学习。)(普朗克在慕尼黑学习期间听了亥姆霍兹、基尔霍夫和维尔斯特拉的课程。)
蚁狮会在沙子上做一个倾斜的隧道,这里的牺牲者是蚂蚁。蚂蚁一旦误入歧途,便会从这个斜坡上不由自主地滑下去,然后被一阵乱石击死。
生菜叶上的几何学
数学家称这种俄罗斯套娃式的结构为分形结构。在撕裂的塑料袋中,我们可以发现有五代波浪,当波浪的大小和塑料膜的厚度相当时,塑料袋边缘会停止弯曲。
玻璃之泪一直以来都令人着迷,虽然看起来很纤弱,但它可以经受得住锤子的大力敲击。

1
微积分 预测未来变化的工具 [日]牛顿出版社编
速度=距离÷时间 微分的思考方式;距离=速度×时间 积分的思考方式
微分differential差别的,积分integral整体的;运算calculus拉丁语的小石头,过去人们是通过排列小石头来进行计算。
可以把函数想象为一个箱子,向其中输入一些东西,就会在箱子里进行某种计算,然后把结果吐出来。(只记得小时候老师花了很大的力气强调函数的重要性,但当时讲的什么是函数早没印象了)
极限思维是现代微积分的重点。(《无穷小》[?])
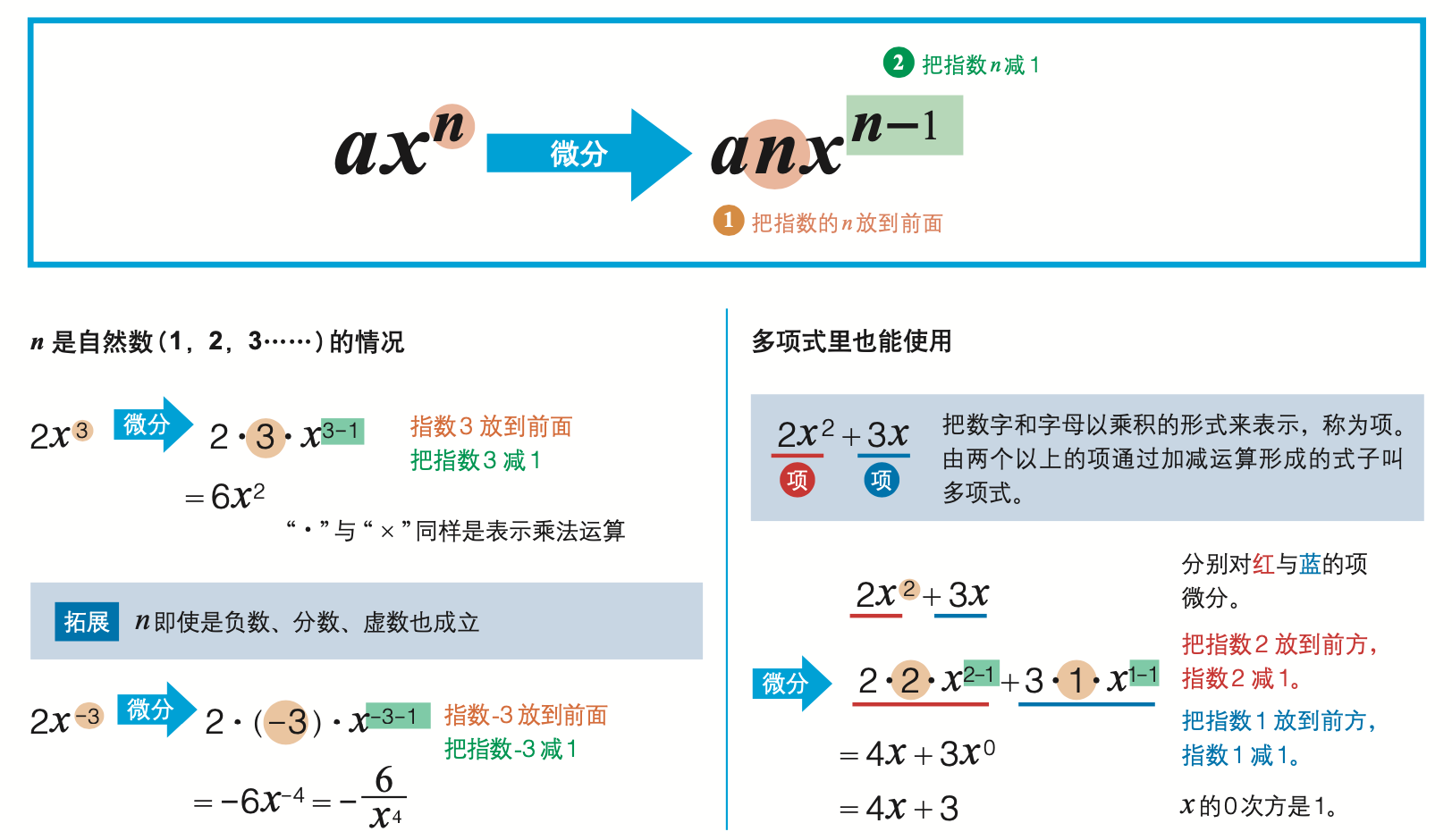
求导的过程又称为微分
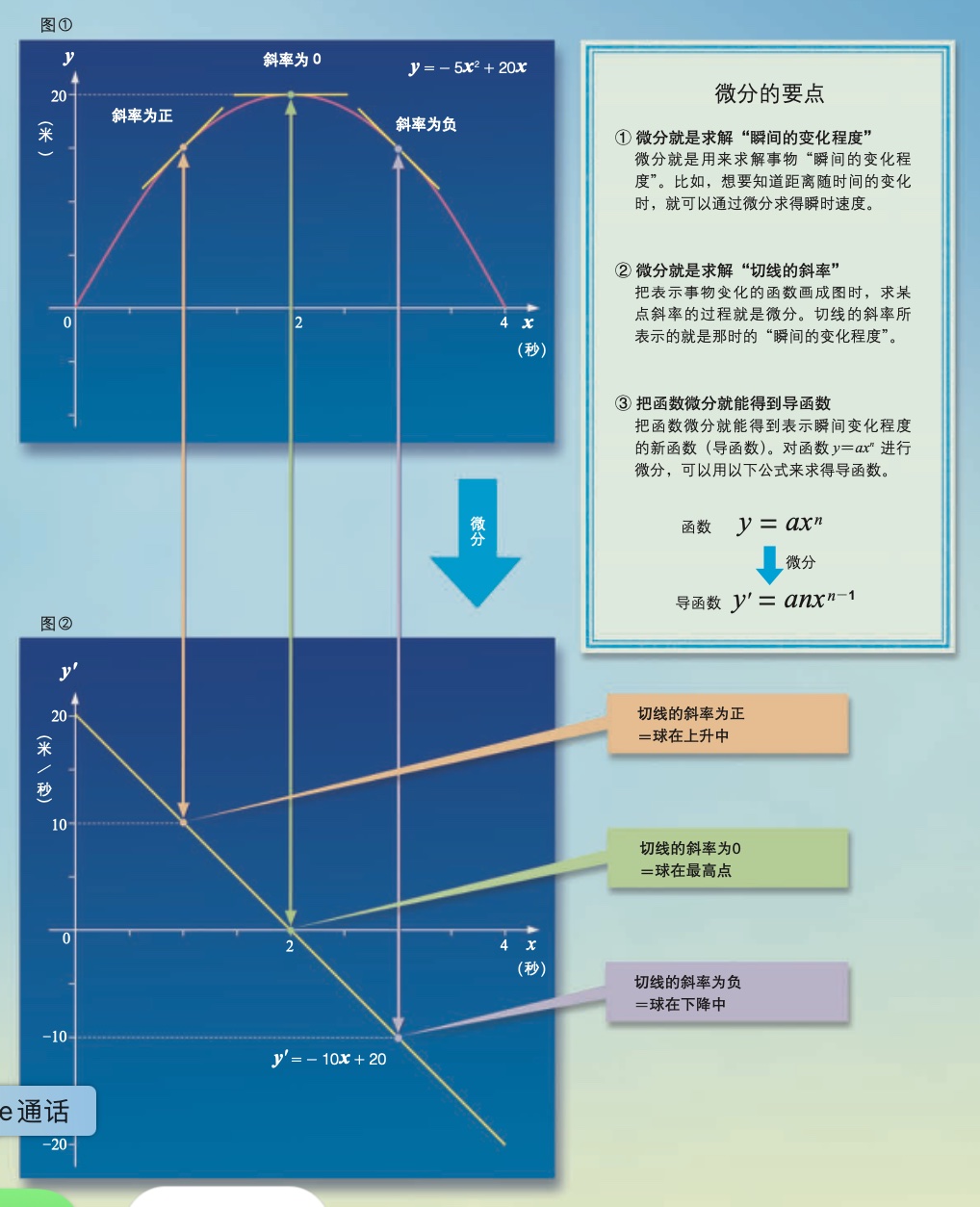
微分要点:微分就是求解“瞬间的变化程度”;微分就是求解“切线的斜率”;把函数微分就能得到导函数。
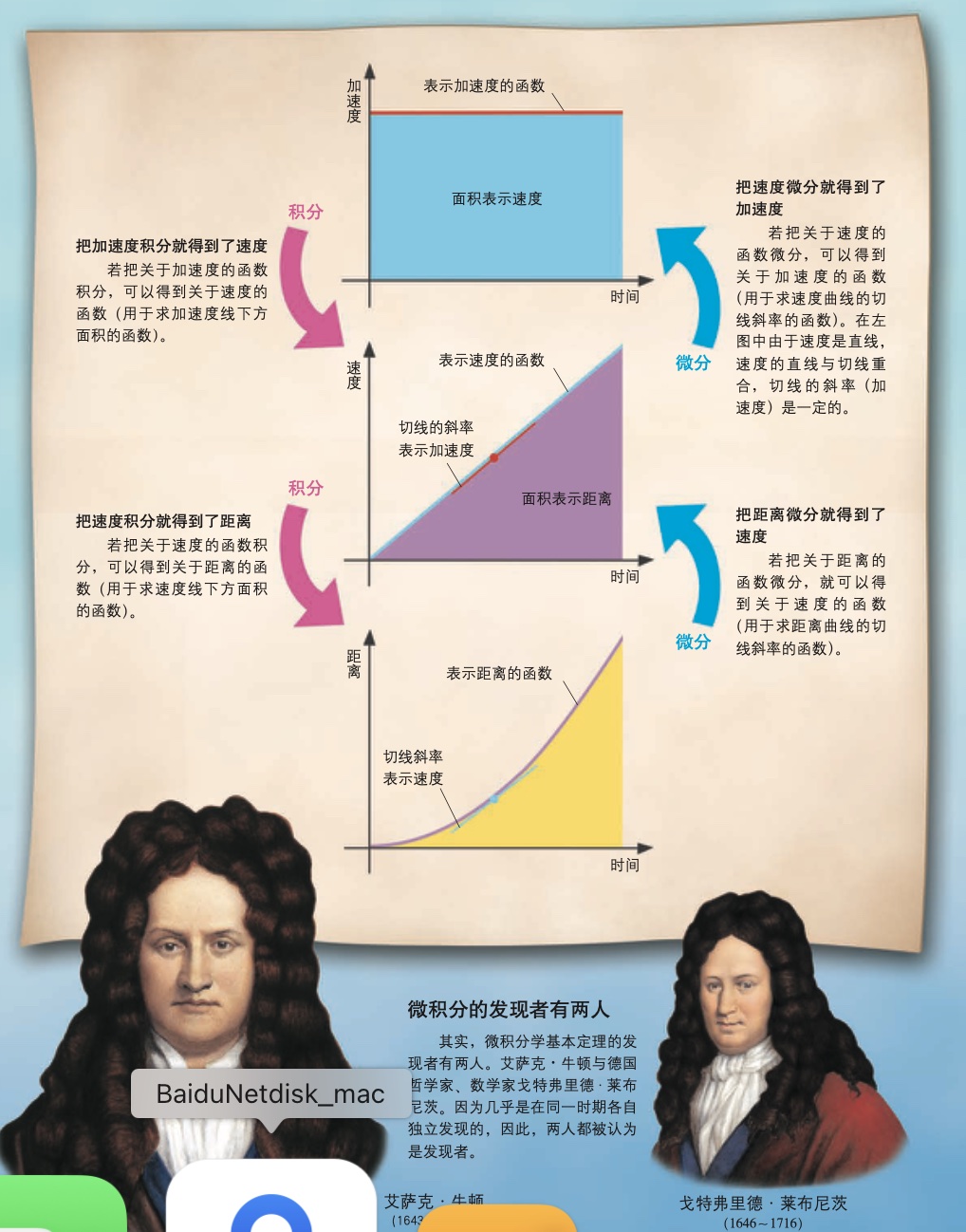
阿基米德把抛物线围成的面积分割成无数三角形求其面积和,用这样的穷竭法求得其面积。
牛顿发现了微分与积分其实是互逆的运算,把微分和积分统一为一门学问。
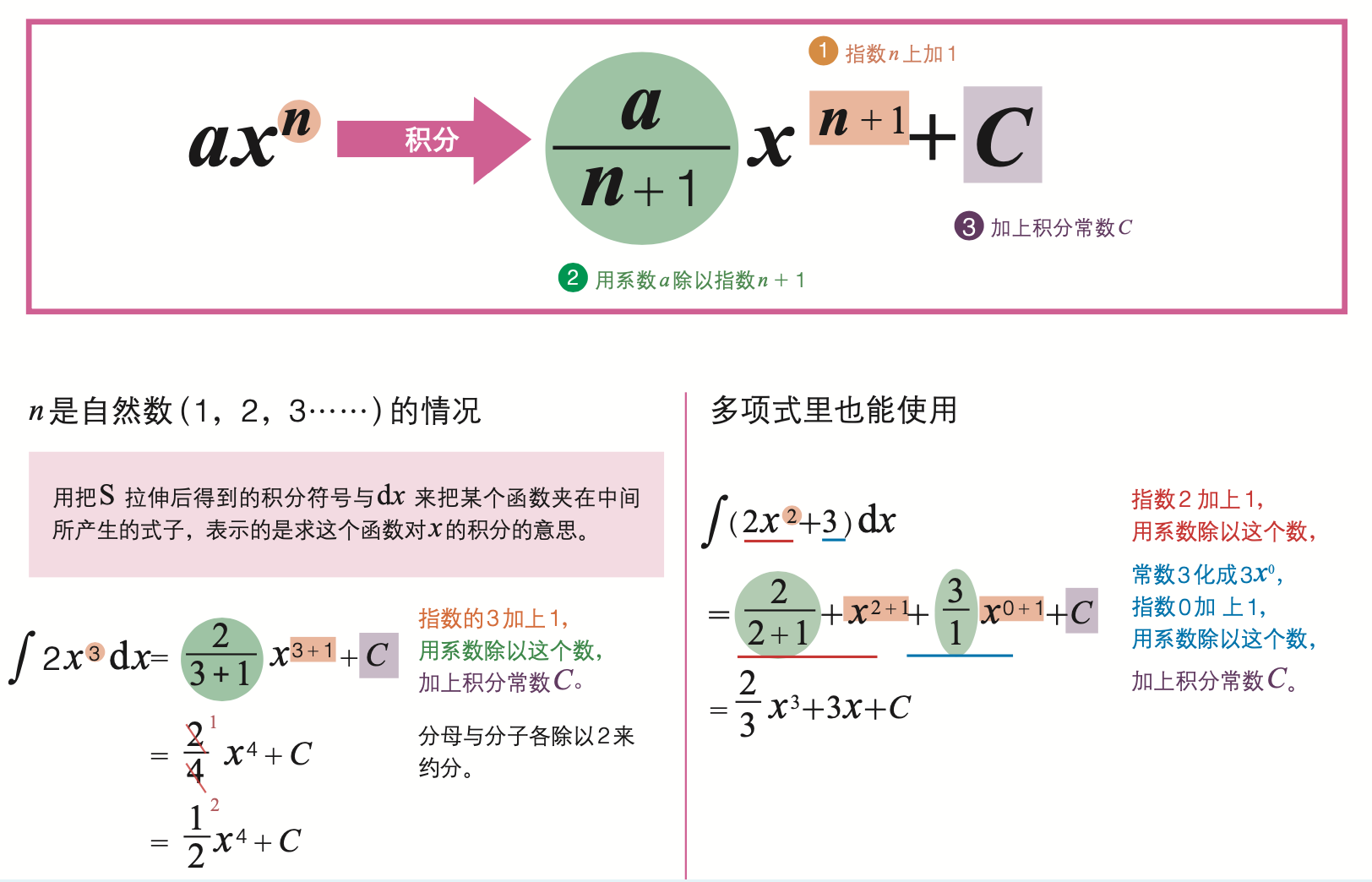
积分的要点:所谓积分就是求面积;积分有分割求积等方法;把函数积分可得原函数。
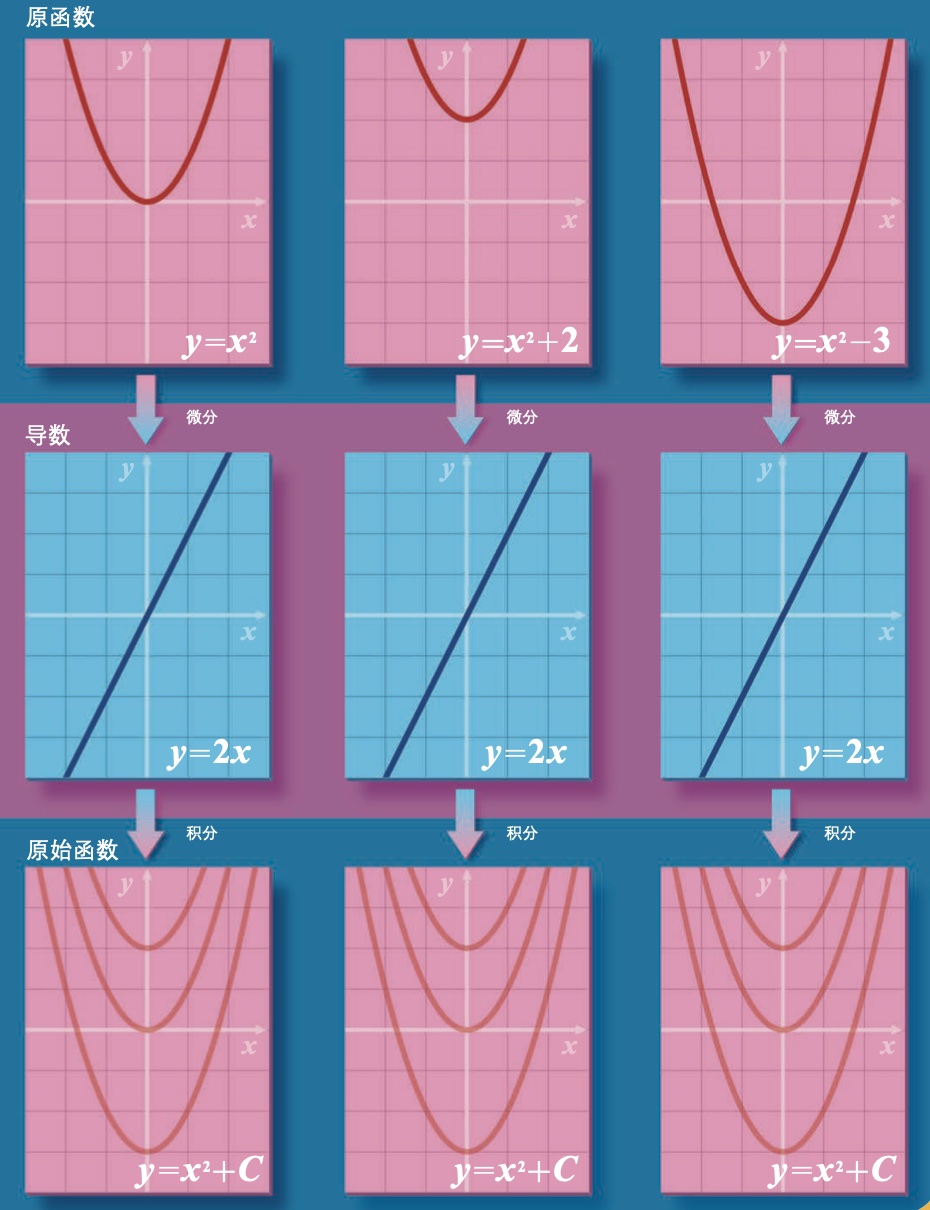
 这一符号整体是表示微分(导函数),而不是一个分数,读法也是"dydx"。先以differential(表示差的意思)来称呼微分的是莱布尼兹,dy和dx分别是y和x的微小增加量,所以d取的意思是differential的首字母。
这一符号整体是表示微分(导函数),而不是一个分数,读法也是"dydx"。先以differential(表示差的意思)来称呼微分的是莱布尼兹,dy和dx分别是y和x的微小增加量,所以d取的意思是differential的首字母。
 读作integral,整体,瑞士的雅各布·伯努利最先开始用这个词指代积分,想出这个符号的莱布尼茨。
读作integral,整体,瑞士的雅各布·伯努利最先开始用这个词指代积分,想出这个符号的莱布尼茨。
(圆周长 圆面积
圆面积 球表面积
球表面积 球体积
球体积 )
)
(应该推导一下球壳对球壳外万有引力等效于球心质点···
 )
)
1665年牛顿发现了微积分的基本定理,还是剑桥大学22岁的学生,记过确实40年后1704你啊发布;莱布尼兹发布的更早。有生之年那嫌疑都未曾被清洗。
匈牙利科学家冯诺依曼说微积分是“现代数学取得的第一个成就,对其重要性无论怎样评价都不为过。”
(伽利略的学生托里拆利不只是测量了大气压,这位意大利的数学家提出了被曲线围成区域的面积的求法。)

2
有人将阿基米德、牛顿和高斯并称世界三大数学家
Sir_Isaac_Newton_1689 时年46岁,为当时最有人气的肖像画家所做。
母亲希望牛顿停学务农,而且拒绝承担学费。(记得有书提到牛顿家的仆人觉得牛顿什么农活都干不好)
为了拿到奖学金参加资格考试,考官指出牛顿对于古希腊数学家欧几里得的知识掌握欠缺。牛顿只专心学习当时最先进的笛卡尔的理论。牛顿后来用于微积分发明(发现?)先关数学知识,便是从1664年前后阅读的书籍中积累起来的。可以说出了笛卡尔的《几何学》之外,英国的沃利斯《无穷算术》等作品也对牛顿的数学产生了极大影响。
牛顿的微积分原理、万有引力和光的理论,被称为“改变科学史的三大发现”。
牛顿正式开始数学研究1664年4月,仅仅数年,迅速超越了那个时期的数学水平,并独立创立了数学法则。(所以朗道单独把牛顿列为第0档)
牛顿执教超过30年,每周上一节课,课堂出席人数很少。
1727年,牛顿创立了calculus(微积分),也是因为calculus(结石)去世。享年84岁。

质疑固有观点,相信观测事实的“近代科学之父”伽利略
伽利略去世350年后的1992年,名誉才得以正式恢复。
笛卡尔和费马创立了坐标。坐标的引入将需要处理的现实世界中的现象变成了数学问题。
某天晚上,笛卡尔做了一个梦,在梦中他找到了科学的基础,解析几何学。
曲线的切线和运动物体的行进方向一致,由17世纪的法国数学家罗伯佛尔首先之初的。许多学者其实是把切线当作一个数学课题来进行研究的。
牛顿曾参考过费马找到的一种方法。
1664年,剑桥大学三年级学生牛顿开始阅读笛卡尔的著作。1665年产生了流数的思想,那一年22岁。
开普勒在第谷测得的大量火星数据的基础上,经过多次尝试并计算出火星的轨道。开普勒第二定律(面积定律)是早于第一定律(椭圆轨道)被创立。
以阿基米德为开端,积分方法在开普勒时代之后不断精炼,在伽利略的学生卡瓦列里和托里拆利的推动下,积分去的巨大成果。(卡瓦列里原理和中学学的祖暅原理)
亚里士多德提出,世界上一定由某种物质充满,否定了“真空”的存在。托里拆利完成了人类历史善跟第一次制造出真空。去世年仅39岁。
托里拆利小号
牛顿在1665年发现了积分是微分的逆运算。
哈雷(格林威治天文台的第二任台长;世界上第一个保险统计表和三次科学航海)根据微积分计算出彗星会在何时到来。
在英国皇家学会不当调查3年后莱布尼茨在愤懑中离世。
莱布尼茨发明机械计算器。
作为外交官的莱布尼兹在巴黎解释了克里斯蒂安·惠更斯。
莱布尼茨创立柏林科学院,担任首任会长。
效力的公爵为参选国王而前往英国拒绝让莱布尼兹跟随。1716年离世,享年70岁。
“牛顿不能正确理解微积分,所以没有在《原理》中使用。”(那时的牛顿对充满了数学严谨性、美学优雅和直观特点的古希腊数学给予高度赞扬,并批判地继承了笛卡尔的思想···)

(?抽空要研究一下这图,书上说“原理认为行星的轨道是椭圆;重力与物体间距离平凡反比。”据说钱德拉塞卡有通俗解读)(阿基米德重心法计算抛物线围成的面积···)
牛顿自创“广义二项式”求解三角函数等复杂函数,扩大了积分的应用范围。
17世纪,笛卡尔、帕斯卡、费马、牛顿、莱布尼茨等创造性天才横空出世,天才的世纪。18世纪时英雄的世纪,伯努利家族、欧拉、达朗贝尔、拉格朗日、拉普拉斯等
3
更多微积分的应用
(这是一本很理想的书。想来大学期间少有对知识的力量感,反而中学的时候对古诗词还有点意境的拓宽。
考上好大学目前看知识卷的能力和耐力,和科学的天赋和爱好无大的关系了。)
sinx cosx 微分4次后会变为原样。
e=2.17828···是雅各布·伯努利发现的。
(手把手教你用微积分)
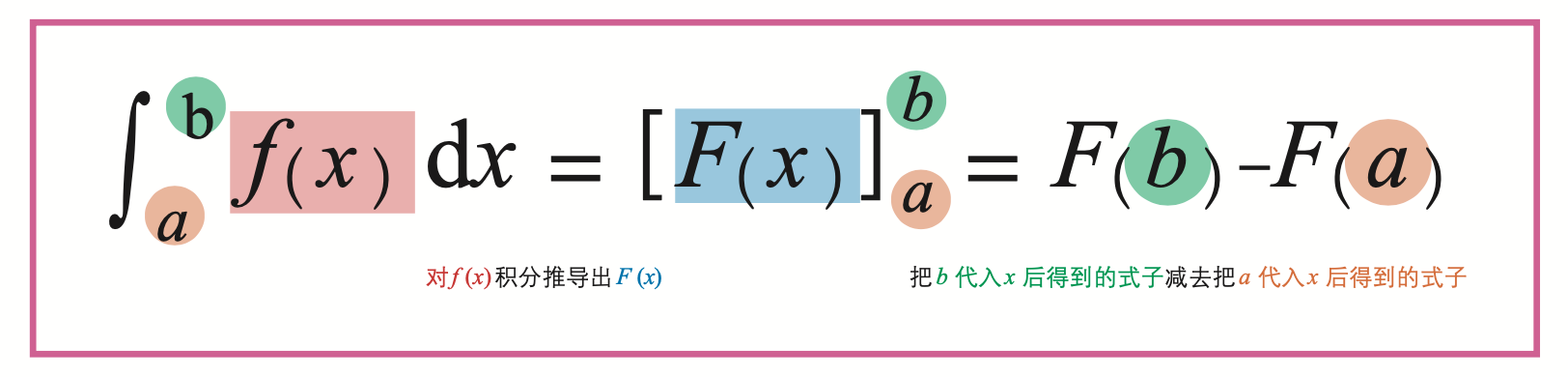
(本书中用微分推导开普勒面积定律,有速度角标有问题。试着修订一下)
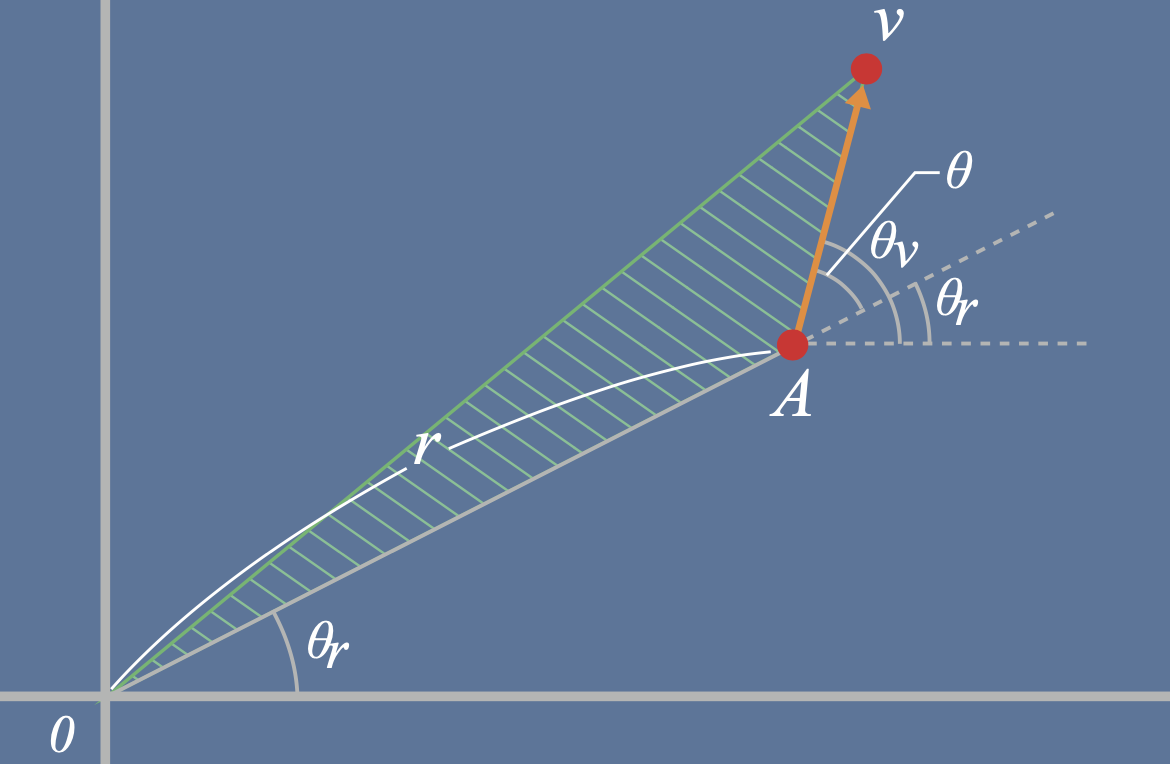



根据“积的微分公式
如果面积速度是一定的,那么关于时间的导数为零。

 ,
, ,
,
 银河系行星不会离开太阳,所以力一定指向太阳方向,以太阳为基准点,行星的面积速度是一定的。(满足角动量守恒)
银河系行星不会离开太阳,所以力一定指向太阳方向,以太阳为基准点,行星的面积速度是一定的。(满足角动量守恒)
(发展部分等有能力又有热情的时候读吧)