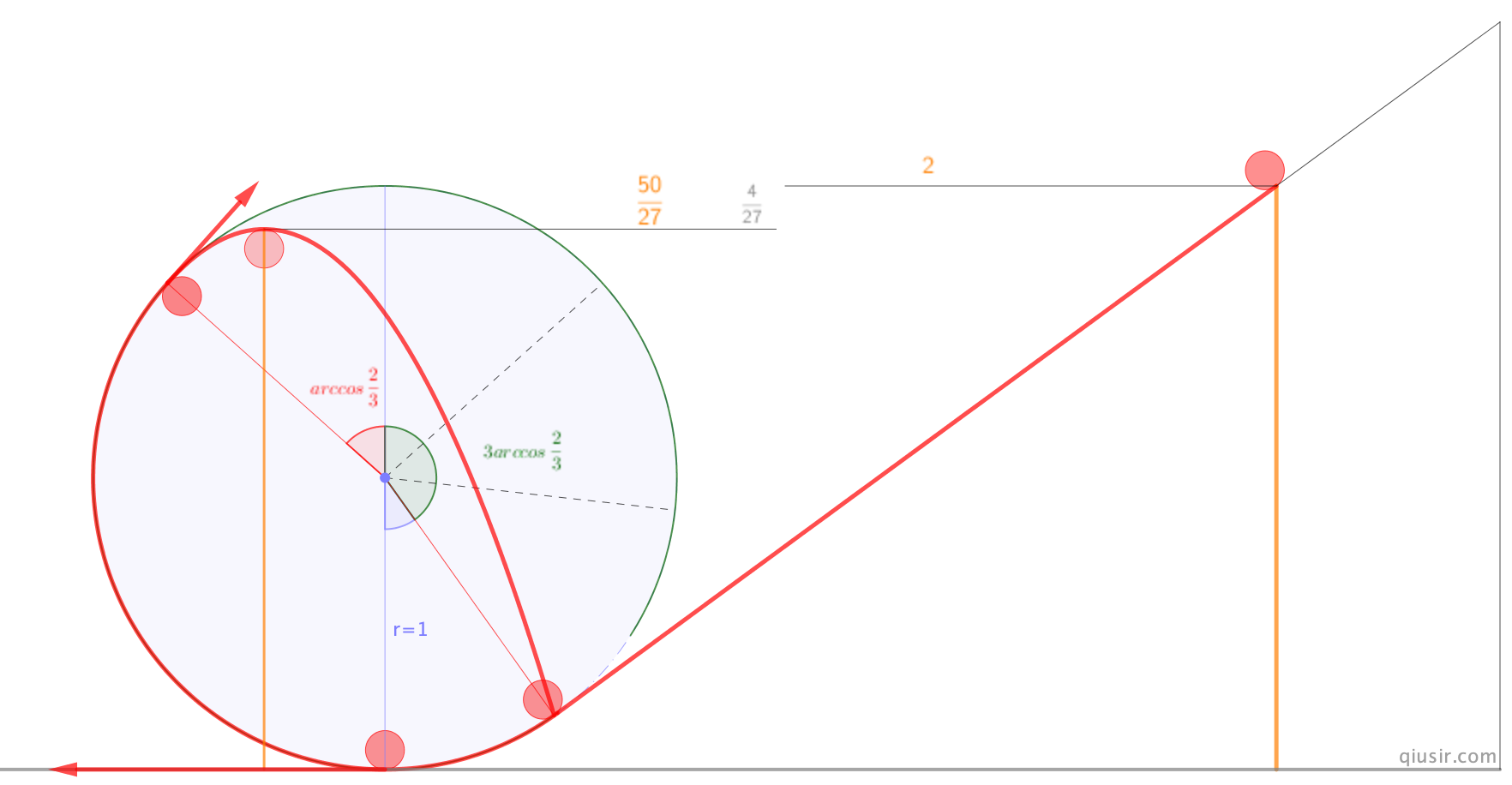
几年前我曾编过一道题目,竖直平面光滑轨道上,求小球从2r等高处静止释放上升的最大高度。起初不少学生不理解为什么不能到达圆形轨道最高点,因为那并不违反能量守恒,后来有学生陆续能计算出$$\frac{5}{3}r$$,最后为数不多的学生能继续计算,斜上抛的运动学角度或者求出抛体最高点动能再用机械能守恒,计算出$$h_{max}=\frac{50}{27}r$$…
前一阵子注意到高三模拟的一道题目和上面很像,但我当时记错了数据,有两位学生(远卓等,他觉得后面的结论很神奇,也期待他们的论证)算出复杂的分数…
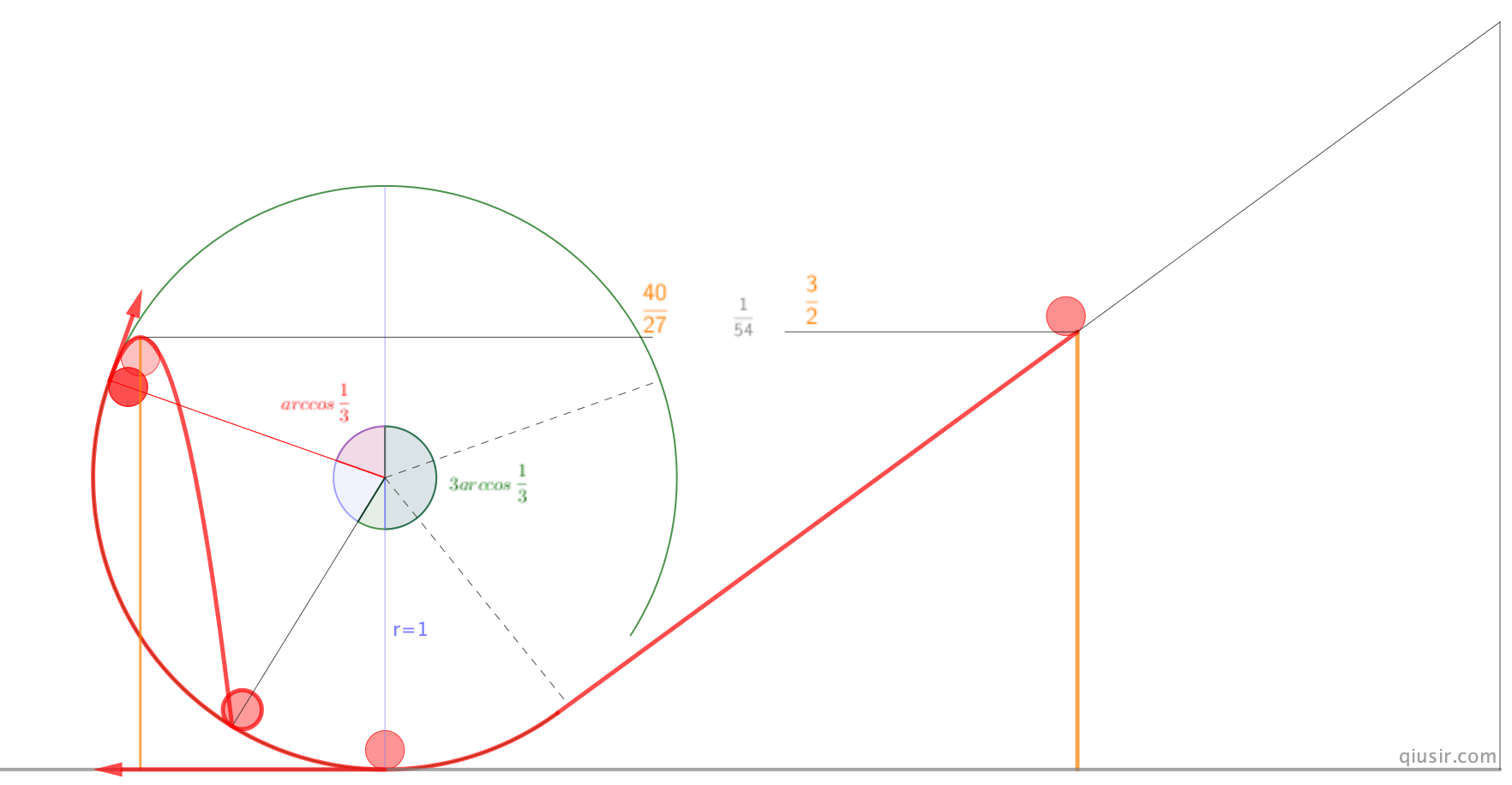
昨天在推上看到@TaRoS_physics分享的结果,以前没有留意到30°(落到水平点最外点)、45°(落到中心对称点)、60°(竖直点)有这么好的结论。就让侯课代表检验一下并找找规律,当然我自己也没有闲着…
关于满足机械能守恒的竖直平面圆周运动的脱离点与落点角度等疑惑,今天用电脑计算了一下,不仅原来结论很完美,似乎还有小的发现,落到圆周上的点是脱离点和竖直面的3倍角,等我要发布的时候发现@hakuryu27071454也给出了一样的结论,我如费赖登塔尔所言的reinvent…