等速圆周的向心力证明

上图是2011年杨振宁先生在香港浸会大学演讲[?]PPT的一张截图，年近九十的他还记得七十多年前自学到向心加速度的事情，作为教师深知对加速度的直觉和向心加速度向量运算结果的冲突是一个普遍的认知现象，正如杨先生提到的那样，对向心加速度求解的理解也是很好的提升机会。

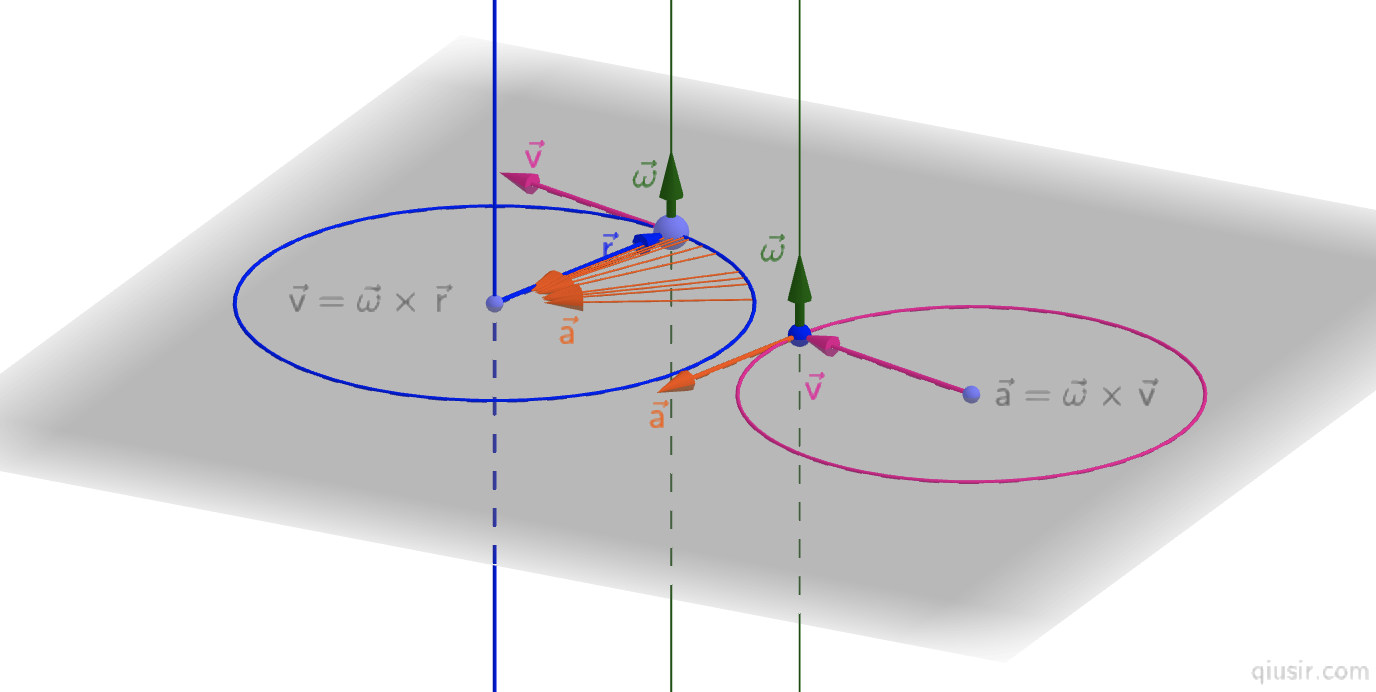
①重新思考这个问题（deriving formula for centripetal acceleration）也是受胡茗淞同学分享的一种旋转类比方法的启发，以匀速转动物体为参考点进行向量平移，向心加速度a、角速度$$\omega$$和线速度v分别和等速圆周运动的线速度v、角速度$$\omega$$和半径r对应，$$v=\frac{\Delta r}{\Delta t}$$，$$a=\frac{\Delta v}{\Delta t}$$，既然$$v=\omega r$$，那$$a=\omega v$$。（$$\vec{a}=\vec{\omega}\times\vec{v}$$是$$\vec{v}=\vec{\omega}\times\vec{r}$$关于时间的求导…）
关于角速度的矢量方向，满足右手螺旋定则，大拇指方向为ω方向，而线速度和向心加速度类比电磁感应部分的手则…

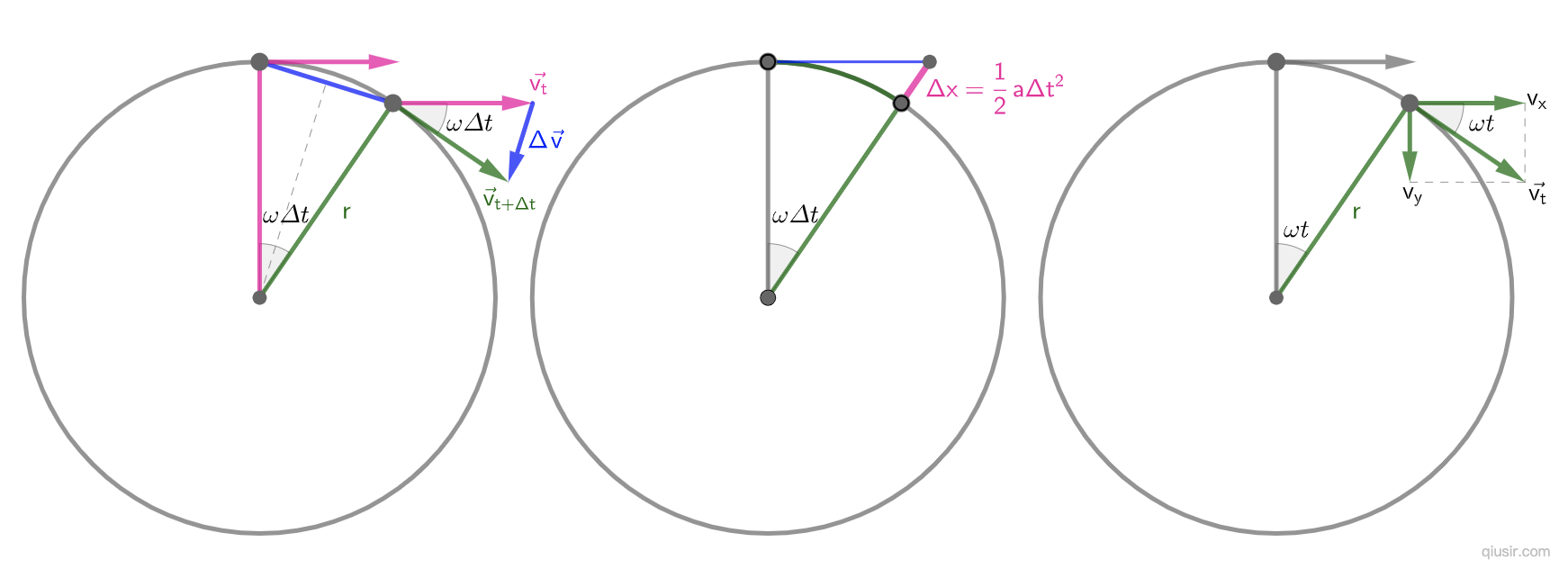
我接触的最常见的方法是矢量三角形和几何三角形相似：
②这离不开用弧长近似弦长。$$\Delta l\approx \Delta s =v \Delta t$$，$$\frac{\Delta v}{\Delta s}=\frac{v}{r}$$，$$\frac{\Delta v}{v\Delta t}=\frac{v}{r}$$，$$a=\frac{\Delta v}{\Delta t}=\frac{v^2}{r}$$；
③或者用弧长$$\Delta s =r\Delta\theta=r\omega\Delta t$$近似弦长，$$\frac{\Delta v}{r\omega\Delta t}=\frac{v}{r}$$，$$a=\frac{\Delta v}{\Delta t}=\omega^2r$$；
④也可以用正弦近似求弦长，$$l=2rsin(\frac{\omega\Delta t}{2})\approx r \omega\Delta t$$；
⑤当然完全可以在矢量三角形中直接求解，$$sin(\frac{\omega \Delta t}{2})=\frac{\frac{1}{2}\Delta v}{v}$$，$$\frac{\Delta v}{\Delta t}=\omega v$$…
⑥在矢量三角形中用余弦定理，
$$\Delta{v}=\sqrt{2v^2-2v^2cos(\omega\Delta t)}=\sqrt{2}v\sqrt{1-cos(\omega\Delta t)}=\sqrt{2}v\sqrt{2sin^2\frac{\omega\Delta t}{2}}=2vsin\frac{\omega\Delta t}{2}$$
$$\Delta v=v\omega\Delta t$$，$$\frac{\Delta v}{\Delta t}=v\omega$$…

和前面不同，另一个思路是从运动叠加的角度推导向心加速度：
⑦这里可以顺便练习一下余弦的近似计算，$$\frac{r}{cos(\omega \Delta t)}-r=\frac{1}{2}a\Delta t^2$$，$$cos(\omega \Delta t)\approx 1-\frac{(\omega \Delta t)^2}{2}$$，$$\frac{1}{2}a\Delta t^2=r\frac{\frac{1}{2}\omega^2\Delta t^2}{1-\frac{1}{2}\omega^2\Delta t^2}$$…
⑧同样是运动叠加，用勾股定理近似计算也可，$$\frac{1}{2}a\Delta t^2=\sqrt{r^2+(v\Delta t)^2}-r$$，简化处理，$$\frac{1}{2}a\Delta t^2=\frac{(\sqrt{r^2+(v\Delta t)^2}-r)(\sqrt{r^2+(v\Delta t)^2}+r)}{\sqrt{r^2+(v\Delta t)^2}+r}=\frac{v^2\Delta t^2}{\sqrt{r^2+(v\Delta t)^2}+r}$$，$$\frac{1}{2}a=\frac{v^2}{2r}$$…
⑨对于上面的处理，孙浚豪同学是用移项后平方，高阶无穷小量消项。$$\frac{1}{2}a\Delta t^2+r=\sqrt{r^2+(v\Delta t)^2}$$，$$ar\Delta t^2+r^2+(\frac{1}{2}a\Delta t^2)^2=r^2+v^2\Delta t^2$$，$$ar=v^2$$

⑩用速度矢量的正交分解可关联到简谐振动，$$v_x=\omega r cos(\omega t)$$，$$v_y=-\omega r sin(\omega t)$$，分别对时间求导得$$a_x=-\omega^2 r sin(\omega t)$$，$$a_y=-\omega^2 r cos(\omega t)$$，$$a=\sqrt{a_x^2+a_y^2}$$，和通常的极限法分析$$\Delta v$$向心不同，这里可以直接得出加速度方向指向圆心的结论。

重新整理了这些对应试的意义不大，除了顺便用一下物理中偶尔用到的近似计算，大多数学生只关心结论就可以应付了，但对知识认知的层次是不同的。通常的中学物理教学，不仅对积分和导数的应用过分延后，对向量（矢量）的运算更是脱节，而且意识上的重视明显不够。

美国科学促进会(AAAS)1985年启动2061计划（哈雷彗星2061年会再次光临地球），帮助美国人提高科学、数学及技术素养，“美国历史上最显著的科学教育改革之一”
，号称“终极的科学计划”
。“既然数学对理解自然科学等具有中心重要地位，因而我们再次强调需要把数学与这些学科以综合的方式去教。综合的方法表明，一个现象的数学描述具有阐明和加强的效果。”

直接用加速度是位置矢量关于时间的二阶导数运算不香吗？有时更一般的方法反而会降低认知难度。
$$sin\theta=\frac{y}{r}$$，$$cos\theta=\frac{x}{r}$$
$$\vec{v}=vsin\theta \hat{x}-vcos\theta \hat{y}=v\frac{y}{r}\hat{x}-v\frac{x}{r}\hat{y}$$
$$\vec{a}=\frac{d\vec{v}}{dt}$$，$$\vec{a}=\frac{v}{r}(v_y\hat{x}-v_x\hat{y})$$
$$\left|\vec{a}\right|=\frac{v}{r}\sqrt{v_x^2+v_y^2}=\frac{v^2}{r}$$
更一般：
$$\vec{r}(t)=rcos\theta(t)\hat{x}+rsin\theta(t)\hat{y}$$
$$\vec{v}=\frac{d\vec{r}}{dt}=r(-sin\theta(t))\frac{d\theta}{dt}\hat{x}+rcos\theta(t)\frac{d\theta}{dt}\hat{y}$$
对于等速圆周运动，$$\frac{d\theta}{dt}=\omega=const.$$
$$\vec{v}=\omega r(-sin\theta(t))\hat{x}+rcos\theta(t)\hat{y}$$
$$\vec{a}=\frac{d\vec{v}}{dt}=-\omega^2 r(cos\theta(t))\hat{x}+sin\theta(t)\hat{y}$$
$$\left|\vec{a}\right|=\omega^2 r$$
前面是对向心加速度的推导，而对它的理解大多局限在直接应用的层面，在FloatHeadPhysics频道上看到更直观的逻辑：
半径不变速度加倍，相同两个位置的速度变化量同样加倍，而所需要时间则因为速度加倍而减半，所以速度变化量应该是平方倍；同理，速度不变半径加倍，相同位置（角度）的速度变化量不变，而由于弧长加倍速度不变，所需时间加倍，那速度变化率减半。

特地找到杨振宁演讲的原视频截取了关于向心加速度的一段。因为战乱等原因，数学教授的儿子也没有学过高中物理，但似乎不妨碍他日后在物理学上的贡献。而现在的小朋友似乎学的有点多…

1937年杨振宁的父亲到西南联大教书，一家人搬到昆明。1938年高二的杨振宁参加大学入学考试（同等学力报考），报考化学系也要求考物理，没有学过高中物理的他借了一本高中物理学在家自学了一个月，觉得物理学很有意思，比化学还有意思，一考入西南联大立刻从化学系转到物理系。

另，
发现有用$$F_g$$表示重力的，我觉得这样非常方便，和$$F_f$$、$$F_n$$等表示一致，比用W表示更统一，特别是和万有引力常数G区分开。至于向心加速度，$$a_n$$、$$a_c$$都可以，我更习惯弹力用$$F_N$$，而向心力用$$F_n$$，都是normal…
关于是匀速圆周运动还是等速圆周运动，个人更偏向台湾那等速圆周运动的称谓…