几年前我曾编过一道题目，竖直平面光滑轨道上，求小球从2r等高处静止释放上升的最大高度。起初不少学生不理解为什么不能到达圆形轨道最高点，因为那并不违反能量守恒，后来有学生陆续能计算出$\frac{5}{3}r$，最后为数不多的学生能继续计算，斜上抛的运动学角度或者求出抛体最高点动能再用机械能守恒，计算出$h_{max}=\frac{50}{27}r$...
前一阵子注意到高三模拟的一道题目和上面很像，但我当时记错了数据，有两位学生（远卓等，他觉得后面的结论很神奇，也期待他们的论证）算出复杂的分数...

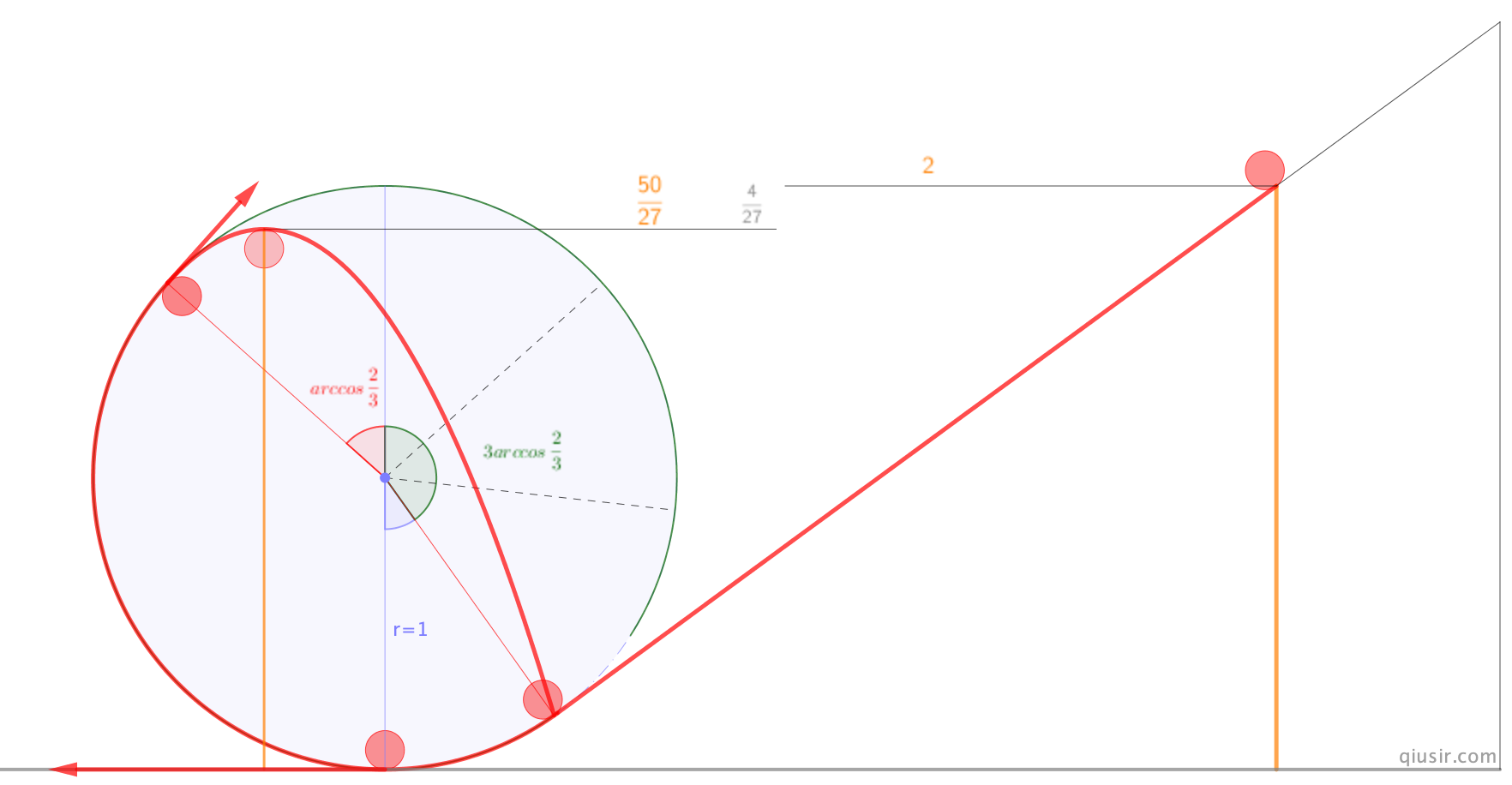
昨天在推上看到@TaRoS_physics分享的结果，以前没有留意到30°（落到水平点最外点）、45°（落到中心对称点）、60°（竖直点）有这么好的结论。就让侯课代表检验一下并找找规律，当然我自己也没有闲着...
关于满足机械能守恒的竖直平面圆周运动的脱离点与落点角度等疑惑，今天用电脑计算了一下，不仅原来结论很完美，似乎还有小的发现，落到圆周上的点是脱离点和竖直面的3倍角，等我要发布的时候发现@hakuryu27071454也给出了一样的结论，我如费赖登塔尔所言的reinvent...




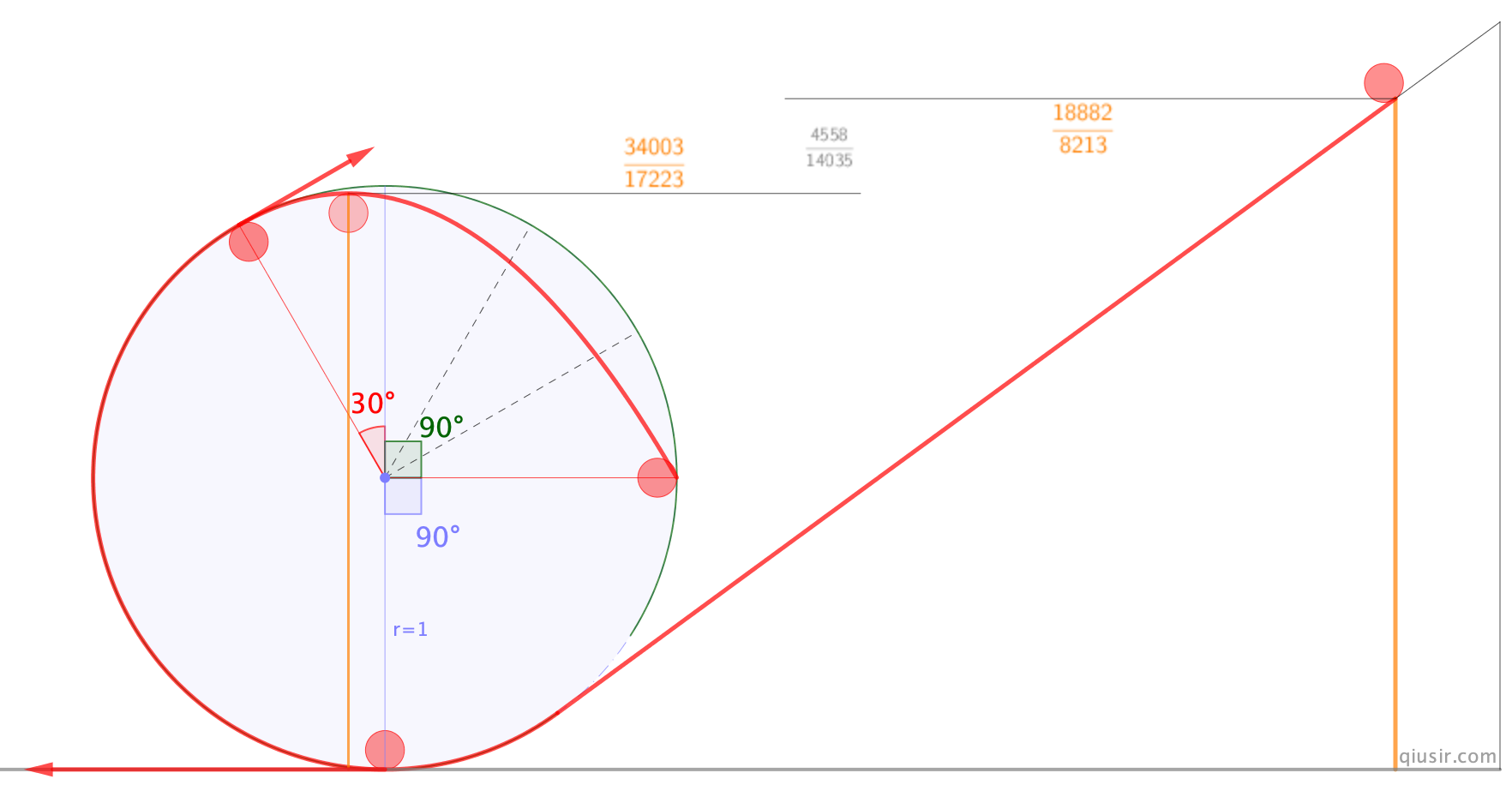
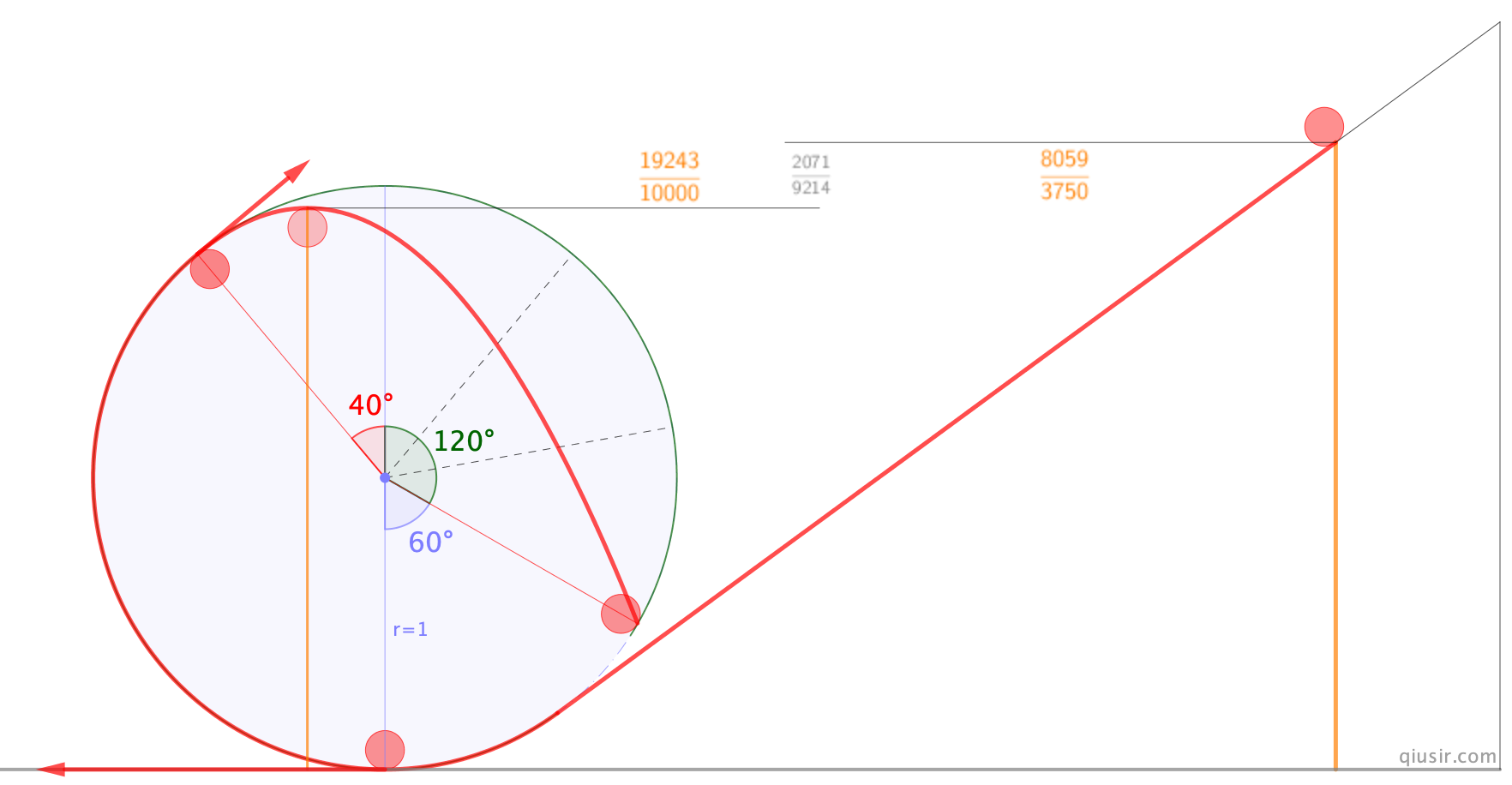
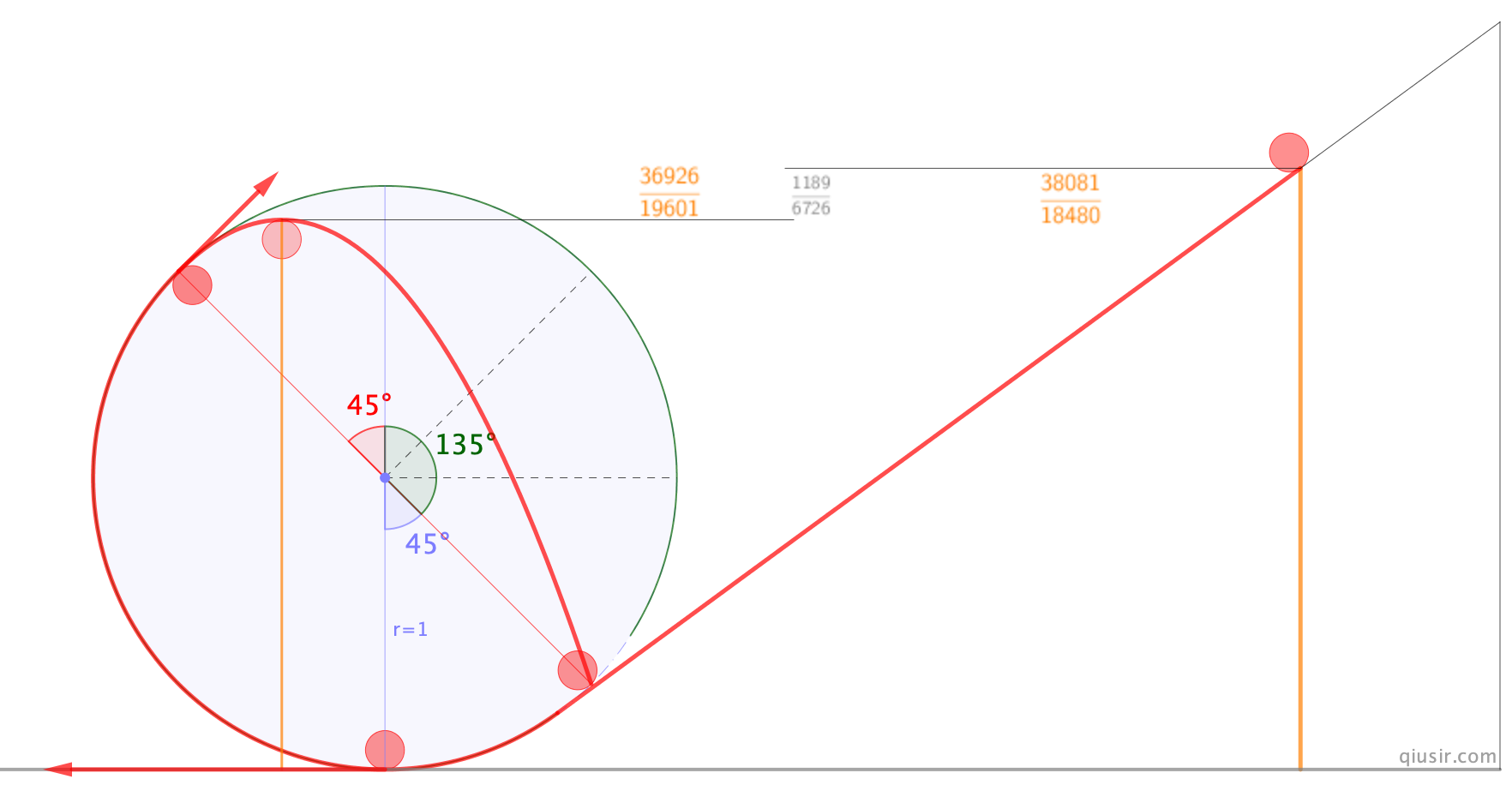
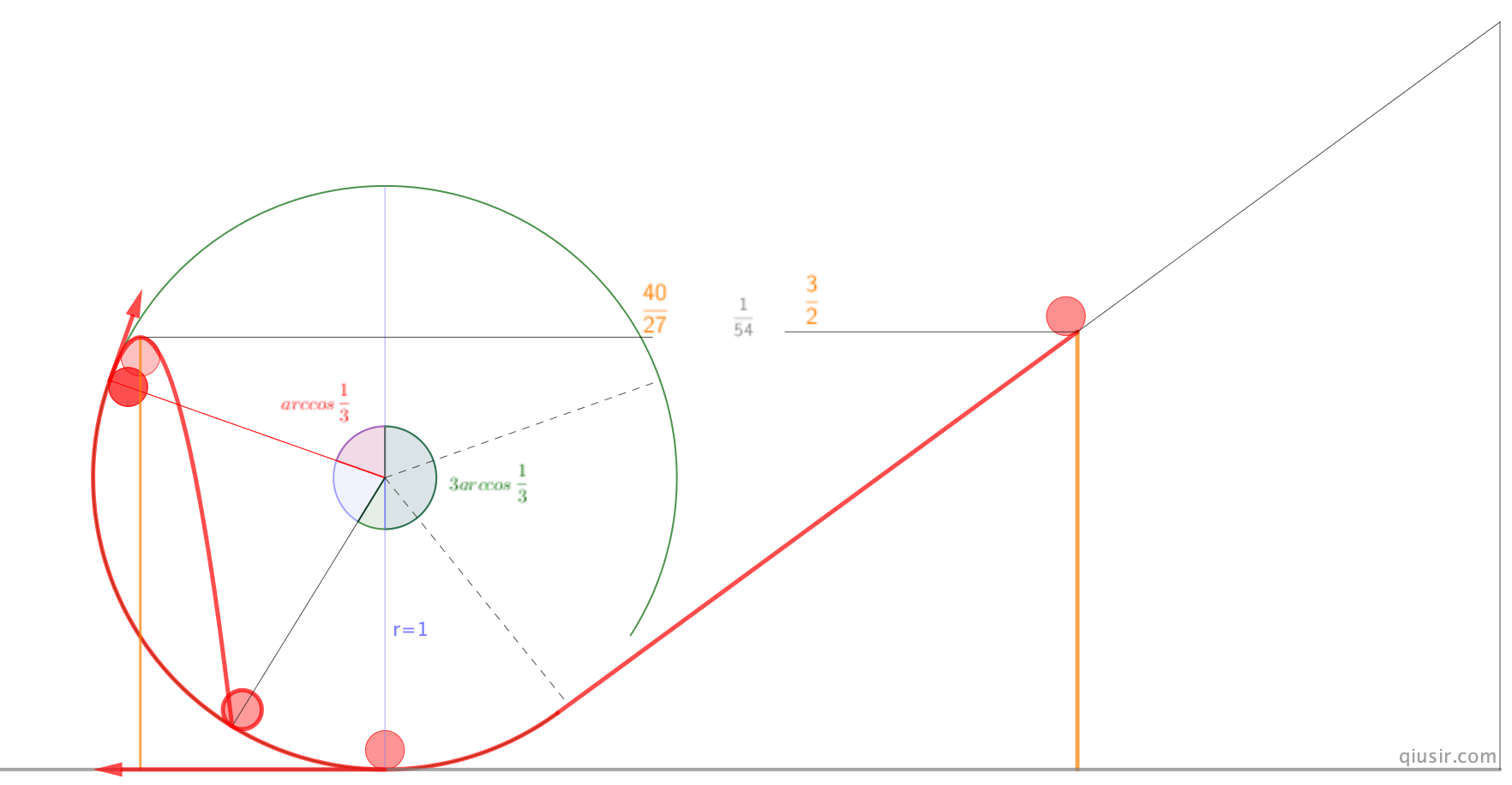
如果从编题练手的角度，从$\frac{7}{4}r$高度释放的小球数据较好，一方面最大的高度是$\frac{27}{16}r$，另一方面小球是从与竖直60°角处分离，并恰能落回最低点...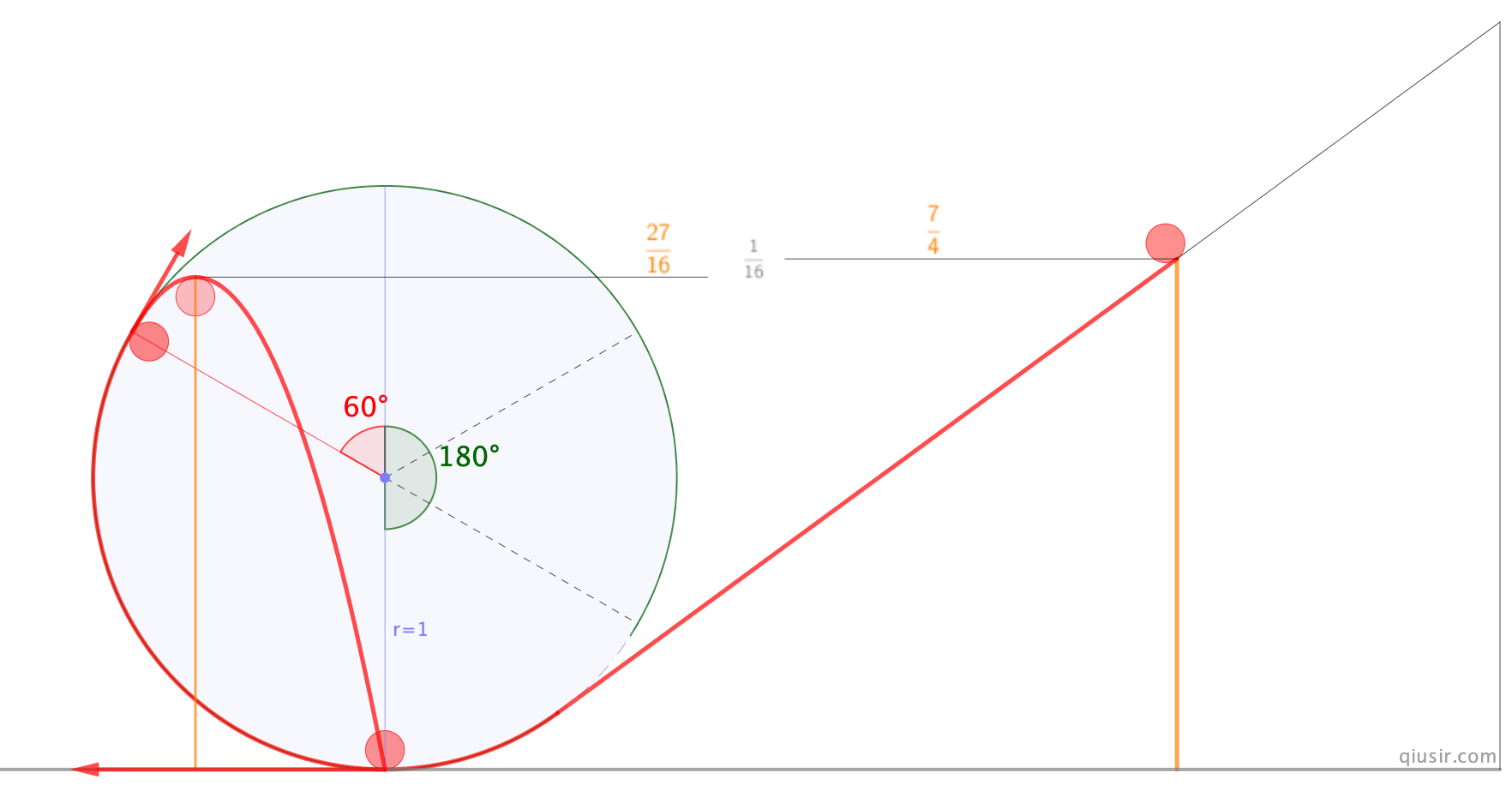

update:
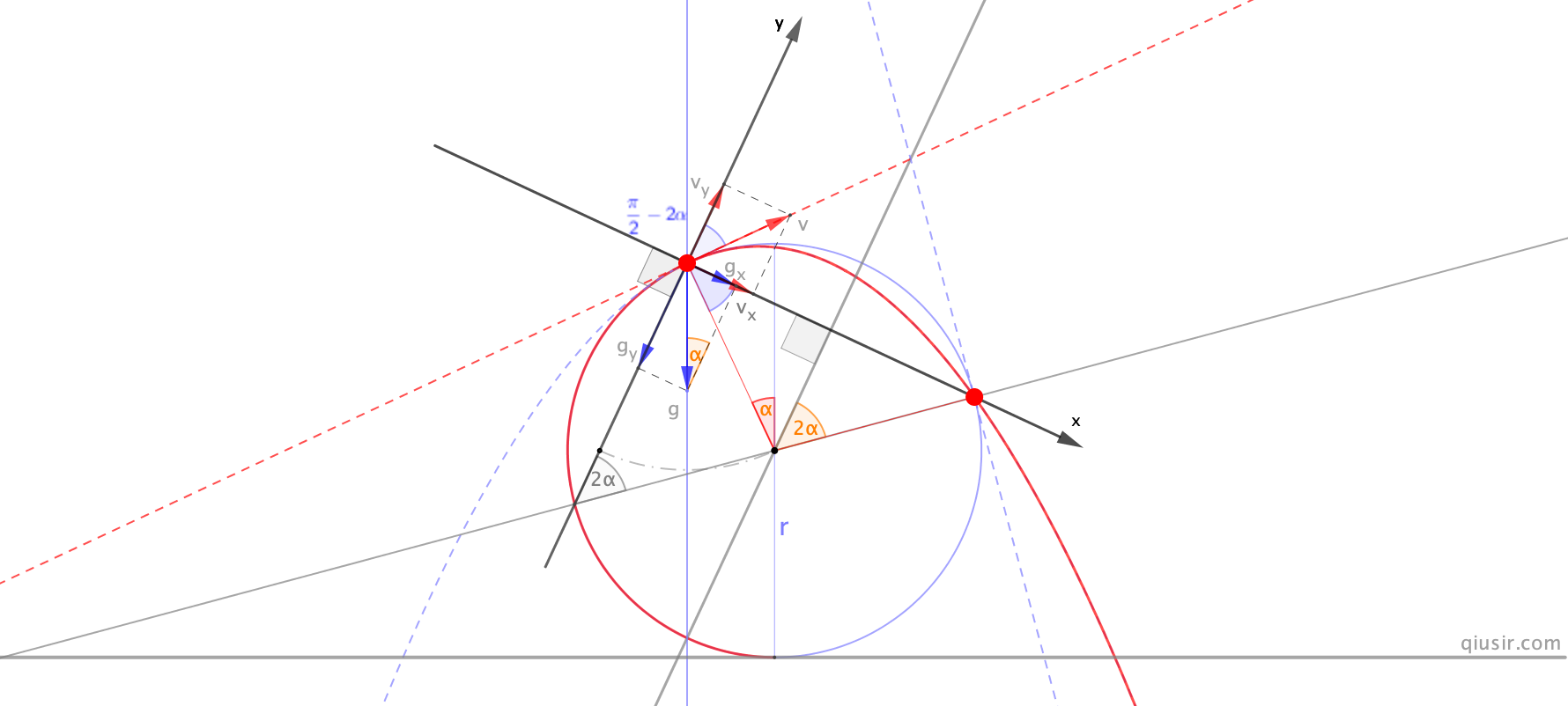
关于这个问题的证明，一种是通过解析的方法（也留意到@YS55749378的耐心证明，估计明天我学生中能有好的结果），我当然倾向物理的思路，不仅是证明，更试图找到更通俗的解释。先是把三倍角还原成四倍再转化为两倍角的对称，然后建立新的坐标系并对速度和加速度分解...
$v_x=vsin(\frac{\pi}{2}-2\alpha)$，$g_x=gsin\alpha$
$v_y=vcos(\frac{\pi}{2}-2\alpha)$，$g_y=gcos\alpha$
$t=2\frac{v_y}{g_y}=\frac{4vsin\alpha}{g}$
$x=v_xt+\frac{1}{2}g_xt^2$
另，根据分离条件，即重力法向分力提供向心力，$mgcos\alpha=m\frac{v^2}{r}$
代入，$x=4rsin\alpha cos\alpha(cos(2\alpha)+2sin^2\alpha)$得出$d_x=2rsin(2\alpha)$...

很遗憾并没有发现预料的简洁结论。如果不从四倍角度看，也可以通过作出圆心关于分离点竖直方向对称点和分离点连线的垂直方向的直线和圆周交点即是落点位置；或圆心关于分离点竖直方向对称点与分离点连线和圆的交点与圆心连线的直径上的另一点即为落点...下面算是更好的简化。

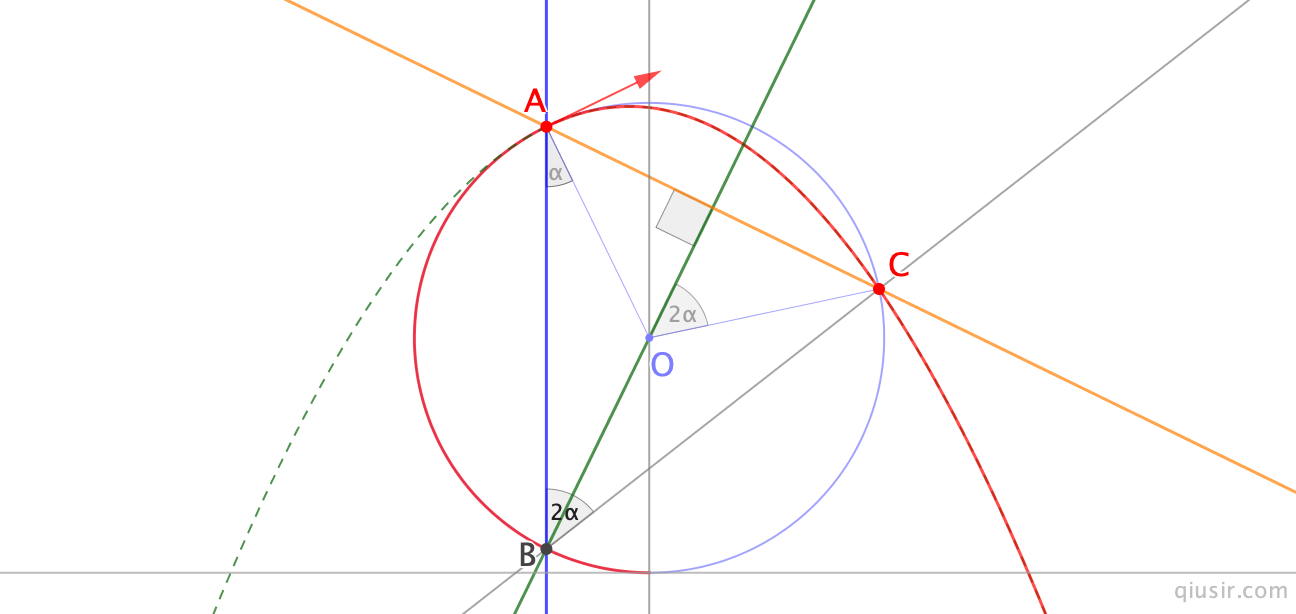
当然，如果单纯几何构造的角度看也算简单：
1、构造过分离点A的竖直直线，也是重力方向，与圆相交B点；2、连接B与圆心的直线；3、过分离点A做垂线，与圆相交C即为落点。也是A关于直线的对称点。

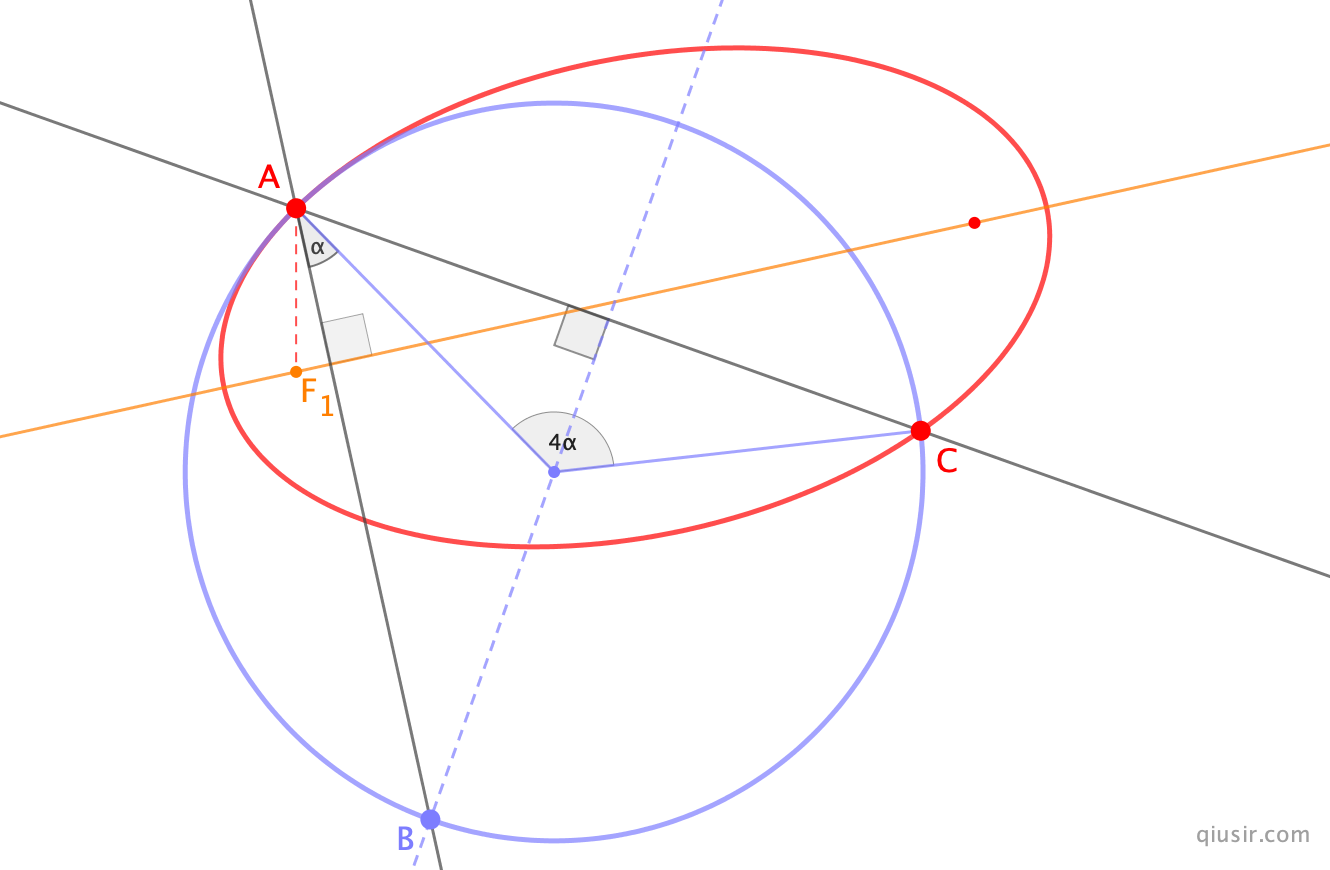
还是感觉有比上面的论证更简洁的见解，也检验了一下，上述结论也是抛物线曲率圆（密切圆，Osculating circle）的一般性质（之前竟然没有注意原来的圆形轨道不过是原本抛物线的密切圆而已）。那椭圆和双曲线呢，估计原本的竖直方向会变成指向引力中心的方向？原来这是个普适的结论：过分离点与圆锥曲线对称轴的平行或垂线和密切圆相交，然后分离点与连接交点和密切圆圆心（曲率中心）的垂线与密切圆的交点即是回归点。（也是分离点和回归点与密切圆圆心夹角还是4α）

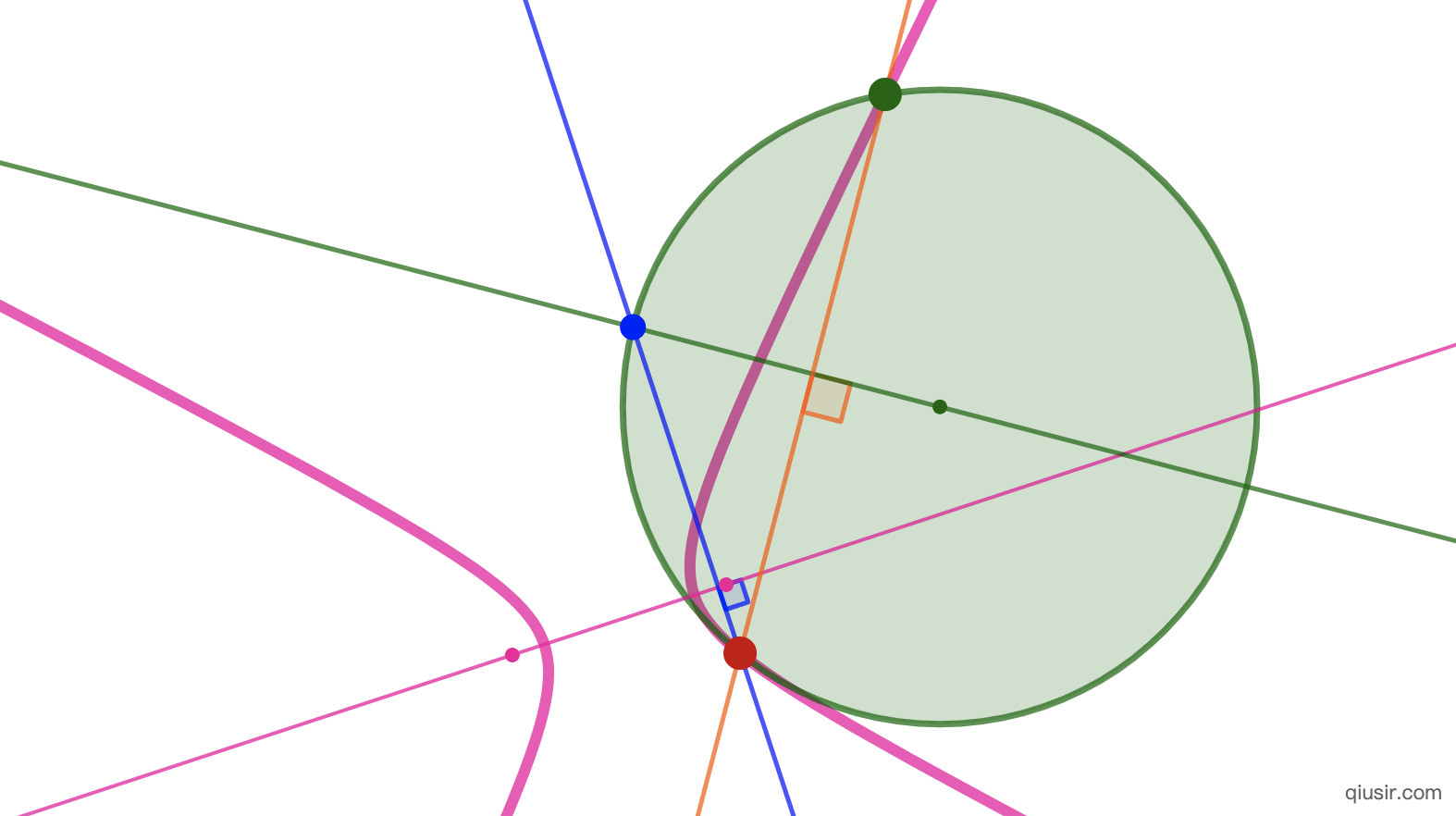
附高一七班王远卓的证明：

附（物理和数学上并不困难的问题，学生主动想到更一般的探索的愿望和努力值得留名）
晨西设定释放点距离圆形轨道圆心高度h，则脱离点与竖直夹角$cos\theta=\frac{2h}{3r}$，如此设定结果简洁；浩睿设定释放点距离地面高度为半径n倍，则上升最大高度为$n-\frac{4}{27}(n-1)^3$...

On this day..

• 徐晨语の蝴蝶定理学习笔记 - 2024
• 求师得数位学习2016寒假总结 - 2016
• 高速公路 - 2008
• 学习只是生活的一个部分 - 2007
• 抢跑 - 2006
• 要有点精神 - 2005
• 空间交费办理完毕 - 2004
• 教师是袜子也是脚 - 2004