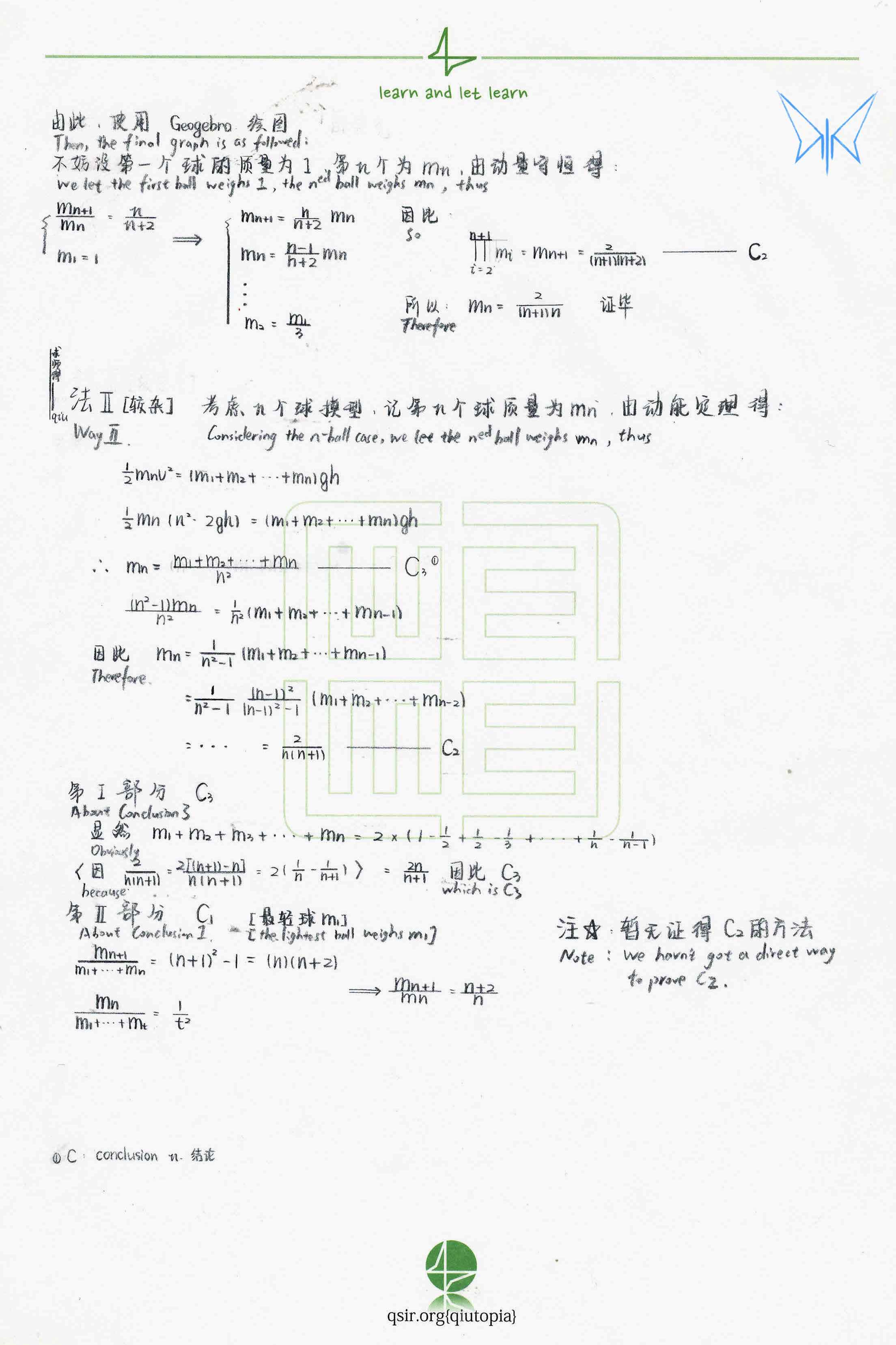
试着用gemini的学习辅导来学习
麦克斯韦（James Clerk Maxwell）是一位非常了不起的科学家，物理学家们常把他与牛顿和爱因斯坦并列。麦克斯韦最伟大的贡献把电和磁彻底“统一”在了一起。这组方程是以麦克斯韦命名的，但将它们提炼为现代教科书里那种简洁、对称的4个矢量方程形式的人，主要是英国物理学家、工程师亥维赛（Oliver Heaviside）
一、麦克斯韦方程组（积分形式）
1、高斯静电定律（有电荷的地方就有电场线“喷”出来或“吸”进去。）
$\oint_S \mathbf{E} \cdot d\mathbf{A} = \frac{Q}{\varepsilon_0}$
2、高斯磁定律（磁场线总是闭合的，没有起点也没有终点。这也意味着世界上不存在磁单极子。）
$\oint_S \mathbf{B} \cdot d\mathbf{A} = 0$
3、法拉第电磁感应定律（那个负号代表产生的电场总是试图阻止磁场的变化。）
$\oint_L \mathbf{E} \cdot d\mathbf{l} = -\frac{d\Phi_B}{dt}$
4、安培-麦克斯韦定律（磁场可以由两种方式产生：一是电流I，二是变化的电场。这是麦克斯韦最伟大的补充，正是这一项预言了电磁波的存在。）
$\oint_L \mathbf{B} \cdot d\mathbf{l} = \mu_0 I + \mu_0 \varepsilon_0 \frac{d\Phi_E}{dt}$
这四个方程就像是一场双人舞：变化的磁场产生电场，变化的电场又产生磁场。它们互为因果，循环往复。

二、麦克斯韦方程组的微分形式，两个核心概念：散度（Divergence）和旋度（Curl）。它们不再描述整个区域，而是描述空间中每一个点上的电磁场是如何变化的。我们可以把这四个方程看作是电磁场的“局部基因图谱”：
1、电场的散度（高斯定律）（描述电荷如何产生电场）
$\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}$
$\nabla \cdot \$（读作del dot）散度衡量的是向量场从一个点“发散”出来的程度。
电荷密度ρ是电场的源头。正电荷就像喷泉（散度为正），负电荷就像漏斗（散度为负）。
2、磁场的散度（高斯磁定律）（描述磁单极子不存在）
$\nabla \cdot \mathbf{B} = 0$
磁场的散度永远为0，这意味着磁场没有起点也没有终点，磁场线总是闭合的。
散度（Divergence）：想象水管里的水。如果一个地方有喷头在喷水，那里的散度就是正的，这一点就像是一个“源头”（Source）；如果有排水口，散度就是负的，这一点就是一个“汇”（Sink）。
$\nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}$，向量场F偏导数的运算。
一个向量场通过闭合曲面的通量等于该曲面所包围体积内的散度的体积积分。$\oint_S \mathbf{F} \cdot d\mathbf{S} = \int_V (\nabla \cdot \mathbf{F}) \, dV$

3、电场的旋度（法拉第定律）（描述变化的磁场如何产生旋转的电场）
$\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}$
$\nabla \times$（读作 del cross）是旋度，它衡量的是向量场在一个点附近“打转”的程度。
变化的磁场（磁场对时间的导数）会在周围感生出一个旋转的电场。
4、磁场的旋度（安培-麦克斯韦定律）（描述电流和变化的电场如何产生旋转的磁场）
$\nabla \times \mathbf{B} = \mu_0 \left( \mathbf{J} + \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t} \right)$
磁场的“旋涡”有两个来源：一是电流密度，二是变化的电场。
旋度（Curl）：想象水面上有一个小木片。如果水流让小木片原地转圈，说明那里的水流旋度不为 0。
$\nabla \times \mathbf{F} = \left( \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z} \right) \mathbf{i} + \left( \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x} \right) \mathbf{j} + \left( \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \right) \mathbf{k}$
旋度和斯托克斯定理（Stokes' Theorem）密切相关，后者表示曲线围成的闭合环路上某向量场的线积分等于该曲面上的旋度的曲面积分
$\oint_C \mathbf{F} \cdot d\mathbf{l} = \iint_S (\nabla \times \mathbf{F}) \cdot d\mathbf{S}$
我们已经讨论了散度（源头）和旋度（旋转），你觉得如果一个向量场的散度和旋度在空间中每一处都被确定了，这个场是不是就被唯一确定了呢？（这涉及到一个著名的物理定理——亥姆霍兹定理）。
三、张量形式
$\partial_\mu F^{\mu\nu} = \mu_0 J^\nu$
张量形式的麦克斯韦方程组是更为一般的表达方式，通常用于相对论框架下。
洛伦兹力方程:$\frac{d\mathbf{p}}{dt}=q\left(\mathbf{E}+\mathbf{v}\times\mathbf{B}\right)$
虽然不完全是麦克斯韦方程的一部分，但洛伦兹力方程描述了电磁场对带电粒子的作用。
四、范例
1、均匀带电球体、球壳、无限长带电导线和无限大带电平面的电场，利用对称性，选取高斯面，球面、圆柱面、药丸盒
ChatGPT对于环形电流中心处磁场，竟用“安培定理”（安培环形定理）给出一堆的顾左右而言它的解释，让它出图示，竟然也给出看着很正确的东西，当然，当你发现问题后，它会告诉你用比奥-萨伐尔定律···

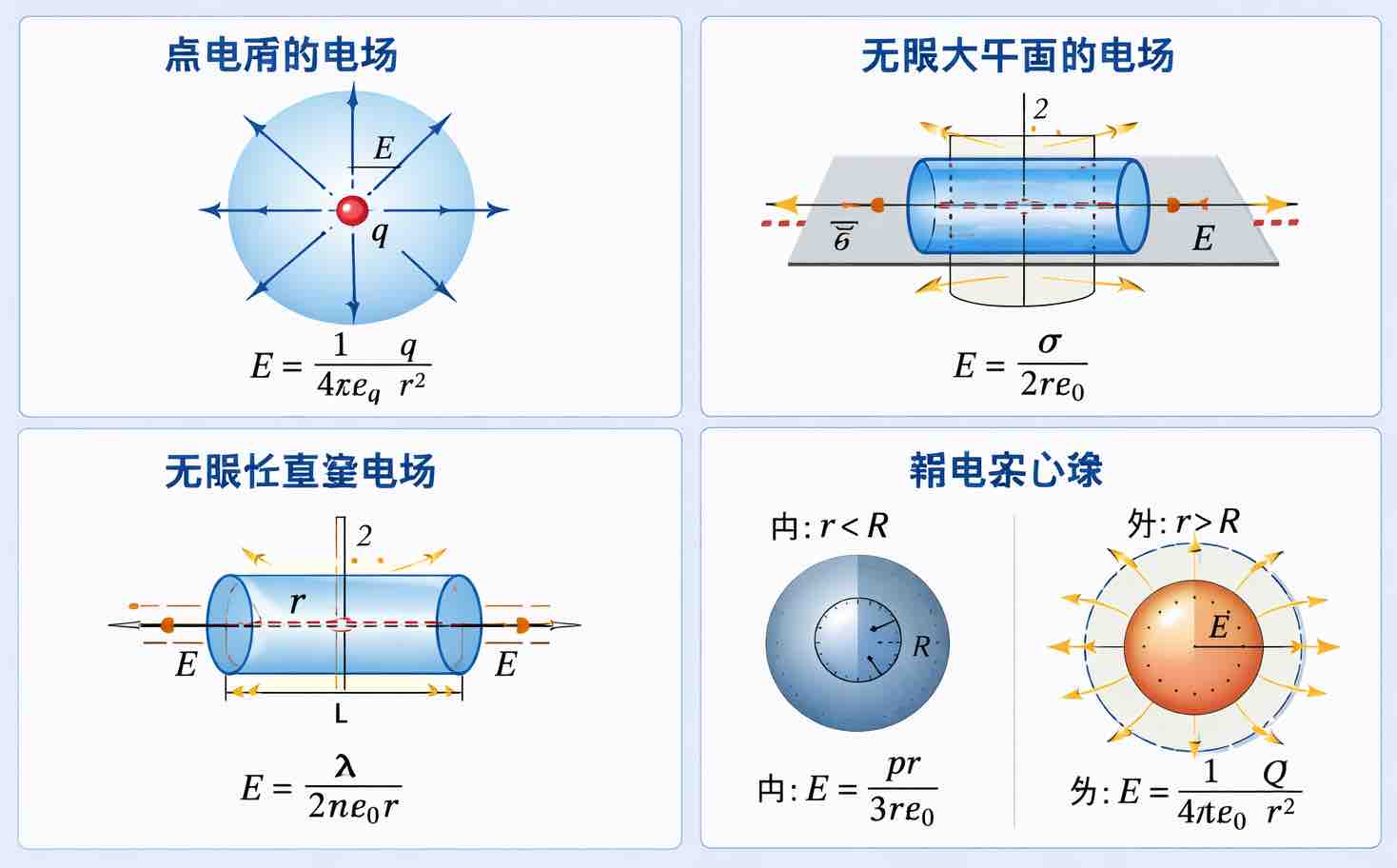
很正确的样子
2、推导光速
在没有任何电荷和电流的真空中，麦克斯韦方程组表现出高度的对称性：
$\nabla \cdot \mathbf{E} = 0$
$\nabla \cdot \mathbf{B} = 0$
$\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}$
$\nabla \times \mathbf{B} = \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}$
对法拉第定律取旋度
$\nabla \times (\nabla \times \mathbf{E}) = \nabla \times \left( -\frac{\partial \mathbf{B}}{\partial t} \right)$
使用矢量恒等式展开左边
$\nabla(\nabla \cdot \mathbf{E}) - \nabla^2 \mathbf{E} = -\frac{\partial}{\partial t} (\nabla \times \mathbf{B})$
代入真空条件和安培-麦克斯韦定律
$-\nabla^2 \mathbf{E} = -\frac{\partial}{\partial t} \left( \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} \right)$
得到电场波动方程
$\nabla^2 \mathbf{E} = \mu_0 \epsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2}$
类比经典物理中波动方程通式$\nabla^2 f = \frac{1}{v^2} \frac{\partial^2 f}{\partial t^2}$
结合推导结果得出光速$c = \frac{1}{\sqrt{\mu_0 \epsilon_0}}$
五、注释
1.$\nabla$(Del/Nabla)是一个算子，通常被称为Nabla算子，是一组操作指令。像一个“多功能工具刀”，在三维空间中指向函数变化最快的方向。用于计算梯度（Gradient）、散度（Divergence）和旋度（Curl）。
2.$\Delta$(Delta)是一个预定义的变化量，通常代表“差值”。
在微积分中，它也代表拉普拉斯算子，$\Delta=\nabla^2$，用来衡量一个场在某一点与其周围平均值的差异。

AI画图，让我想起求师得最初的slogan，a Question a Chance!不是不是应该改成A Question An Apple

同学知道我不怎么参加集体活动，关于看话剧，这几天非正式提过几次，串场过程中课代表小鹿童鞋穿着戏服跑回来邀请，再不去说不过去啊，特地让肖老师陪我去。手机比较旧，早早没电了，还好，两个班都拍到了。

10班：威尼斯商人





10班剧组

4班：红岩

JQX/进取芯 席明纳第22期（2025.12.09）

从麦克斯韦方程组到光速

JQX|Xiao

一、波动方程
对于一个机械波，想描述它在空间的分布，它的方程为：$D(x) = A \sin \frac{2\pi}{\lambda} x$。如果这个机械波以速度 $v$ 向右传播，则 $t$ 时刻的波函数为：$D(x,t) = A \sin \left[ \frac{2\pi}{\lambda} (x - vt) \right]$，引入周期 $T$ 可变形为：$D(x,t) = A \sin \left( \frac{2\pi x}{\lambda} - \frac{2\pi t}{T} \right)$。
简化为：$D(x,t) = A \sin (kx - \omega t)$
其中 $k = \frac{2\pi}{\lambda}$，称为波数。由此得到波的传播速度为：$v = \lambda f = \left( \frac{2\pi}{k} \right) \left( \frac{\omega}{2\pi} \right) = \frac{\omega}{k}$
二、麦克斯韦方程组
麦克斯韦方程组包含以下四个方程：
1. $\oint \vec{E} \cdot d\vec{A} = \frac{Q}{\epsilon_0}$
2. $\oint \vec{B} \cdot d\vec{A} = 0$
3. $\oint \vec{E} \cdot d\vec{l} = - \frac{d\Phi_B}{dt}$
4. $\oint \vec{B} \cdot d\vec{l} = \mu_0 I + \mu_0 \epsilon_0 \frac{d\Phi_E}{dt}$
其中第一个是电场的高斯定律，第二个公式说明了磁场无源，第三个是法拉第电磁感应方程，第四个是一般形式的安培环路定律。前面三个我们都比较熟悉，下面我们对第四个方程进行一下解释：
安培环路定律的一般形式为：$\oint \vec{B} \cdot d\vec{l} = \mu_0 I$。但是科学家们发现了这样的矛盾：假设有一个平行板电容器连着两根导线，正在充电。我们对其中一根导线取一个高斯环路，可以求出它的磁场环路积分。但是现在的问题是等式右面的电流 $I$ 应该怎么选择？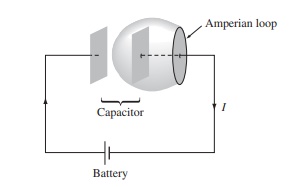
我们认为电流是指“通过环路所围成的截面”的电流。但是这个截面我们可以任意选择：比如我们可以选择一个平面使这个导线穿过它；或者选取一个曲面，**就像吹起的泡泡糖**，让它把电容器的一个极板包含进去。这样我们发现一个问题：选的第二个曲面（泡泡糖）并没有电流穿过它，但是我们明明选取的高斯环路没有变，也就是说虽然没有电流，但是等式右边一定有什么东西**替代**了这个电流。我们把这个电流叫做**位移电流**。
根据高斯定律：$\Phi_E = E \cdot A = \frac{Q}{\epsilon_0}$，我们对它求导可以得到：$\frac{d\Phi_E}{dt} = \frac{1}{\epsilon_0} \frac{dQ}{dt} = \frac{1}{\epsilon_0} I$。
得到电流大小：$I_d = \epsilon_0 \frac{d\Phi_E}{dt}$，我们称这个电流大小为位移电流，它反应了电场的变化会产生磁场。空间中的磁场可以由两部分产生，一部分由电流产生，一部分由变化的电场产生。当空间中既有电流，又有变化的电场，就是如下的表述形式：$\oint \vec{B} \cdot d\vec{l} = \mu_0 (I + I_d) = \mu_0 I + \mu_0 \epsilon_0 \frac{d\Phi_E}{dt}$
三、麦克斯韦方程组推导光速
1. 麦克斯韦方程组（真空环境）。先考虑真空中没有电荷 ($Q=0$) 和电流 ($I=0$)。这时麦克斯韦方程组的积分形式如下：
1. 电场高斯定律：$\oint \vec{E} \cdot d\vec{A} = 0$
2. 磁场高斯定律：$\oint \vec{B} \cdot d\vec{A} = 0$
3. 法拉第电磁感应定律：$\oint \vec{E} \cdot d\vec{l} = - \frac{d\Phi_B}{dt}$
4. 安培-麦克斯韦定律：$\oint \vec{B} \cdot d\vec{l} = \mu_0 \epsilon_0 \frac{d\Phi_E}{dt}$
2. 建立一阶偏微分关系：假设电磁波沿 $x$ 轴传播，电场 $E$ 沿 $y$ 轴，磁场 $B$ 沿 $z$ 轴，即 $E = E_y = E_0 \sin(kx - \omega t)$ 和 $B = B_z = B_0 \sin(kx - \omega t)$。
利用法拉第定律计算电场等式左右两边，可得：$\frac{\partial E}{\partial x} = - \frac{\partial B}{\partial t}$ —— (式 1)
利用安培-麦克斯韦定律（选取 $xz$ 平面回路）：
计算磁场环路积分与电通量变化率（位移电流），可得：$- \frac{\partial B}{\partial x} = \mu_0 \epsilon_0 \frac{\partial E}{\partial t}$ —— (式 2)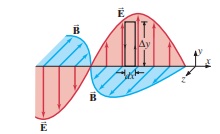
3. 代入波动方程
计算电场和磁场对空间 $x$ 和时间 $t$ 的偏导数：
$\frac{\partial E}{\partial x} = k E_0 \cos(kx - \omega t)$ 且 $\frac{\partial E}{\partial t} = -\omega E_0 \cos(kx - \omega t)$
$\frac{\partial B}{\partial x} = k B_0 \cos(kx - \omega t)$ 且 $\frac{\partial B}{\partial t} = -\omega B_0 \cos(kx - \omega t)$
4. 比较系数
代入法拉第定律关系式：
由 $\frac{\partial E}{\partial x} = - \frac{\partial B}{\partial t}$，代入可得：$k E_0 \cos(\dots) = - [-\omega B_0 \cos(\dots)]$。化简得：$k E_0 = \omega B_0$，整理得到：$\frac{E_0}{B_0} = \frac{\omega}{k} = v$
由 $- \frac{\partial B}{\partial x} = \mu_0 \epsilon_0 \frac{\partial E}{\partial t}$，代入安培定律关系式可得：$- k B_0 \cos(\dots) = \mu_0 \epsilon_0 [-\omega E_0 \cos(\dots)]$。化简得：$k B_0 = \mu_0 \epsilon_0 \omega E_0$，整理得：$\frac{E_0}{B_0} = \frac{k}{\mu_0 \epsilon_0 \omega}$
联立求解：$v = \frac{k}{\mu_0 \epsilon_0 \omega} = \frac{1}{\mu_0 \epsilon_0 (\omega/k)} = \frac{1}{\mu_0 \epsilon_0 v}$即：$v^2 = \frac{1}{\mu_0 \epsilon_0}$
解得：$v = \frac{1}{\sqrt{\mu_0 \epsilon_0}} = c \approx 3.00 \times 10^8 \text{ m/s}$(c=299792458m/s)