教辅|〖教育技术〗

三 03

纵波的疏部密部

最初只是关注到“纵波的疏部密部对应横波的平衡位置”的结论，后来Y老师问及日本教科书上一道纵波疏部密部具体对应的题目，再后来发现很旧一本物理参考书（王沛清编）上有讨论。最近有空就构造了下动态的情况...

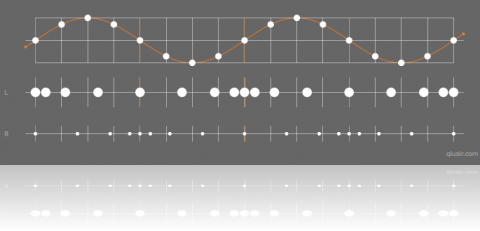
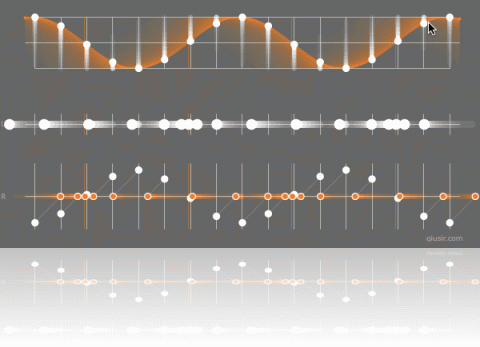
图中正弦曲线是对应纵波的位移位置的图像，下面对应纵波分别是左右为正方向...

如果电脑没有安装GSP，可以通过点击图片观看GIF动画~
关于这个话题，龙TG同学提到用导数的思路甚好，导数大对应的相邻位置的位移差大，对应密部或疏部；导数小，相邻位置的位移差小，对应的非疏密...
GSP-纵波的疏部密部 (5679)
更新了董ZnCu童鞋用投影的一种思路...
发现Mac的LICEcap上小巧实用~

w的多种求解，关联单摆...

十一 11

Small Teacher Big Data

教辅|〖教育技术〗评论关闭

大多的演讲都是脱稿，随性利于即时发挥，也容易吸引听众，却很乏耐心去细致整理，也只能记忆些只言片语，多少也是个念想不是。

上午来学校先是连上三节高三的课，期间还有新疆的于老师听课。稍做调整，收拾下资料去辽中，没过中午已经在辽中路边拍稻田了。这是神马的节奏哈~

为了减少麻烦就自己开车去，导航提醒我一会铁西区一会于洪区，反正我看路标北京方向就好。这个季节看地里收割完的水稻一朵朵的很有感，交流旅游一体了哈~

提前到了，顺便刷下车，这差价抵过高速通行费了呢~
暑假在辽宁大厦的一次会上，茨榆坨中学徐校长（图片是学校刘副校长）就邀请去和老师们做个交流，本学期高三，一直是各种忙碌，今日成行。

茨榆坨中学的环境不错。校长引用我的微言开场。说有一百六十多教师，按名入座。Small Teacher Big Data~挑了几张...

说是信息技术为主的交流，期间不乏一些我对教育的理解~有的Keynote有提过，就不重复发图片了（这一年做过几次交流，面向对象虽然不同，但重叠的部分还是不少）。

从随手拍、大小微博、动态数理到教育思考...

见有学生桌布上写到，“你就像一朵花，喜欢是把你折断，爱是尽心呵护你盛开。”刚看了还真有点惭愧，可转念想，在老师的眼里，“你更像一棵树，喜欢是在某一侧面的驻足，爱是悉心修护。”为人师长不能以爱之名摧残，但爱也不是袖手旁观...

一个多小时的交流气氛融洽，少有摆弄手机的，偶有拍拍照的。

从生命存在的角度看，每个人都是不平凡的，反倒我们从事的工作很平凡。那对平凡的尊重源自于自我的尊重，当你被忽视时不应恼火，反倒要有深深的同情。另，你看到的很多不平凡不是他生命本身于你的优越，更多不过是处境的不同，这更像是一种机缘，也如物理的势能，但它是机械能的一部分。

(图片中NEYC取自校友设计的文化衫，很荣幸”邱叔叔“在C上~)
初以为求学乃求师；后以为求学乃求知；现在想来求学乃求己，而所谓知识不过是知己识己。这样看来，求师得不过是引导学生成为自己的一个初始阶段，最终的目标还是要帮助学生知己识己，让学生自求自得。

虽说是个镇的中学，但硬件条件已经很好了，和衡中有一比了~可以想象来年开春这教学楼前的美景。

无功无名，一介小书生何谈讲学，但交流是很好的学习方式。校方定义为学习交流很是恰当。

平日的课堂上会和学生交代，多年以后，你或许还会发现老师的一些观点是不恰当，甚至是错误的。但大家不要忘记，多年前那个讲台前和你们分享自己想法的小老师的真诚。其实这话也适用于今天，只是你们不要忘记的是那个真实的老学生。

晚餐就客气了。回城可谓轻车熟路~
录像资料还没到，感兴趣可以参阅Lectures[?]的演讲列表。

三 20

耶路撒冷弦桥

教研|〖数理探究〗, 教辅|〖教育技术〗 7 Comments »

不经意看到善科网上的这篇文章（桥梁、弦艺术和Bézier曲线[?]，英语原文[?]），除了被耶路撒冷弦桥（erusalem Chords Bridge）的艺术特质所感染，同样被缆线的纵横所吸引，对桥弦包络（缆线边缘的轮廓）的曲线好奇...

把这样一件复杂的实体抽象出一个平面的模型，我最先想到的是以前多次构造过的定长杆滑动的范例[?]，一度以为那包络线和文章里提到的同属。一方面数学班张潇勇等同学（程同学和鲜同学同样有参与）给出了代数式，非抛物线，另一方面通过抛物线的光学特性反正，才意识到这是非常不同的两个模型...

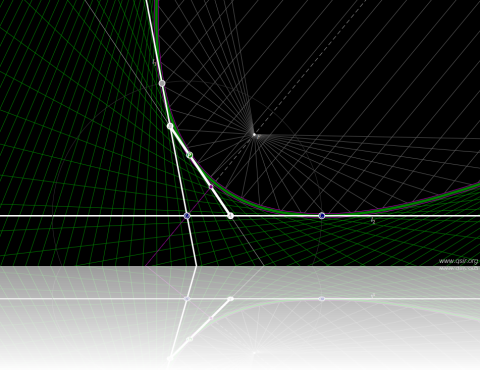
构造从相互垂直的两直线上的点到交点距离和相等开始，中间尝试了多种方法，又把线段的包络拓展到直线的包络，后来发现要实现完整的抛物线包络，需要加入距离差为常数，再后来借助点的坐标值引入了比例，再把直线拓展到任意夹角，在用同样的比例在线段上缩放（考虑多阶贝塞尔曲线构制）...

O为两直线的交点、CO为定长、AO+BO=CO/AO-BO=CO\P分线段AB的比例同A分线段OC的比例，也同线段AB上另一点分BA的比例...

一些很表象的结论：包络线是抛物线；角平分线是对称轴；抛物线与两直线的切点在以和与差定值为半径的圆周上；以同样的比例在线段上两个端点分别为中心缩放的点，轨迹要么是抛物线上的点，要么是抛物线对称轴上的点...

立体到平面本就失去很多信息，次模型也没有考虑到力学等因素，甚至没有给出计算和证明，但这不妨碍我们从另一层面探究和发现：

比如椭圆和双曲线是平面上到两定点距离和与距离差为定值的曲线（以前讨论过距离平方和与差的题目），那上述的模型无非是两相交直线上风别两点与交点的距离和与差相等的曲线，而很有趣的是，原来的定长杆在墙角滑动的模型即等棍模型无非是直线上到交点距离平方和为定值，那么自然会想到距离积距离商为常数，如果直线变成圆弧...

也发现经常使用的keynote上图形绘制工具提供的竟然是贝塞尔曲线[?]，而借用同比例回归到定长杆模型中，也会有不少新的认识...

☆直线上到交点距离和&差定值点的连线包络ChordsBridge~ (5347)

三 12