一 16

16-1.机械振动

教学|〖基础物理〗 qiusir 2000

11.机械振动
1、简谐振动
弹簧振子、单摆，竖直放置的弹簧，万有引力下的
2、简谐振动的描述
相位的概念phase
简谐振动的位移描述：所处位置到平衡位置的有向线段。
对应三角函数
平衡位置的特点。
3、简谐振动的回复力和能量
简谐振动的对称性在计算题中常常有应用。
三角函数的导数对应的速度，位移和加速度的关系图像。

一个周期内一个质点运动的路程4A，半个周期2A，其他则需要通过三角函数运算得到。
4、单摆
物体下落，单摆，斜面运动时间的比较。
近似简谐振动的证明。
摆线要求尽量细，伸缩性小，摆球要尽量质量大，体积小的。

5、外力作用下的振动
共振过程中，频率接近的可不一定是周期接近的，相等的除外。

上课带领学生推双星的公式，\frac{L^3}{T^2}=\frac{G(m_1+m_2)}{4\pi^2}，类比开普勒第三定律很容易记忆...而对地球贴地卫星周期公式化简，\frac{R^3}{T_1^2}=\frac{GM}{4\pi^2}，T_1=2\pi \sqrt{\frac{R^3}{GM}}，T_1=2\pi \sqrt{\frac{R}{g}}
类比单摆的公式，T=2\pi \sqrt{\frac{l}{g}}，以及圆锥摆的周期公式T=2\pi \sqrt{\frac{lcos\theta}{g}}，很容易建立起关联。巧妙的是T=2\pi \sqrt{\frac{R}{g}}也是地球上摆长无限的单摆周期，这个时间还是穿越地心隧道（简谐振动）时间的二倍。

‎

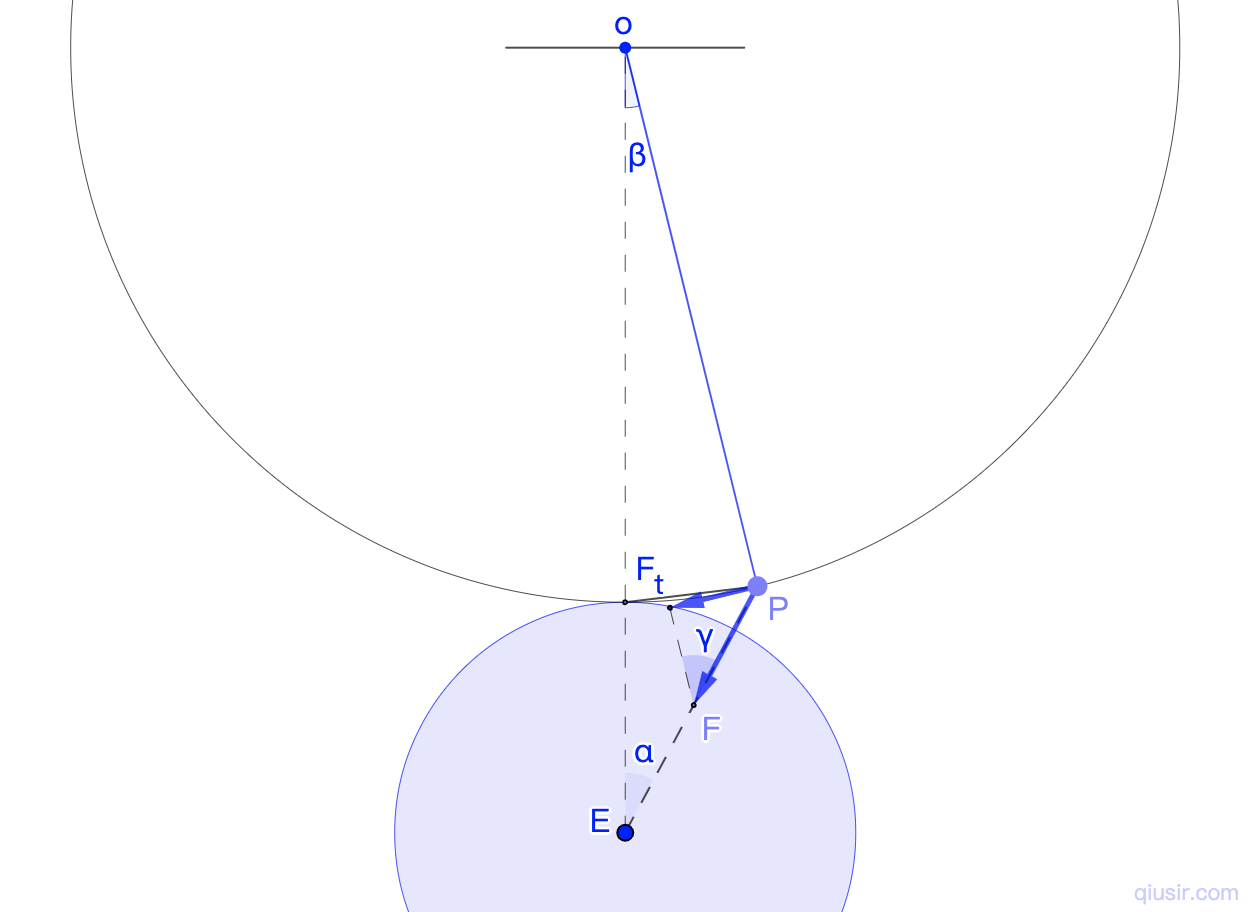
和简谐振动一章推到单摆的周期很接近，设想地面上（可以设想是在很高建筑上）悬点o悬挂摆长l的单摆（摆角很小，一样能近似简振的），万有引力的切向分力提供回复力。
摆球在地表，所有有\frac{GMm}{R^2}=mg，F_t=mgsin(\alpha+\beta)，利用小角度sin\theta\approx\theta，F_t=mg(\alpha+\beta)，因为小角度，位移大小近似弧长也近似水平...F_t=-mg(\frac{1}{R}+\frac{1}{l})x
套用弹簧振子周期公式，T=2\pi\sqrt{\frac{m}{k}}，得T=2\pi\sqrt{\frac{Rl}{g(R+l)}}
带入特殊值到上述公式，比如摆长远小于地球半径，T=2\pi \sqrt{\frac{l}{g}}(l=1m,T约2s)；比如摆长为地球半径，T=2\pi \sqrt{\frac{R}{2g}}（1h）；比如摆长远大于地球半径，T=2\pi \sqrt{\frac{R}{g}}(1.4h)...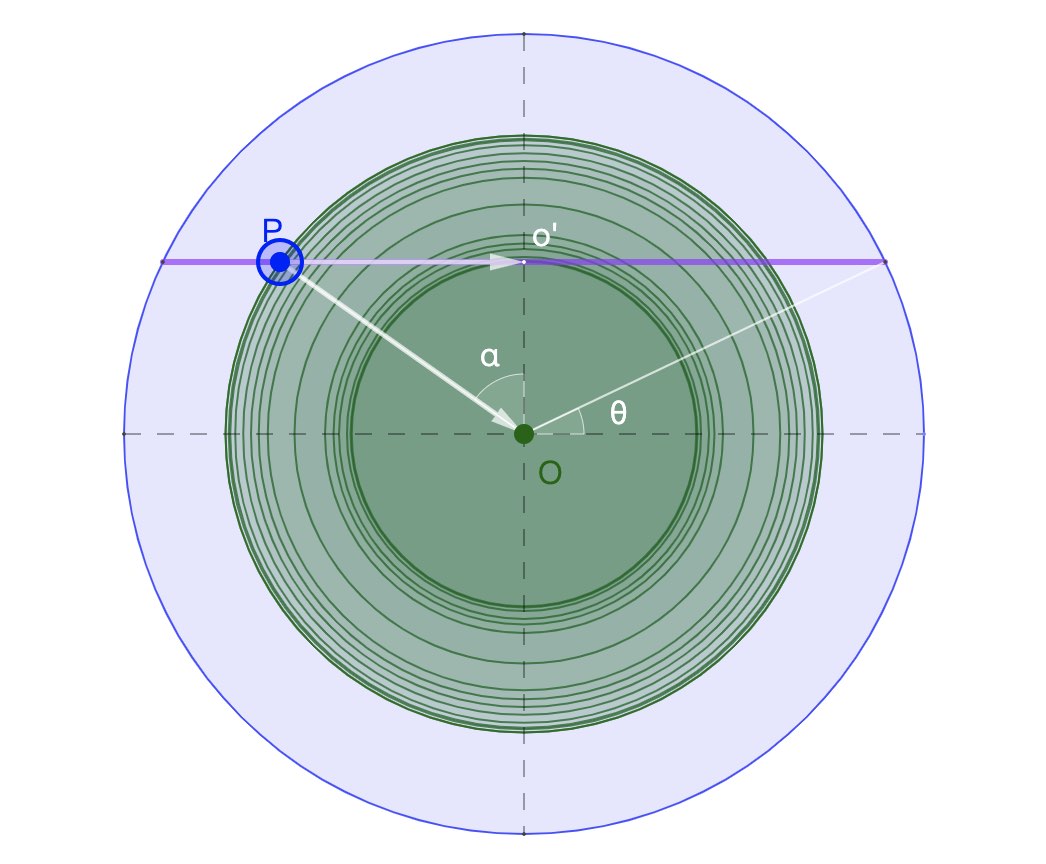
‎

关于贯穿地球的地下铁通行时间的推算，也是用简谐振动的周期。由于球壳对球壳内物体的万有引力为零，所以物体穿行地球时所受的万有引力仅与此处内部球体有关，F=\frac{GMm}{r^2}=\frac{Gm\rho\frac{4}{3}\pi r^3}{r^2}，F_x=-Gm\rho\frac{4}{3}\pi rsin\alpha=-kx...
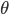继续套用弹簧振子周期公式，T=2\pi\sqrt{\frac{m}{k}}，且gR^2=GM=G\rho\frac{4}{3}\pi R^3，化简后，G\rho\frac{4}{3}\pi=\frac{g}{R}，得T=2\pi \sqrt{\frac{R}{g}}，且与\theta无关。
如果是横贯地心的地下铁，不仅时间和贴地卫星周期相同，更是大撒心心相映的狗粮（圆周运动的投影点）...
当然，这个周期也是和地球半径（大小）无关的，由Kepler's Law III，T=\sqrt{\frac{3\pi}{G\rho}}。地球的平均密度大概是水的5.5倍，对于更高密度的星体，这个运行周期要小得多，如果是中子星内部的隧道...

·我们要变更好/单摆[?]

On this day..

2 Responses to “16-1.机械振动”

  1. mpo Says:
    7月 11th, 2008 at 10:47

    振动图像对应的时刻用三角函数解决，特别注意w的量纲问题，w=2pi/T=2pai*n

  2. qiusir Says:
    10月 31st, 2024 at 11:16

    最近的高三复习，动量之后是机械振动和机械波了。
    北京似乎也是这样，至少八中是。