the Lagrange points

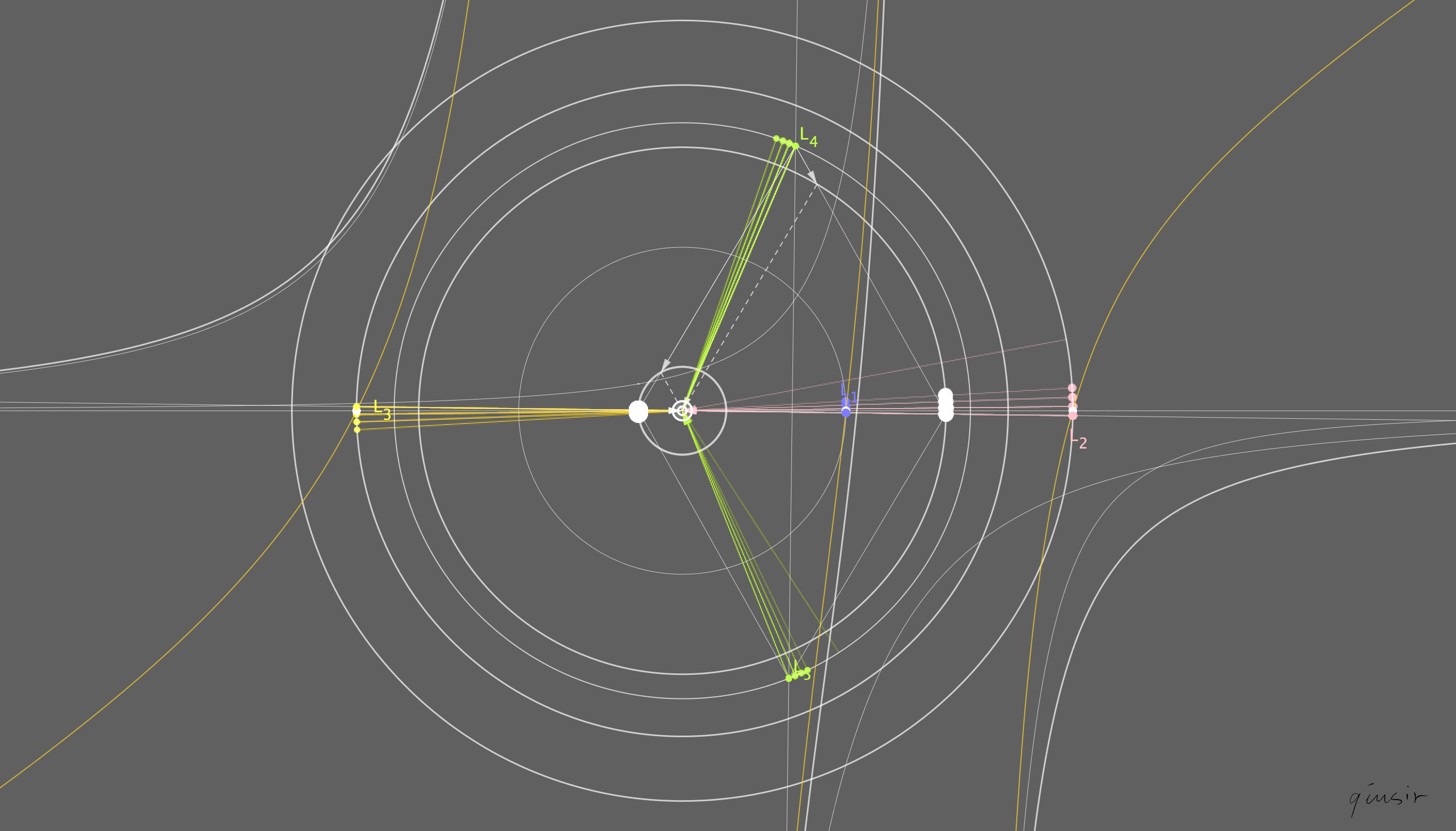
（和MingsongHu一起重新构造了拉格朗日点s）
在了解拉格朗日点之前，应该先对双星系统有所知晓。为了方便，把双星系统中大质量的称为恒星，质量$$M_1$$，比如太阳；小质量的称为行星，质量$$M_2$$，比如地球。
由$$\frac{GM_1M_2}{R^2}=M_1\omega ^2 R_1$$，$$\frac{GM_1M_2}{R^2}=M_2\omega ^2 R_2$$，
得$$\frac{R_1}{R_2}=\frac{M_2}{M_1}$$，$$\omega^2=\frac{G(M_1+M_2)}{R^3}$$
双星以相同角速度围绕质心（到旋转中心距离与质量反比）旋转，角速度由质量和距离决定。

在双星系统中引入第三个天体，为同前面统一，这里称卫星，由于$$m<

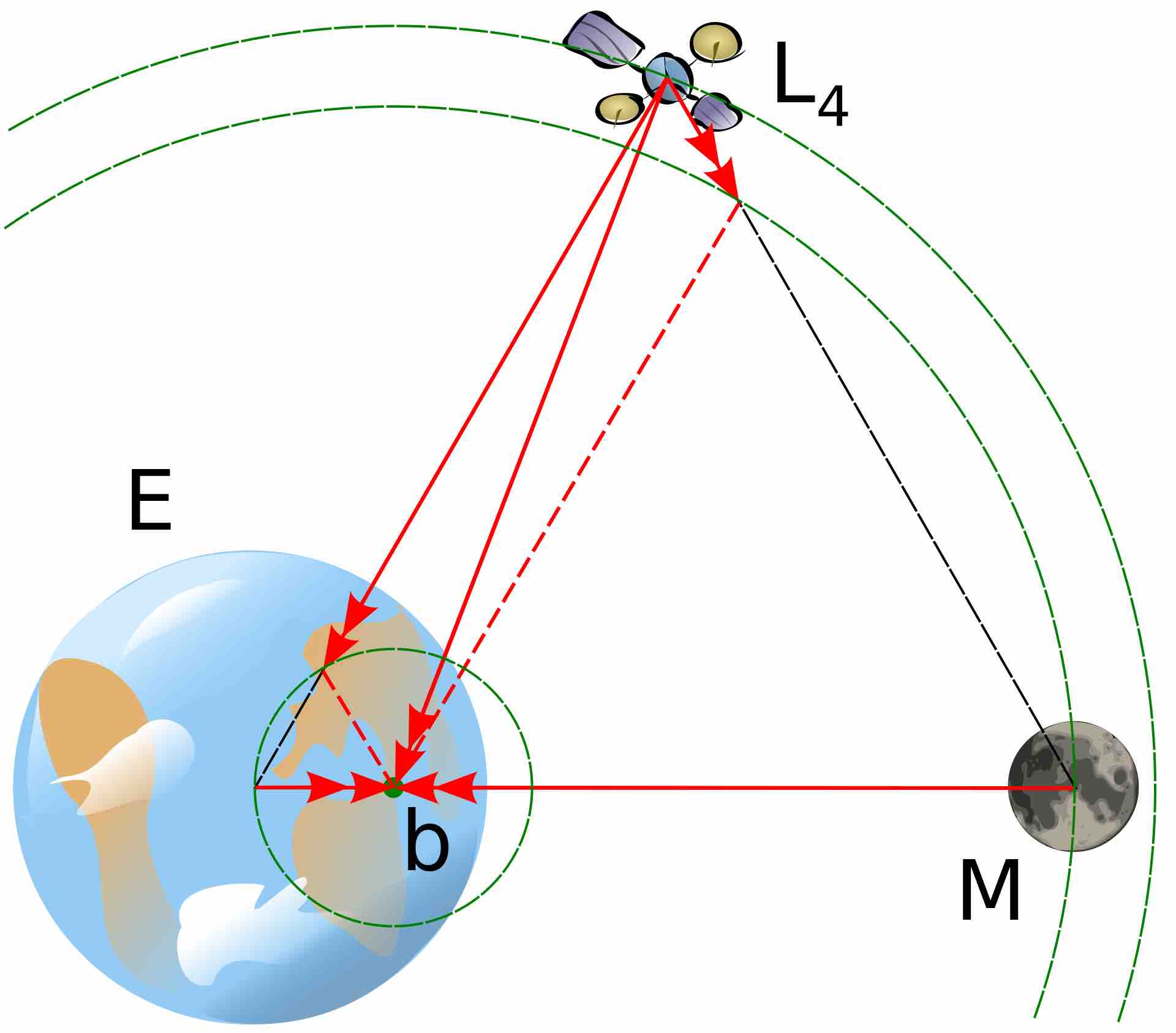
对于拉格朗日点的讨论，更喜欢$$L_{4,5}$$的讨论，简洁、巧妙。
$$\frac{GM_1M_2}{R^2}=M_1a_1$$，得$$a_1=\frac{GM_2}{R^2}$$，同理得$$a_2=\frac{GM_1}{R^2}$$，得$$a_{14}=\frac{GM_1}{R^2}$$,$$a_{24}=\frac{GM_2}{R^2}$$，根据图中几何关系$$\frac{R_1}{R_2}=\frac{M_2}{M_1}$$，$$a_4$$不仅指向双星的质心，由$$a=\omega^2r$$，且满足角速度相同。

如果仅从中学生做题的角度看，只需要掌握在拉格朗日点的卫星和双星具有相同角速度即可。