想象远比知识重要，知识有涯，而想象能环保整个世界。(逻辑带你从A点到B点，想象带你到任何地方。)---爱因斯坦
1、探究碰撞中的不变量
注重实验的引入，注意弹性碰撞动能守恒的特例。
2-3、动量守恒
动量守恒认知的历史过程。笛卡尔最初提出，但他忽略了动量的方向性，后来的惠更斯给出动量守恒的最初表述。牛顿明确用质量与速度乘积来定义了动量。
利用牛顿第三定律和第二定律推导动量守恒。
动量守恒不仅是始末两个状态，而是整个过程一直保持不变。我们才说这个过程动量守恒。
实验证明，高速微观领域，牛顿定律不再适用，但动量守恒依然正确。
电磁波也具有动量，它与粒子的相互作用也遵守动量守恒定律。
动量守恒是一个独立的实验定律，它适用于目前为止物理学研究的一切领域。
4、碰撞
对心碰撞，弹性碰撞，非弹性碰撞，完全非弹性碰撞（损失动能最大，相当于中间弹簧的型变量最大，弹性势能储存最多）
代数法推导。
图像法，共速时，弹簧压缩最大或者是拉伸最大，弹性势能最大，动能损失最多。
特殊情况的讨论。对交换速度的解释。

5、反冲运动，火箭
6、用动量概念表示牛顿第二定律
动量增量的特例解析，类比力学矢量三角形的讲授。
合外力的冲量和某力的冲量对比。

王聪和万炳文两位同学对v-t图像与动量问题的解决方面提供了很好的办法。[?]
对于弹性碰撞模型的解决，等效弹簧，人船模型，相对速度的问题，都有很好的帮助。
以学教学，再发现

在经典力学中，动量守恒暗含在牛顿定律中，但在狭义相对论中依然成立...

角动量是与物体的位置向量和动量相关的物理量。对于某惯性参考系的远点，$L=r\times p$，$L=r\times(\omega\times(mv))$，$L=mr^2\omega=I\omega$
当物体的运动状态（动量）发生变化，则表示物体受力，而作用力的大小等于动量的变化率。$F=\frac{dP}{dt}$（直线运动中，F=ma）（一般物体的动能$E_k=\frac{1}{2}mv^2$）
当物体的转动状态发生变化时，则表示物体受到力矩作用，而力矩就等于角动量的变化率（时变率）$\tau=\frac{dL}{dt}$（旋转运动中，$\tau=I\alpha$）（转动动能$K=\frac{1}{2}=I\omega^2$）
静电力或万有引力均是径向力，因此不会产生力矩。行星运动满足角动量守恒，对应的就是开普勒定律中的第二定律。

动量表示物体达到目前运动状态所获得的全部力的冲量之总和。只有受到力的作用时，这些储存的冲量才会释放出来。
合力 resultant force
质心坐标$R=\frac{\sum r_i\Delta m_i}{m}$

质心速度求解，日本教材上

http://www.qiusir.com/?p=31451

相对质心的速度等效人船模型。

天睿又推荐了一道不错的题目，我用王聪方法画出最后一问。
赵课代表最近问了两道日本的高考题目，挺不错的！

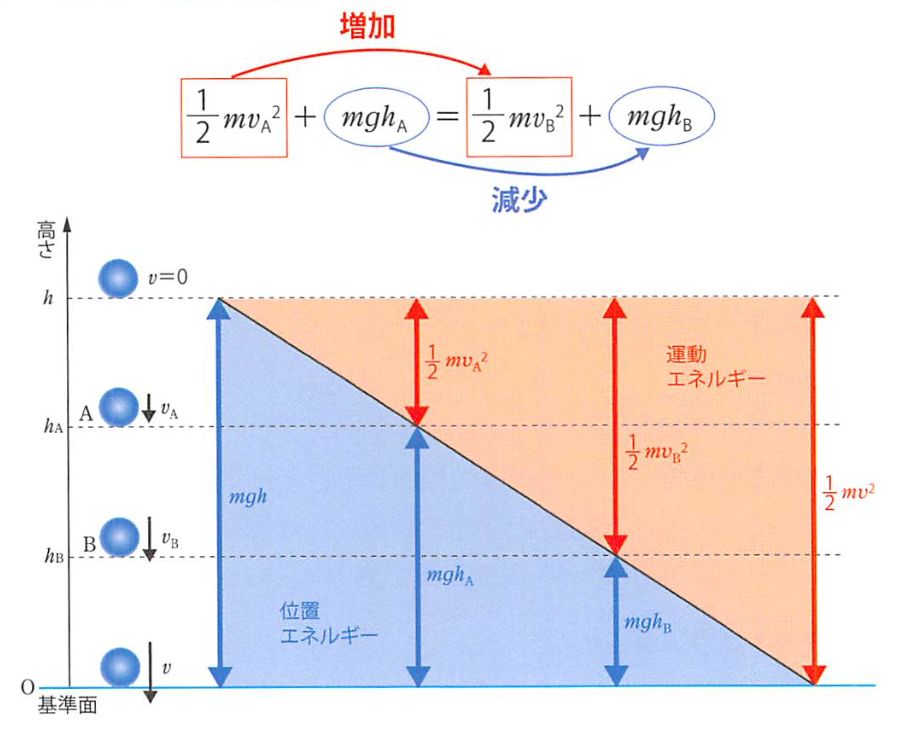
动能定理
势能定理
机械能定理
热量定理
势能（Potential Energy），亦称位能，表示物体在特定位置上所储存的能量。在国际单位制下的单位是焦耳（J），另外在涉及到粒子物理时常用到电子伏特（eV），高斯单位制下为尔格（erg）。势能一般使用“Ep”表示，也常使用“W”“U”和“V”。
通常我们并不在意势能的绝对大小，而是关心其变化量，有时为了计算或者叙述方便，我们也取一个势能零点O，规定O处势能Ep(O)=0，一般选Fcon=0点为势能零点。

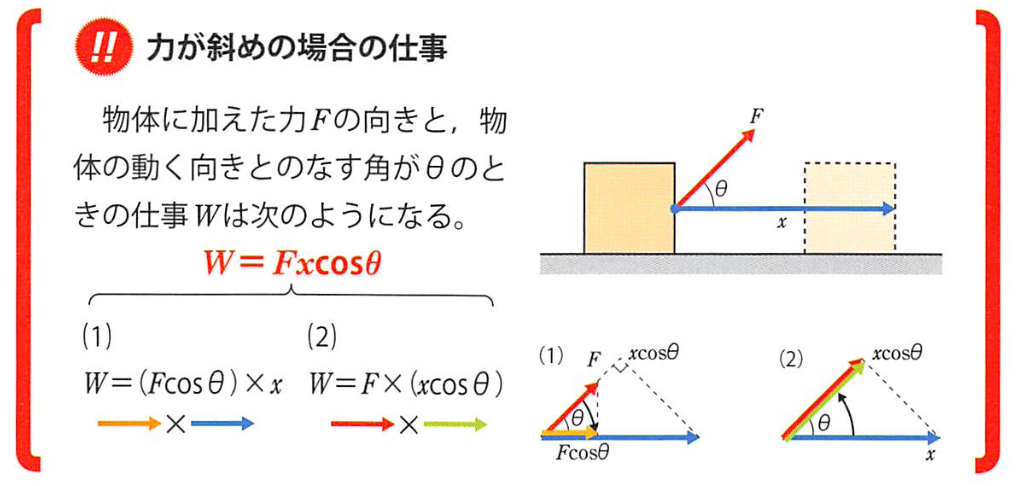
力学的エネルギー保存の法則（力学能守恒定律）

加速过程中做的功，克服以加速度a加速的质量m的惯性力ma所做的功。$s=\frac{1}{2}a\Delta t^2=\frac{(v-v_0)^2}{2a}$由于加速过程中功仅仅与始末速度有关，对于力随时间而变的情况，$W_a=\frac{1}{2}m(v-v_0)^2$也能成立。（物体滑上传送带上产生的热量也是这个公式？）

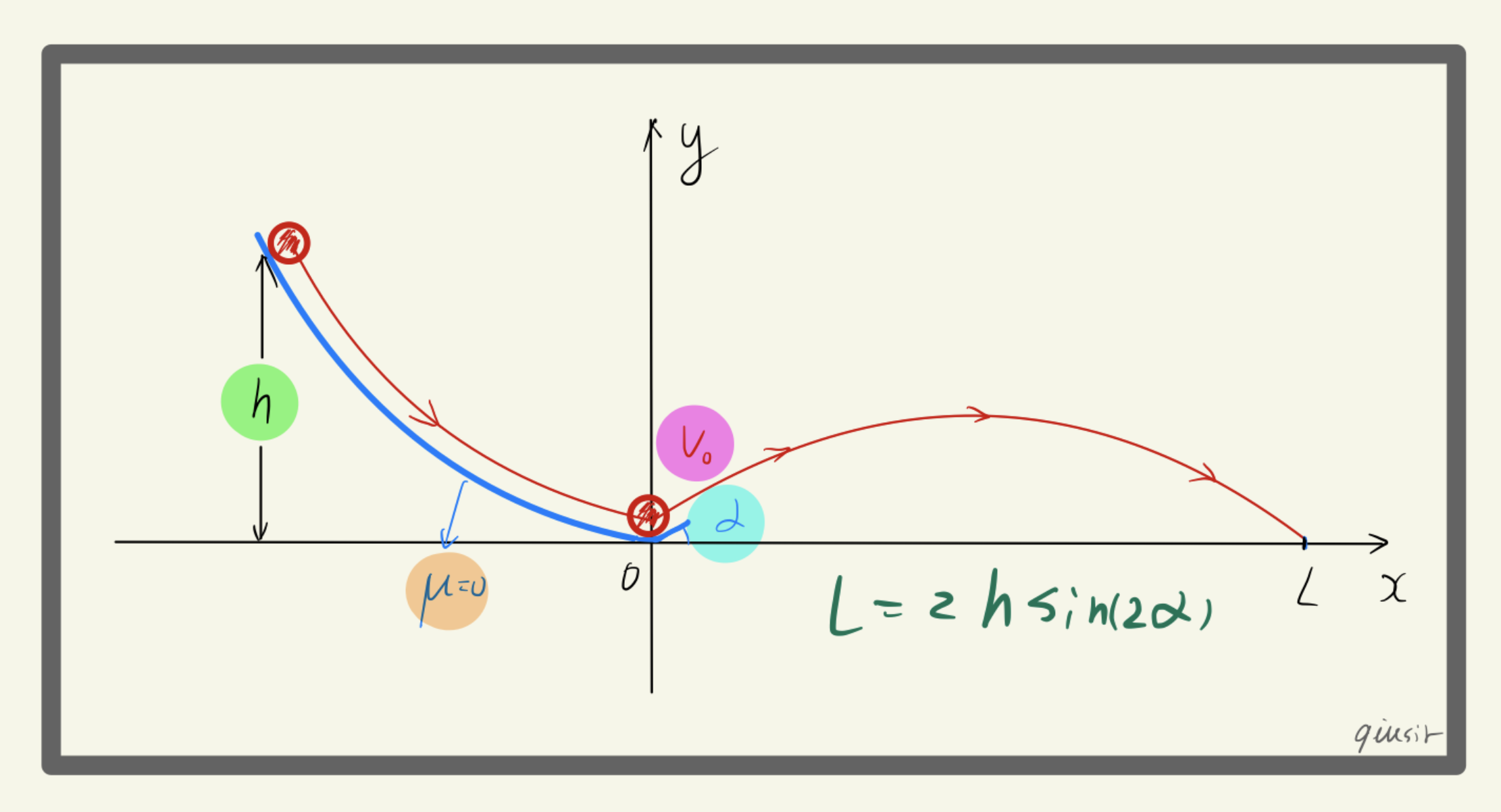
早在Fermat's Library那看到来自1960年R.Sutton的一篇文章[?]的这个简单的实验：让质量为m的小球从光滑斜面上滑下并以仰角α发射，则射程不取决于g，就是说在地球上和火星上是一样的射程。
今天让小胡同学计算了一下...
$mgh=\frac{1}{2}mv_0^2$
$l=2v_0cos\alpha\frac{v_0sin\alpha}{g}$
$l=4hsin\alpha cos\alpha$

万有引力 gravitational force
万有引力定律 law of universal gravitation
波兰的哥白尼去世不久，丹麦的第谷·布拉赫诞生了，1560年14岁在看到了一次日食后便立志要从事天文学相关的工作。
$v=\omega r=\frac{2\pi rad}{24h}\times 6380km=464m/s=1670km/h$
第三宇宙速度（third cosmic velocity)是指在地球上发射的物体摆脱太阳引力束缚，飞出太阳系所需的最小初始速度。在地球轨道上要脱离太阳引力所需的初始速度为42.1公里/秒，但地球绕太阳公转时令地面所有物体已具有29.8公里/秒的初始速度，故此若沿地球公转方向发射，只需在脱离地球引力以外额外再加上适当的动能。
$\frac{1}{2}mv_3^2=\frac{1}{2}mv_2^2+\frac{1}{2}m(42.1-29.8)^2$
$v_3^2=11.2^2+12.3^2=16.7^2$
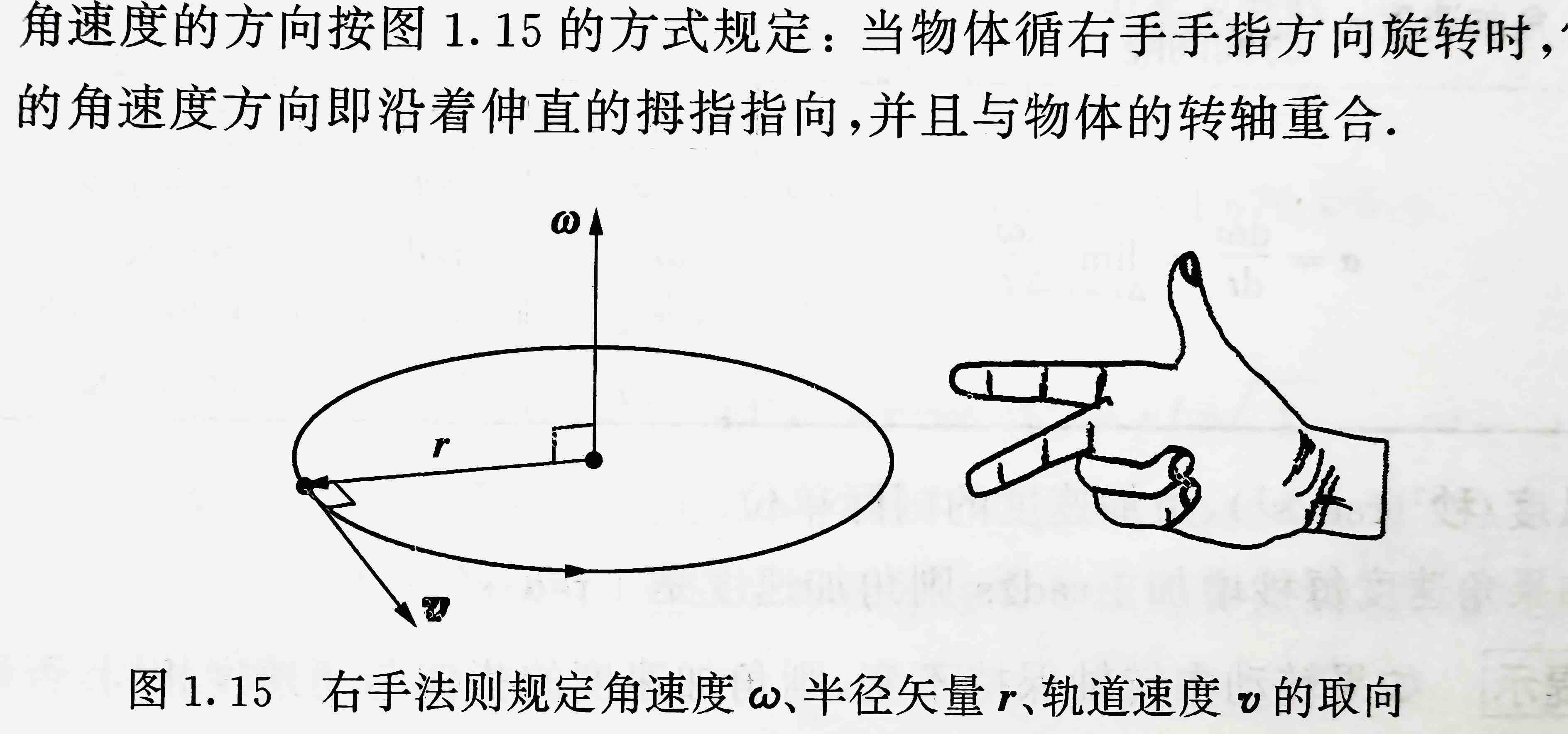
右手三指法则：角速度、半径矢量、轨道速度的方向分别沿着右手拇指、食指和中指的指向。

？第三宇宙速度：从太阳系逃生的速度
约30km/s。R从地球到太阳的距离1.496亿km做吧，M是太阳质量1.989×1030kg做。

第四宇宙速度：太阳系位置的银河系逃生速度
约300km/s。太阳系距离银河系中心约2.8万光年，怎么估计银河系的质量呢？

第五宇宙速度：从银河集团逃出的速度
约1000km/s。银河集团包括到哪个星系？

第六宇宙速度：从宇宙逃生速度
约30万km/s。好像只有光速才能逃脱。宇宙里本来就有“外面”吗？

$a=g(\frac{R}{R+h})^2$、$T=2\pi\sqrt\frac{r^3}{GM}$、$T=2\pi\sqrt\frac{R}{g}$
双星（甚至个别三星模型）$\frac{L^3}{T^2}=\frac{G(m_1+m_2)}{4\pi^2}$
两个相隔数百万千米的物体怎么会对彼此产生力的作用？爱因斯坦认为引力不是一种力，而是空间本身的一个种效应。是物体的质量改变了周围的空间，使空间弯曲，而其他物体则循着这种弯曲空间做加速运动。
引力场强度$g=\frac{F_g}{m}=\frac{GM}{r^2}$
惯性质量$\frac{F_n}{a}$
引力质量$\frac{r^2F_g}{GM}$
关于到底多少颗同步通信卫星能够完全实现全球通信的问题，多数回答三颗。这里谈的更具体一点[?]...

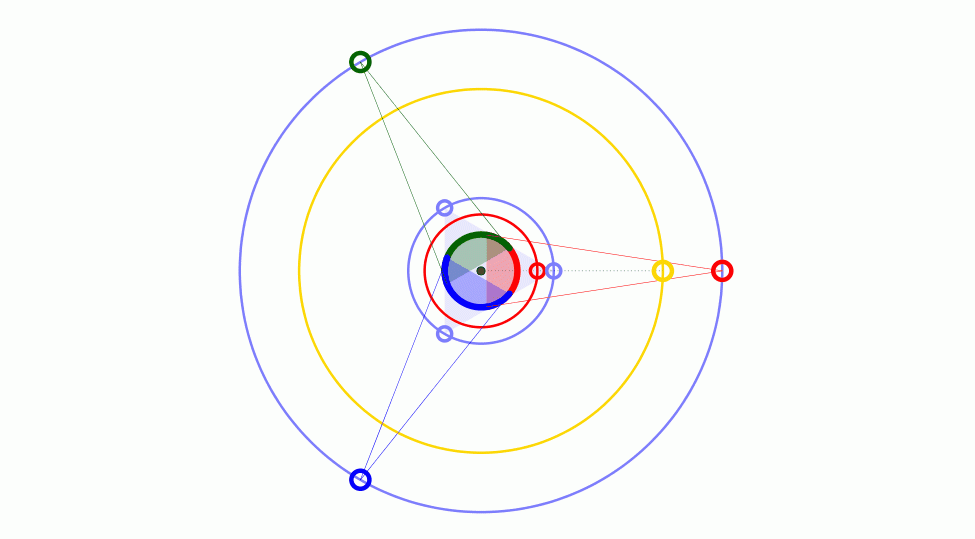
经典问题：
潮汐
拉格朗日点L3

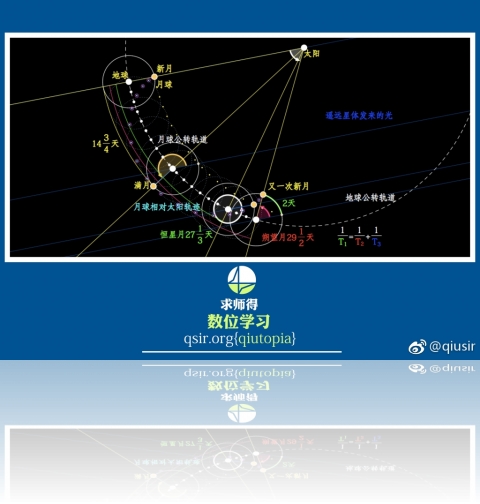
@qiusir:做了一个演示模型，关于月相周期（朔望月synodic，29天多）比月球公转周期（恒星月sidereal，27天多）多…… ​​​​
@qiusir:最近和学生讲万有引力定律的部分，找恒星月和朔望月资料时发现十几年前还算过一个有趣的结论：地球与月球极半径比约为3.66，和π/(4-π)非常近似，就说可以通过构造和地球外切正方形等周长的同心圆来近似构造出月球半径的相对大小。

今年全国II物理高考题（大多数题目算是简单到直接送分，审题和运算甚至高于物理知识的理解）的选择第7题不算简单，如果用我强调过的那个二级公式($\rho=\frac{3\pi}{GT_r^2}\frac{r^3}{R^3}$)要相对省事一些，另外一个也应该重视：$\rho=\frac{3\pi}{GT_0^2}\frac{g_0}{g_0-g}$，当然最简洁的还是$\rho=\frac{3\pi}{GT_1^2}$

二模备选题，卫星平面图看周期以及高度和观测区间。

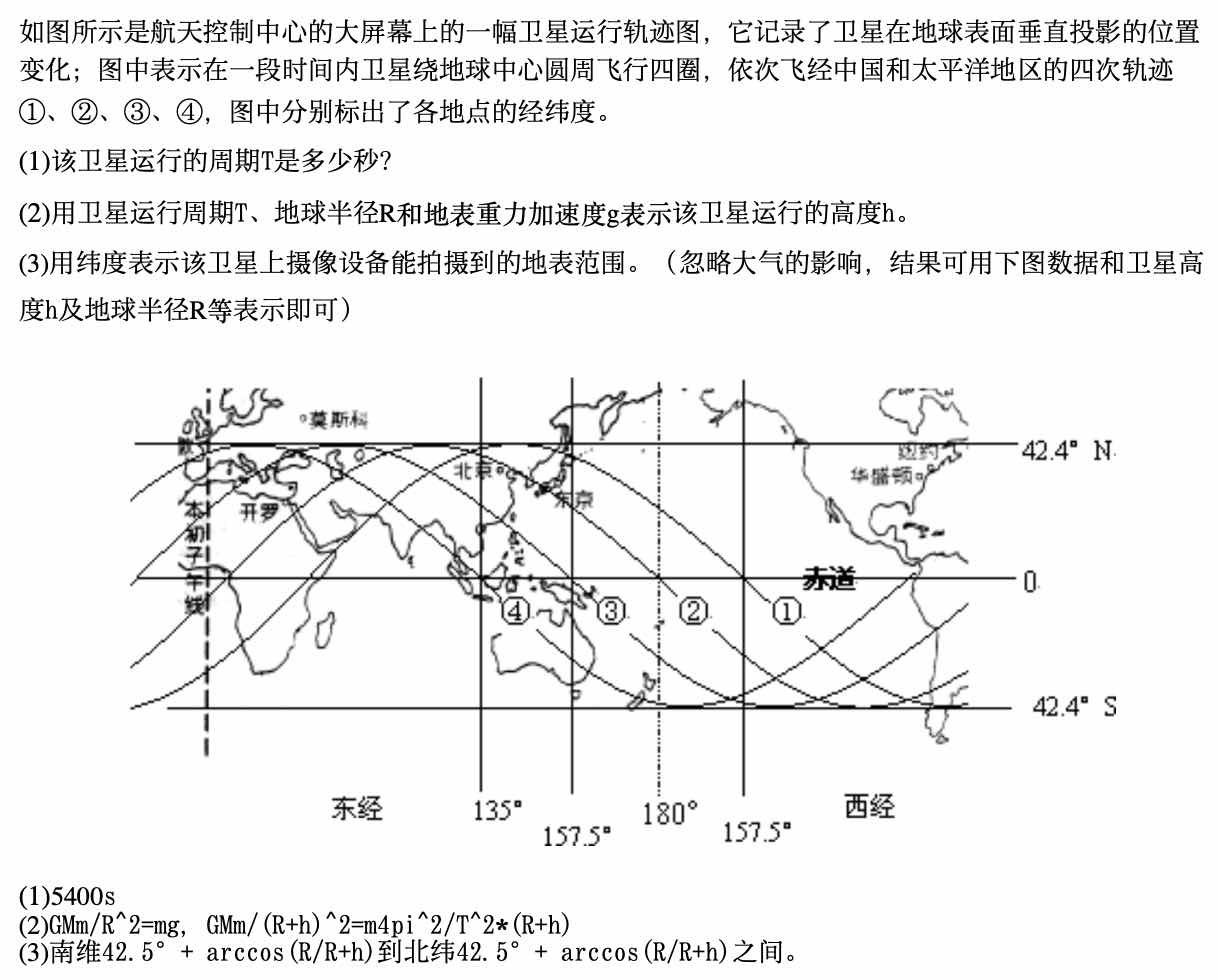
有学生对“地球同步倾斜轨道卫星相对于地面的运行轨迹”的问题很好奇，我抽空构造了简单的模型。要理解太阳的8字舞从这个问题开始会容易不少（有不少的地理知识需要补齐），除了日行迹（sun analemma，太阳在天球一年之中的行踪），当然也有月行迹(Analemma of the Moon)。

8-星行迹 [?]
人造重力[?

午间B班万有引力复习[?]

平面的匀速圆周运动$r(t)=\begin{pmatrix} rcos(\omega t)\\ rsin(\omega t)\\0\end{pmatrix}$，$v(t)=\begin{pmatrix} -r\omega sin(\omega t)\\ r\omega cos(\omega t)\\0\end{pmatrix}$
$a(t)=\frac{d}{dt}\begin{pmatrix} -r\omega sin(\omega t)\\ r\omega cos(\omega t)\\0\end{pmatrix}=\begin{pmatrix} -r\omega^2 cos(\omega t)\\ -r\omega^2 sin(\omega t)\\0\end{pmatrix}=-r\omega^2 r(t)$
0、相对运动 $v_{ab}+v_{bc}=v_{ac}$
1、曲线运动
曲线运动一定是变速运动；曲线运动的物体一定受力；曲线运动可以是匀变速运动。
$\mathbf{a} =\mathbf{a}_{tan}+\mathbf{a}_{norm}=\frac{d(v\mathbf{e}_{tan} )}{dt}=\frac{dv}{dt}\mathbf{e}_{tan}+v\frac{d\mathbf{e}_{tan}}{dt}$
2、运动的合成与分解
交点的速度；同一根绳子／竿上的速度／角速度
渡船问题，如果船的速度小于河水的速度，如此情况下的航行的最小航程。
而沿某一方向可能有两个解。
3、探究平抛运动的规律
抛体projectile，拉丁文pro-向前，ject扔出去
（关于平等，地球对万物的力因为质量不同而不同，但都是具有相同的g，而特别的地区g也不同，这是一种平等的理解）
对匀变速运动物体相同时间间隔内位移增量等于aT^2要更熟练解决，还要对数字有更好的理解。
4、抛体运动的规律
位移和水平的夹角；速度和水平的夹角；相当于从中点发出的。
射程的问题；最高点竖直速度为零。

匀变速曲线运动平均速度$\frac{x}{t}$、$\Delta x=aT^2$的向量性以及和中间时刻瞬时速度等可以从匀变速直线运动迁移过来。
(eg:t=1\3\5经过(0,0)(8,0)(8,6)加速度2.5)

斜抛运动坐标系变换看运动合成。（斜的匀速直线运动和自由落体的叠加）
$L=v_0t$
$x=v_0cos\alpha t=L cos\alpha$
$y=v_0sin\alpha t-\frac{1}{2}gt^2=L sin\alpha-\frac{1}{2}gt^2$
5、圆周运动
$\frac{\Delta r}{r}=\frac{\Delta v}{v}$
两边同除以$\Delta t$
$\frac{\Delta r}{r\Delta t}=\frac{\Delta v}{v\Delta t}$，$\frac{v}{r}=\frac{a}{v}$
6、向心加速度
通过速度的水平和竖直分量的导数，求解出水平和竖直的加速度，求解合加速度。
7、向心力
8、生活中的圆周运动
公路在通过水库泄洪闸下游时常常要修建凹形桥，也叫过水路面。

勾股定理求位移大小后通过平均速度求$v_A$
·一道运动学题目的多种解法[?]
·等速圆周的向心力证明[?]

运动学 静力学 动力学
惯性质量：表示物体对改变它的运动状态的阻抗性。
1、牛顿第一定律
Pope:Nature and nature's law lay hid in night. God said,let Newton be! And all was light.
1687年，牛顿出版《自然哲学的数学原理》
牛顿第一定律是利用逻辑思维对事物分析的产物，不可能用实验直接验证。

2、探究加速度与力、质量的关系
控制变量的方法，m,F
化曲为直的思路。
平衡摩擦力的尺度，小筒质量过大，线段平移弯曲等分析。

3、牛顿第二定律

4、力学单位制
质量，时间，长度。电学是安培。

5、牛顿第三定律
作用力与反作用力一定是同一种性质的力，而平衡力未必。
作用力反作用力的功各种情况都可以。
而摩擦力的功要特殊一些。
6、用牛顿定律解决问题

当物体处于动态平衡时，作用力之和力与静止系中惯性力之和为零。
倾角α的正切值是高度差与水平位移之比，称为梯度。

引力质量与惯性质量相等时被实验证实了的事实，也是广义相对论的出发点。

GHT同学推荐题目：