高中部今晚在小剧场举行了高三励志大会，老师们给高三的学生们打打气...

作为教师，我并不相信成功有什么通用的捷径，我自己也没有预见未来的本领。
但作为长辈，我很确信，竭尽全力的攀登，即便是失败也会八面威风。

无论是作为教师还是作为长辈，我一直都相信，蜗牛的毅力总能丰满隐形翅膀的羽翼。

2011，属于会飞的你！！（唉，一着急，据说口误成2001了...尴尬:()

GSP5文件下载：GSP-平抛运动规律构图 (6768)

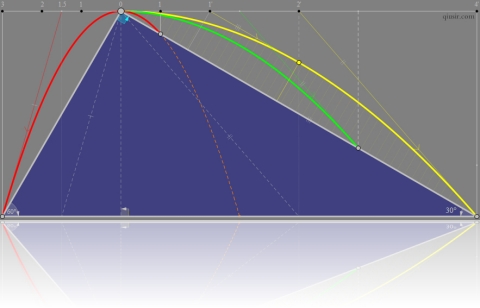
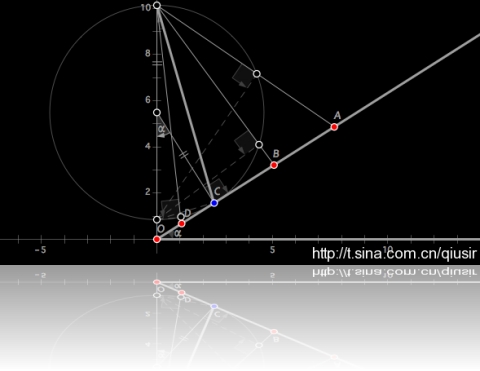
等时圆：滑快从两端搭在竖直放置的圆上的光滑轨道无初速度下滑，且轨道至少一端过竖直方向直径上的一个端点，则下滑的时间相同。因为和圆相关，这里姑且叫做等时圆问题。这个结论很有趣，证明起来也很简单。

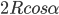设圆半径为R，轨道与竖直方向夹角为$\alpha$，则轨道长度为$2Rcos\alpha$，滑快下滑的加速度为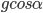$gcos\alpha$，下滑时间为t，所以有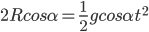$2Rcos\alpha=\frac{1}{2}gcos\alpha t^{2}$，可以看到下滑时间与角度$\alpha$无关，都等于从竖直直径的自由落体的时间。

由上面的结论一样可以设计出很有趣的题目，比如最速轨道的选择问题。说从某点P为起点到倾角$\alpha$的斜面上搭起的光滑轨道中，滑快在哪一条轨道上下滑的最快呢？首先以点P为直径上的一个端点，在竖直方向绘制圆，利用上面的结论，在同一圆上的轨道下滑时间相等，那最短的无非是对应圆的半径最短的了，也就是和斜面相切的那圆对应的轨道。

上图中已经给出很精细的构造，利用几何关系能够知道，与竖直方向夹角为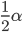$\frac{1}{2}\alpha$的那条就是最速轨道了。

中学物理的习题中经常出现子弹打木块的模型，说光滑水平面上有静止的木块M，被速度为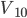$V_{10}$、质量为m的子弹击穿后，子弹和木块的速度分别为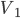$V_{1}$和$V_{1'}$...
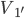这样的题目一般要分别以子弹和木块为研究对象，运用动能定理：
m: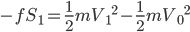$-fS_{1}=\frac{1}{2}m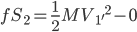{V_{1}}^2-\frac{1}{2}m{V_{0}}^2$，
M:$fS_{2}=\frac{1}{2}M{V_{1'}}^2-0$。
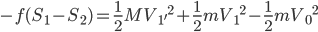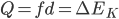两式相加得到$-f(S_{1}-S_{2})=\frac{1}{2}M{V_{1'}}^2+\frac{1}{2}m{V_{1}}^2-\frac{1}{2}m{V_{0}}^2$，
$Q=fd=\Delta{E_{K}}$。以子弹和木块组成的系统为研究对象又有$mV_{0}=mV_{1}+MV_{1'}$。

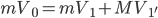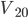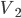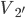若子弹的初速度变为更大的$V_{20}$射击同一木块，击穿后子弹和木块的速度分别为$V_{2}$和$V_{2'}$...设定子弹和木块的相互作用的力恒定。这里会有一系列的小问题：子弹速度增大后是否一定能击穿木块？若能够击穿，则击穿的时间如何变化？木块获得的速度或动能如何变化？子弹损失的动能如何变化？系统损失的动能如何变化？作用力的冲量如何变化？作用力对木块的功如何变化？子弹克服阻力的功如何变化...

这些问题的求解一方面可以通过上述的代数式，更简洁的方式是通过V-t图直接分析...因为木块的厚度为定值，所以图中两个梯形面积相等，所以系统的机械能损失为定值，接下来一系列的问题迎刃而解...这里还涉及到一个有趣的话题，如果把子弹击穿木块后自身能量的减少比作雁过拔毛的话，如何让大雁的毛被少拔一些呢？结果是提高子弹自身的速度。

简单的几条线勾勒出子弹打木块的动态图景，而面积相等的一个等量却形象的表述出相关的参数关系，这样的图示即便是黑板上的简单线条，也能勾起头脑里的具体和丰富的想象。

晚上值班，闲来无事就亲自动手解析了一下曹哥选的题目，其中一道大题涉及到功能关系以及动量守恒定律的，特别需要理解碰撞的细节，物理图景相对复杂...

如下图所示，质量M=3.5kg的小车静止在光滑水平面上，一边靠近桌子，小车上表面与水平桌面相平，小车长L=1.2m，小车左端放有一质量为0.5kg的滑块Q。水平放置的轻质弹簧左端固定，质量为1kg的小物块P置于桌面上的A点并与弹簧的右端接触，此时弹簧处于原长。现用水平向左的推力将P缓慢推至B点（弹簧仍在弹性限度内），推力做功为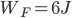$W_{F}=6J$，撤去推力后，P沿桌面滑到小车上并与Q相碰，最后Q停在小车的右端，P停在距小车左端0.5m处（S表示）。已知AB间距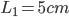$L_{1}=5cm$，A点离桌子边沿C点距离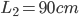$L_{2}=90cm$，P与桌面间动摩擦因数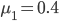$\mu_{1}=0.4$，P、Q与小车表面间动摩擦因数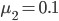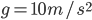$\mu_{2}=0.1$。（$g=10m/s^2$）求：
1）P到达C点时的速度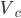$V_{c}$？
2）P与Q碰撞后瞬间Q的速度大小？

初步分析，长度的单位有的是厘米，有的是米，计算中注意用国际单位制；木块与桌面和木块与小车的摩擦系数不同...
过程分析，压缩弹簧过程中，克服弹力做功，而整个过程摩擦力都做负功...
细节分析，物块P先与滑块Q发生碰撞（弹性还是非弹性碰撞？）；中间状态三者匀变速...
具体解析：
1）以物块P为研究对象，在A→B→A→C的整个过程应用动能定理，得：
$W_{F}-\mu_{1}L_{1}-\mu_{1}(L_{1}+L_{2})=\frac{1}{2}m{V_{c}}^2$
$\therefore V_{c}=2m/s$
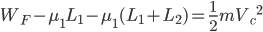
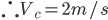
2）设P、Q碰后速度分别为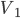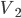$V_{1}$、$V_{2}$，小车最后速度为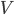$V$，由动量守恒定律得：
$m_{1}V_{c}=m_{1}V_{1}+m_{2}V_{2}$
$m_{1}V_{c}=(m_{1}+m_{2}+M)V$
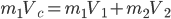
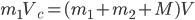
再由能量守恒得
$\frac{1}{2}m_{1}{V_{1}}^2+\frac{1}{2}m_{2}{V_{2}}^2-\frac{1}{2}(m_{1}+m_{2}+M)V^2=\mu_{2}m_{1}gS+\mu_{2}m_{2}gL$
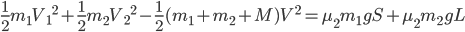
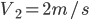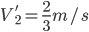
联立解得$V_{2}=2m/s$，$V_{2}'=\frac{2}{3}m/s$
验正，当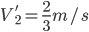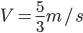$V_{2}'=\frac{2}{3}m/s$，$V_{}=\frac{5}{3}m/s$比前面的Q速度还大，舍去。
$\therefore V_{2}=2m/s$

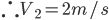
本来觉得很不错的综合题目，虽计算过程多少辛苦些，但结果还是很漂亮...不过大博同学最先发现问题，没想到他竟然要用运动学求解...起初我并没有怀疑题目本身，反倒武断他计算失误了...不过他态度异常坚决...

这些年来还是第一次值班后回家算题的...的确是题目出现了不自洽的错误。通过S=0.5m的相对距离就可以算出数据来，不过就不满足L=1.2m啦:(很是崩溃，怎么给出这样的数据了呢？想来是给出了相对多余的条件，只要机械能损失的和为定值（1.1）就可以...尹同学也做足了功课，早上上班，他还给出了能自洽的数据，改变两个参数的数值：S=0.35，L=1.5m。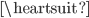$\heartsuit$

所以上面的题目最好更改为：
如下图所示，质量M=3.5kg的小车静止在光滑水平面上，一边靠近桌子，小车上表面与水平桌面相平，小车长L=1.5m，小车左端放有一质量为0.5kg的滑块Q。水平放置的轻质弹簧左端固定，质量为1kg的小物块P置于桌面上的A点并与弹簧的右端接触，此时弹簧处于原长。现用水平向左的推力将P缓慢推至B点（弹簧仍在弹性限度内），推力做功为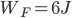$W_{F}=6J$，撤去推力后，P沿桌面滑到小车上并与Q相碰，最后Q停在小车的右端，P停在距小车左端0.35m处（S表示）。已知AB间距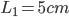$L_{1}=5cm$，A点离桌子边沿C点距离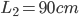$L_{2}=90cm$，P与桌面间动摩擦因数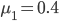$\mu_{1}=0.4$，P、Q与小车表面间动摩擦因数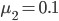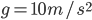$\mu_{2}=0.1$。（$g=10m/s^2$）求：
1）P到达C点时的速度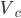$V_{c}$？
2）P与Q碰撞后瞬间Q的速度大小？

有时间也有兴趣的话，可以从运动学角度推演一下，最好是通过V-t图核实一遍数据，上图qiusir给出更改参数后对应的一组数值。也真难为孩子了，等天气好些了，带上大博和尹同学，还有以及我的课代表，出去犒劳一下。