这是一篇受密码保护的文章，您需要提供访问密码：

密码：

（和MingsongHu一起重新构造了拉格朗日点s）
在了解拉格朗日点之前，应该先对双星系统有所知晓。为了方便，把双星系统中大质量的称为恒星，质量$M_1$，比如太阳；小质量的称为行星，质量$M_2$，比如地球。
由$\frac{GM_1M_2}{R^2}=M_1\omega ^2 R_1$，$\frac{GM_1M_2}{R^2}=M_2\omega ^2 R_2$，
得$\frac{R_1}{R_2}=\frac{M_2}{M_1}$，$\omega^2=\frac{G(M_1+M_2)}{R^3}$
双星以相同角速度围绕质心（到旋转中心距离与质量反比）旋转，角速度由质量和距离决定。

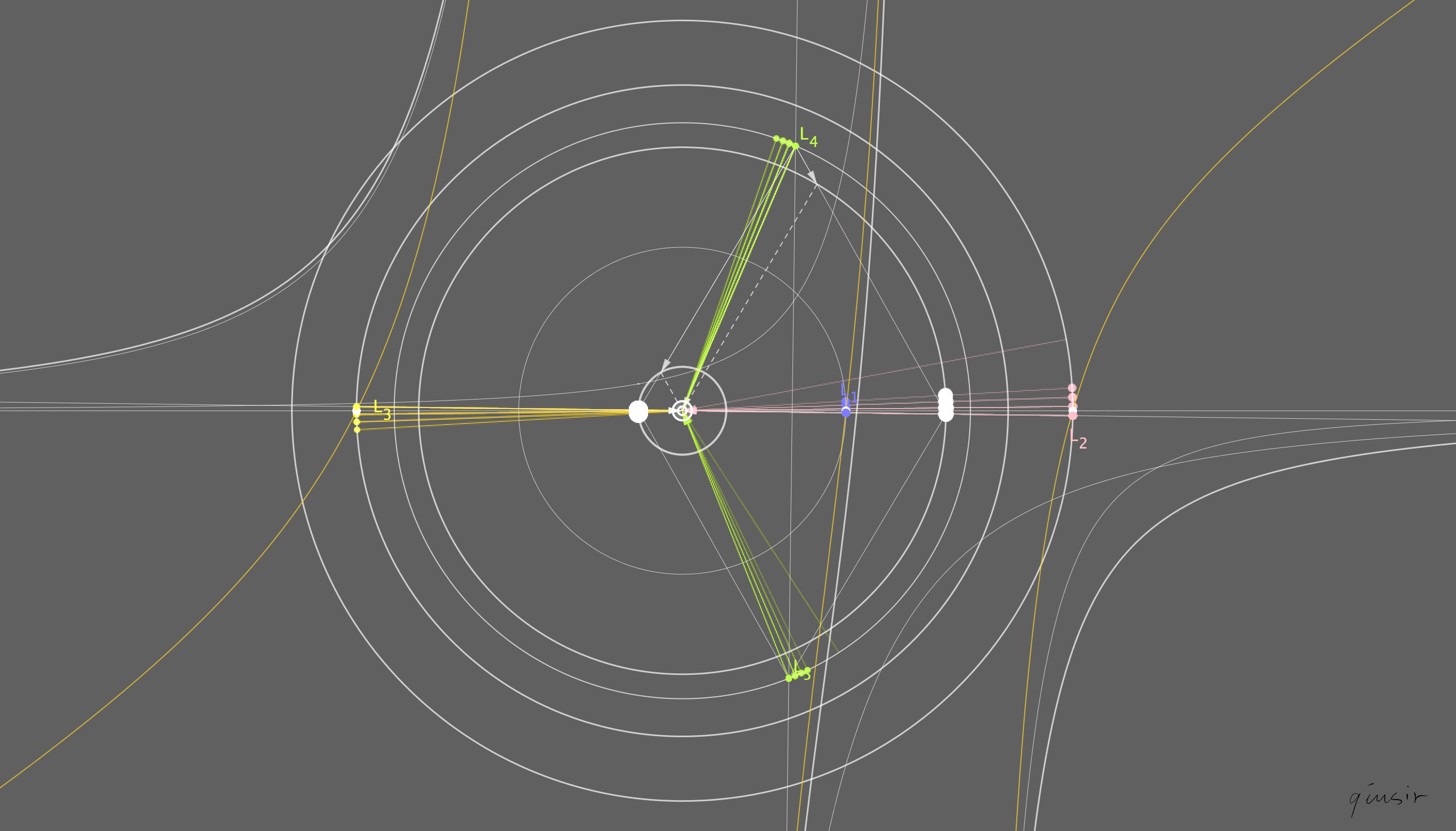
在双星系统中引入第三个天体，为同前面统一，这里称卫星，由于$m< <M_2$，对双星系统运动影响忽略，就如人造地球卫星对地球和月亮的运行的影响可以忽略一样。在双星系统的二体引力场中，数学家欧拉和拉格朗给一共推算出了5个特殊的位置，能让第三个物体与另两个天体的相对位置保持不变，即在双星系统的非惯性系中，卫星的加速度为零。 对于$L_1$，原本与恒星距离越近角速度越大，但由于有行星的引力抵消一部分，使卫星以行星的角速度运行成为可能。$r$为卫星与行星距离。 $\frac{GM_1m}{(R-r)^2}-\frac{GM_2m}{r^2}=m\omega^2(\frac{M_1}{M_1+M_2}R-r)$ 化简得$\frac{M_1}{(R-r)^2}=\frac{M_2}{r^2}+\frac{M_1}{R^2}-\frac{M_1+M_2}{R^3}r$ 对于$L_2$，同理，原本与恒星距离越远角速度越小，但由于有行星的引力参与增强了一部分，使卫星以行星的角速度运行成为可能。$r$为卫星与行星距离。 $\frac{GM_1m}{(R+r)^2}+\frac{GM_2m}{r^2}=m\omega^2(\frac{M_1}{M_1+M_2}R+r)$ 化简得$\frac{M_1}{(R+r)^2}+\frac{M_2}{r^2}=\frac{M_1}{R^2}+\frac{M_1+M_2}{R^3}r$ 卫星在双星系统的离心加速度（非惯性系的离心力所对应的加速度）$a_c=\omega ^2(r-\frac{M_2}{M_1+M_2}R)$，$a_c=\frac{G(M_1+M_2)r-M_2R}{R^3}$ 对于在双星连线上的拉格朗日点，可以利用相对加速度为零求解（图）。$a=-\frac{GM_1}{r^2}sgn(r)+\frac{GM_2}{(R-r)^2}sgn(R-r)+a_c$

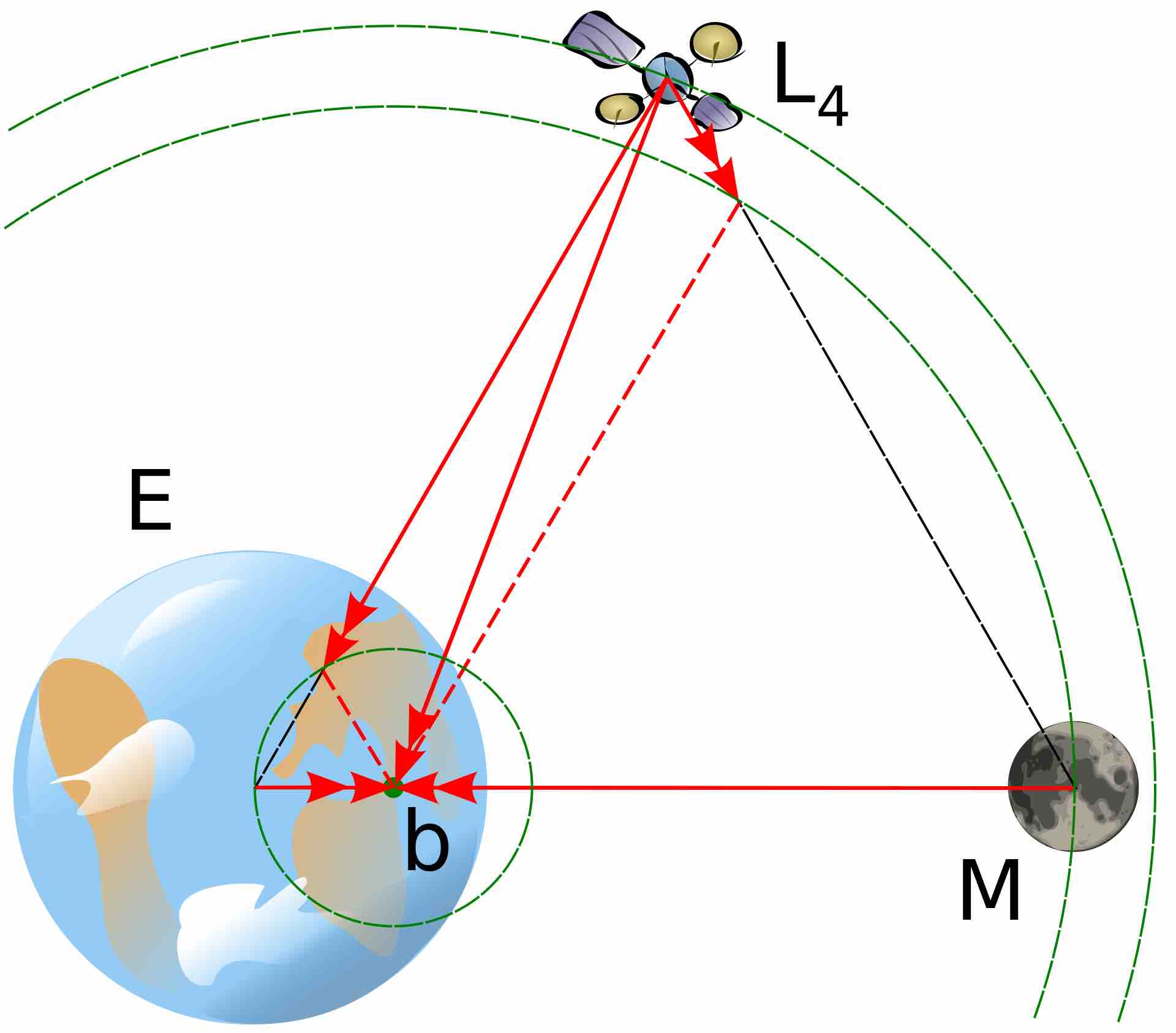
对于拉格朗日点的讨论，更喜欢$L_{4,5}$的讨论，简洁、巧妙。
$\frac{GM_1M_2}{R^2}=M_1a_1$，得$a_1=\frac{GM_2}{R^2}$，同理得$a_2=\frac{GM_1}{R^2}$，得$a_{14}=\frac{GM_1}{R^2}$,$a_{24}=\frac{GM_2}{R^2}$，根据图中几何关系$\frac{R_1}{R_2}=\frac{M_2}{M_1}$，$a_4$不仅指向双星的质心，由$a=\omega^2r$，且满足角速度相同。

如果仅从中学生做题的角度看，只需要掌握在拉格朗日点的卫星和双星具有相同角速度即可。

带电粒子（不计重力）从平行板电容器中间水平入射，电容器两板之间加方波电压（静态看，也可以暂时把电压考虑成电量，但电量的好处是调整板间距离电场力不变，加速度不变），且$v_0=\frac{L}{T}$，即带电粒子在电容器内穿行的时间为一个周期$T$...（另一类题目是初速度很大，即$\frac{L}{v_0}\sim 0$，带电粒子在电容里运动看作类平抛...）

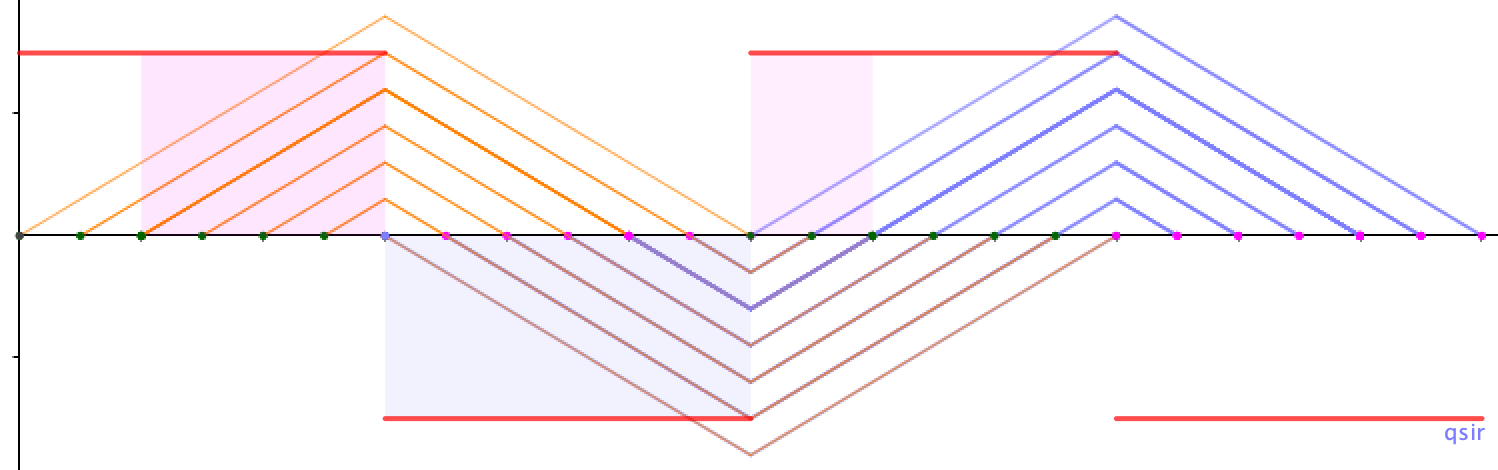
以正负电压相等为例，电压图像可以转化为加速度时间图像，由于运行时间为一个周期，速度变化量相同，或者说用竖直方向动量定理（或从加速度时间图像的面积不变来考虑），出射粒子竖直速度为零，即粒子都水平射出。

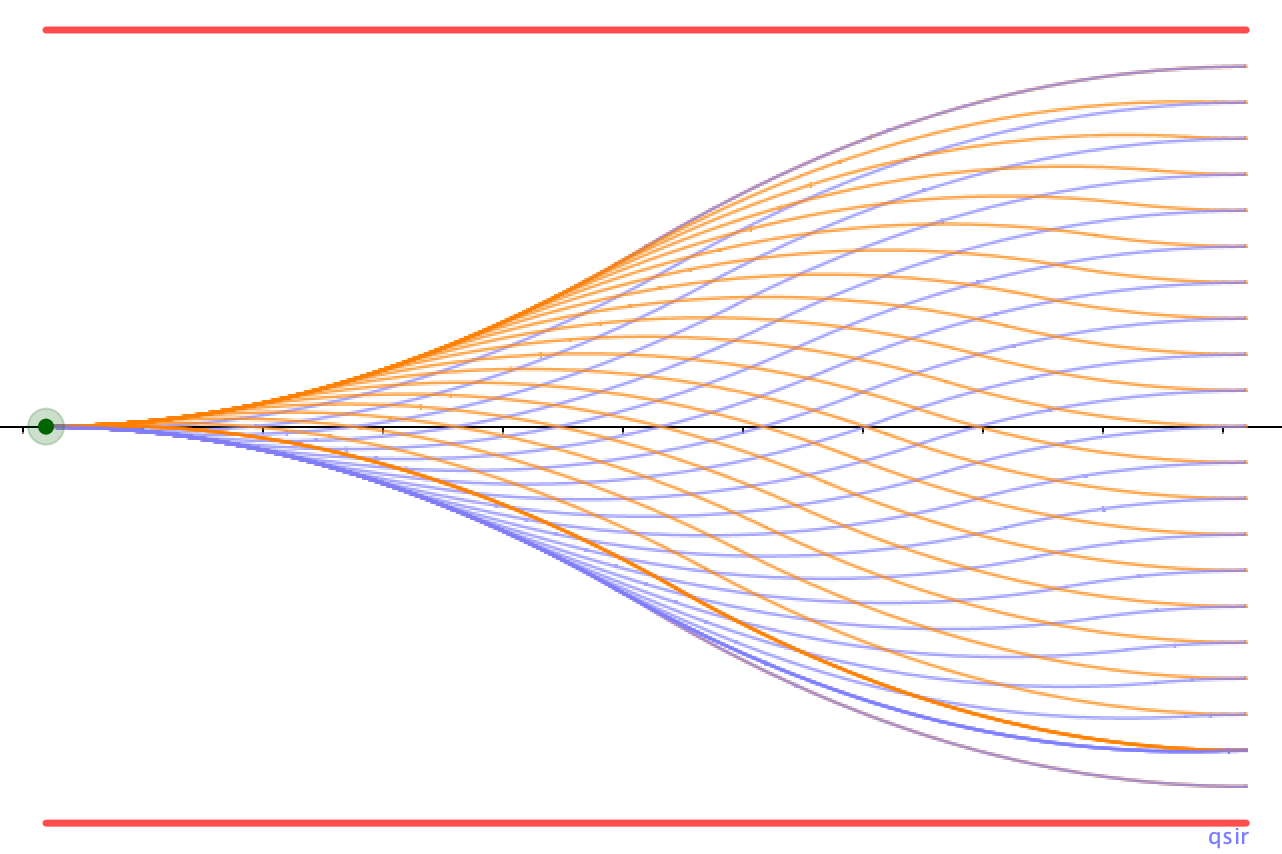
而对于粒子的运动轨迹，除了末速度水平以外，出射点位置关于$\frac{T}{2}$对称，且为线性。以粒子入射时刻$\frac{T}{2}\pm t$，$y=\frac{4aTt-aT^2}{4}$（这是射出时数值偏移量，但未必是最大数值偏移量，后面用到。）

有趣的是，前面的结论在更一般一点的情况下也有成立，如果把正向电压$U_1$转化为$a_1$，反向电压$U_2$转化为$a_2$，半周期还是对等，运行时间还是一个周期，那射出速度$v_y=(a_1-a_2)\frac{T}{2}$，$y=\frac{a_1T^2-3a_2T^2+4(a_1+a_2)Tt}{8}$

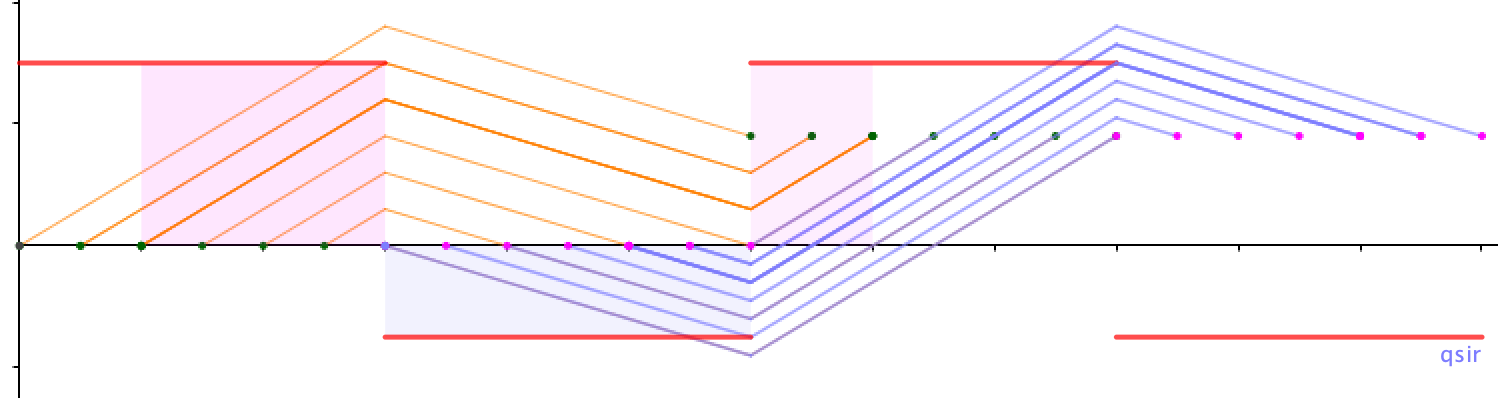
从初设轨迹上能很直观看到，射出粒子速度相同，入射时间关于$\frac{T}{2}$对称时，也如前面，运行轨迹不同但出射点位置相同。

对于正反电压相同的情况下，中间入射的粒子仍从中间射出，入射时间分别是$\frac{1}{4}T$和$\frac{3}{4}T$，而对于对于正电压是反电压2倍的情况下，中间入射的粒子仍从中间射出，入射时间分别是$\frac{5}{12}T$和$\frac{7}{12}T$（正反电压不同是一道不是很轻松的计算题目，要动笔算算）。但都是关于$\frac{1}{2}T$对称的。

真正促使我用整整一个晚自习来整理相关内容，还是那位喜欢打篮球且篮球打得很好的王同学问的一道看起来不难的问题，我一直怀疑是不是什么竞赛题目。主要的是对这个问题解决的过程中，复习了不少运动学知识，也遇到一些主动的问题。

正反电压同为$U_0$，粒子从电容器两板中间入射，且粒子在电容器内部运行的时间正好是一个周期（如前面讨论的$T=\frac{L}{v_0}$），问板间距离是多少能使入射粒子的50%从电容器另一端射出。

要解决这个问题，先要思考如下几个小问题。
1、保证$\frac{T}{4}$时刻入射的粒子还能从电容器另一端的中间射出，板间距离是多少。$d=\frac{1}{2}a{(\frac{T}{4}})^2\times2\times2$

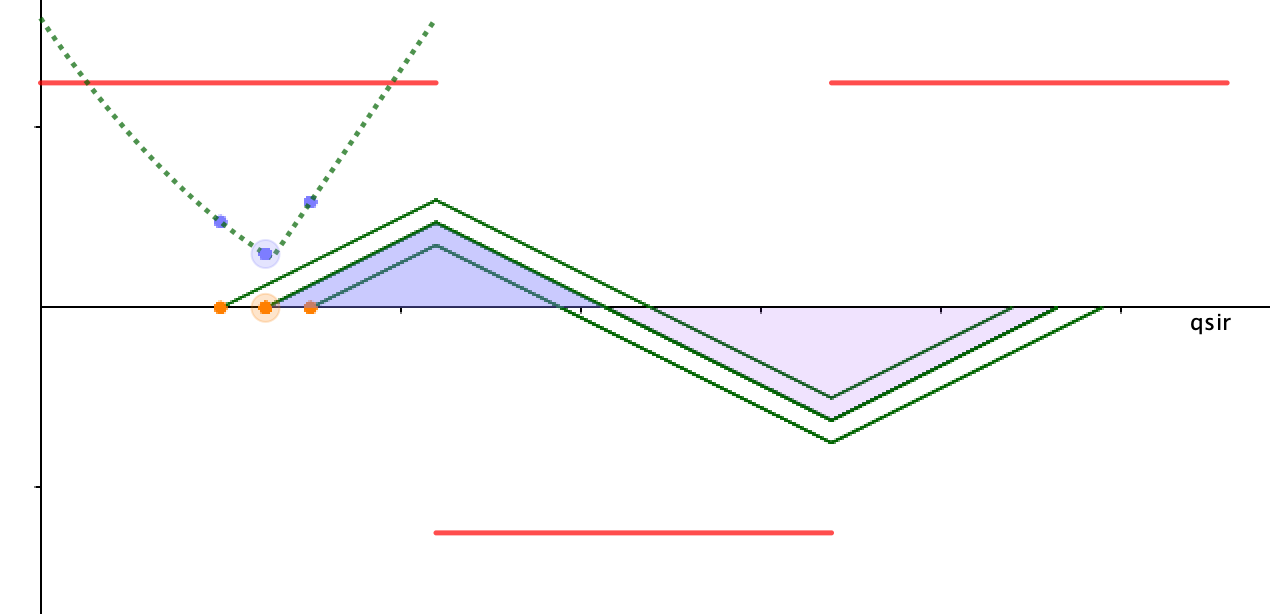
2、中间入射的粒子能从电容器另一端射出，板间距离是否有最小值。
这个问题最先是溢成同学最先在课上提出，若云最先是直觉判断那两个三角形面积为1：2时，即向上和向下偏离入射方向相同的时候板间距离最下，单一同学给出很好的几何解释，崔刘同学也独立给出求解。现在看，可以通过一个二次函数与一个一次函数取大的交点来求解。（粒子是从中间入射，向上偏或向下偏移的距离都得满足才可）（入射向上偏移的距离是和入射时刻的关系是二次函数，入射到出射整个过程的数值位移是和入射时刻的一次函数）

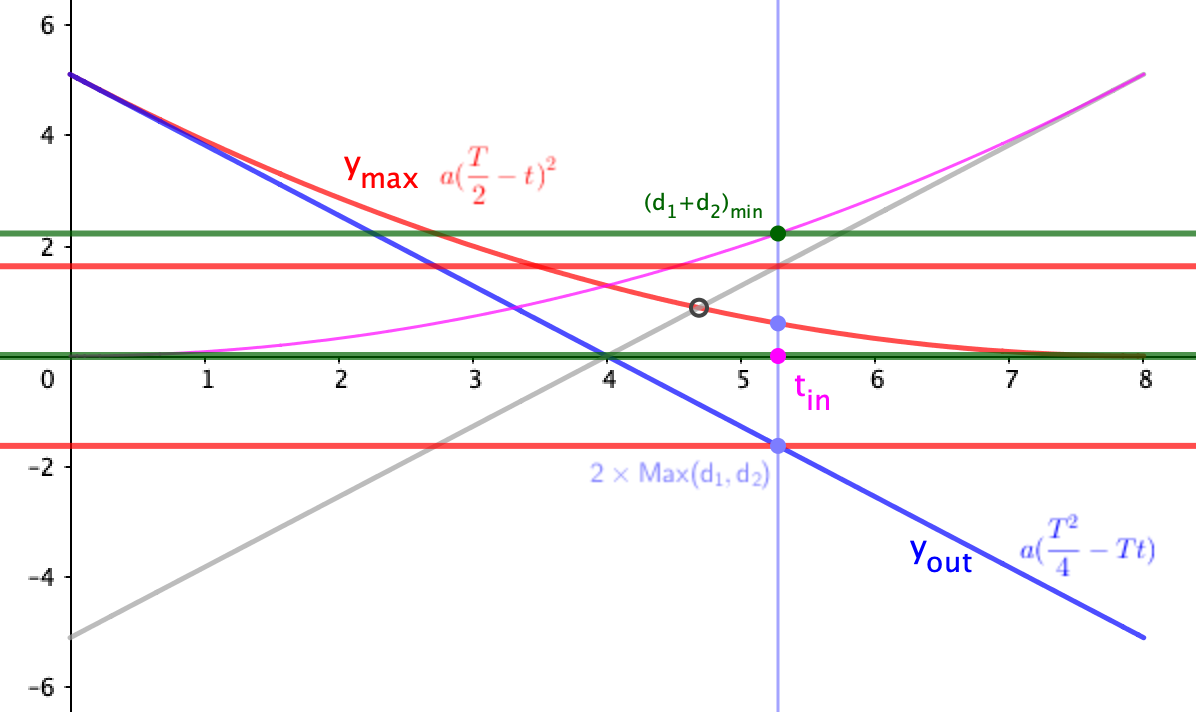
（分段取最大的问题）（间距极值问题，贴边入射和中点入射。一个是$\frac{T}{4}$，一个是$\frac{2-\sqrt{2}}{2}T$）
3、水平入射的粒子能够出射，板间距离最小值是多少。（并没有入射粒子在中间这个前提）（向上偏移和向下偏移的和的极小值。）

4、如果从时间分布上看，出射粒子偏离入射方向最近的50%，有一半对应的是$\frac{1}{8}T$到$\frac{3}{8}T$，而这样考虑，首先能想到的错误是，粒子在竖直方向偏离的最大位置是在射出前出现（竖直速度为零的位置也是竖直最大距离处），对应前面的二次件数与一次函数的表达，容易理解一点。
5、晚自习推荐给物竞的欣然同学，早上他一次性给出了很完备的解释，向同学最早有自己的正确的想法，引发了我更多的考虑，若云同学给出更多解释和正确和工整的计算，庆林同学也给出正确计算。当然这个问题的核心在竖直偏离的最大位置关于入射时间的关系是一个二次函数与一次函数的最大问题。

宋明屿同学一早算出：$t_1=\frac{2-\sqrt{3}}{2}T$（$t_2=t_1+\frac{1}{4}T$，另一部分是延后$\frac{1}{2}T$射入），板间最小距离$d=(2-\sqrt{3})\frac{U_0q}{md}T^2$。孙浚豪同学和逍遥老师班上的同学也给出相同的结果。
6、可以尝试更一般的计算，比如反向电压是正向电压的一半，不考虑入射点位置是否在中间，保证所有粒子都射出，板间距离是多少。（编写这个题目时就觉得不容易，也正是对这个模型熟知，对前面的问题定势了不少，忽视分段函数及最值等细节，造成求解麻烦。）
7、如果在更一般情况下，出射粒子占入射粒子20%...
8、（当初记录的就不条理，除了切入题目难之外，也是遗忘等因素。一年后再次做了这个题目也不是很容易，当然最主要的原因是对于代数计算的重视不够，想通过图像一蹴而就反而增加了认知难度。20220505）
在整理这道题的过程中，打完羽毛球的家麟同学来办公室推荐一道物理题，然后一起作图休息，他傍晚要模考两科，下班路上，王老师嚷着说那本练习册特别，其中也有这道题目，哈哈哈

附宋明屿同学的计算过程[?]：

关于带电小球在匀强磁场中的运动，也可以转化为带电粒子在正交匀强电场和匀强磁场中的运动模型。正电q质量m小球在垂直纸面向里的匀强磁场中静止释放，设运动中下落最大高度$h_m$和能获得最大速度$v_m$...
思路1（记得是很多年前，课代表杨洛的思路）
由于只有重力做功（洛伦兹力始终不做功），下落最大高度和最大速度对应；同时，由于是下落最大高度时速度最大，那$v_m$一定是水平的（$v_y=0$）。根据动能定理和水平方向动量定理，可得：
$mgh_m=\frac{1}{2}m{v_m}^2-0$
$\sum Bq v_y \Delta t=mv_m-0$
$Bqh_m=mv_m-0$
联立解得$v_m=2\frac{mg}{qB}$ $h_m=2\frac{m\frac{mg}{qB}}{qB}$

思路2（参考资料上通常给的方法，学生印象深但理解的一般）
静止释放的小球看成是由两个大小相等方向速度的叠加，而特别选取$v_0=\frac{mg}{qB}$，主要的意图是水平向右的速度对应的洛伦兹力能平衡掉重力，这样，带电小球的运动就可以转化为逆时针圆周运动与水平向右匀速直线运动的合成，轨迹是摆线。
至于最大速度和下落最大高度，半个周期时，圆周运动与水平匀速运动速度方向相同，和速度最大$v_m=2\frac{mg}{qB}$，而下落最大高度$h_m=2r$

思路2（建立在思路2）
既然能把运动简化为圆周运动和匀速直线运动的合成，那利用圆周运动在直径上的投影为简谐振动这一点，可以知道带电小球在竖直方向是简谐振动（匀速直线运动不影响竖直方向）。利用简谐振动的最高点和最低点加速度相同，$qBv_m-mg=mg$,得$v_m=2\frac{mg}{qB}$...

思路1的代数法简洁，思路2这里叫几何法的话，很直观，思路3利用二级结论巧算最大速度。这道题目很有趣的地方还在于其初速度的开放性和运动的轨迹的规律性有很好的统一。比如一个周期内的水平跨度，$d=\frac{mg}{qB}T$，$T=\frac{2\pi m}{qB}$，再比如，如果小球的初速度是倾斜的，通过上图应该可以想到，运动的轨迹是水平的$v_0=\frac{mg}{qB}$和小球初速度与$v_0$矢量差为线速度的圆周的叠加，当然回过头看，前面的讨论不过此前提下的是特例。

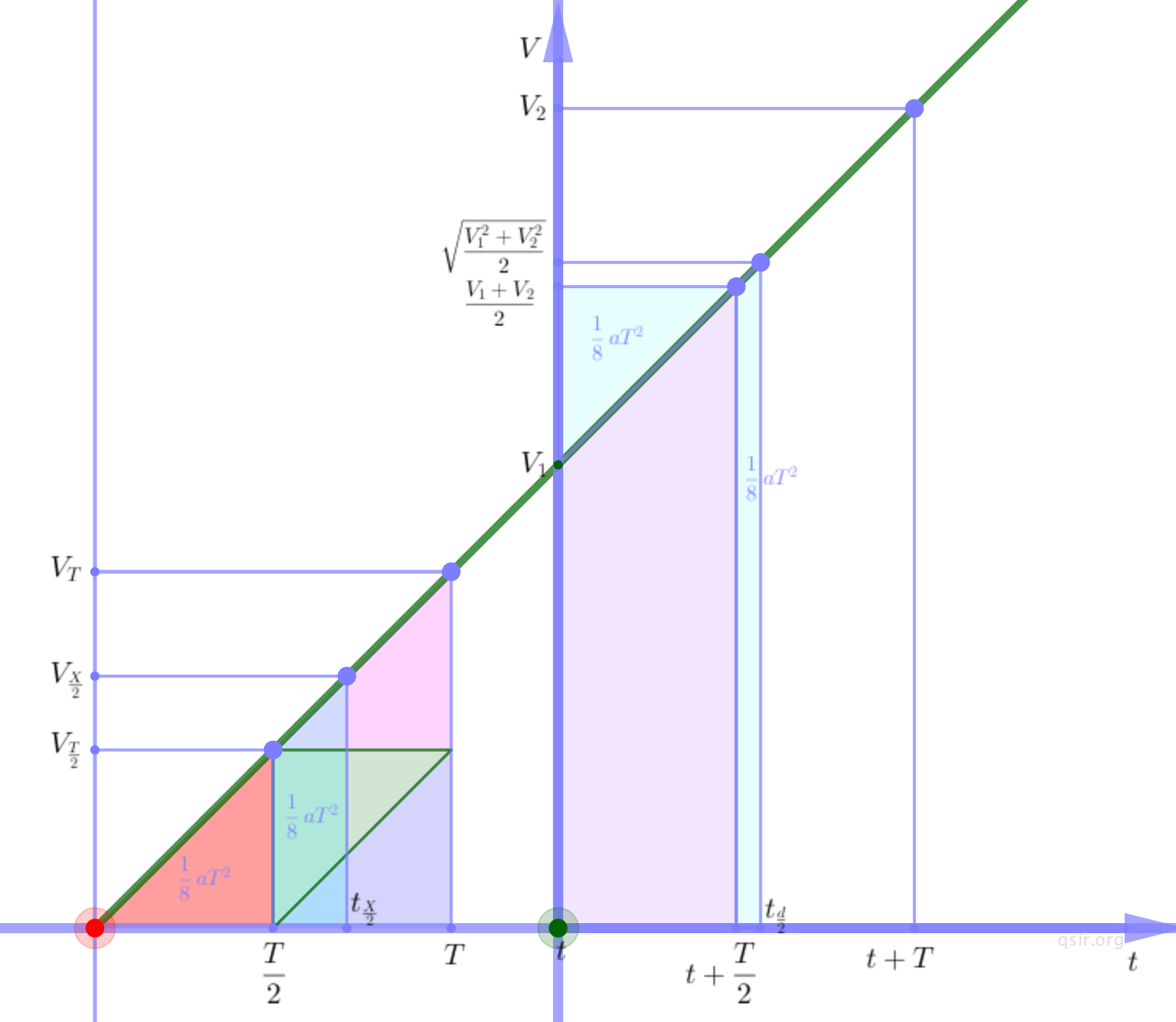
最近才主要关于匀变速运动位置中点到中间时刻的位移的结论竟然如此奇妙:$\frac{1}{8}aT^2$。有了这个精简的结论，分析用光电门测量物体减速度的误差问题就要容易很多，而更值得珍惜的是这个认知过程中学生和老师的协力发展。

已知物体匀加速通过两个距离为L的光电门，遮光片宽度为d，通过两个光电门所需时间分别是$\Delta{t_1}$和$\Delta{t_2}$。用这种方法测的加速度为$a=\frac{(\frac{d}{\Delta{t_2}})^2-(\frac{d}{\Delta{t_1}})^2}{2L}$，而这个问题的难点是对于用这种方法测量加速度的系统误差是偏大还是偏小（忽略偶然因素的影响）。
首先应该明确的是L是两个光电门的距离，也是两个遮光片中点处经过光电门的距离，而上述方法用到的速度是遮光片经过光电门的平均速度，也是中间时刻的速度，应该用中间时刻间的位移而使用的是中间位置的位移，这是系统误差产生的原因。
从应试看，毕竟只是一个二选一的填空，最初我只是采用近似法进行系统误差分析的，速度更快时经过光电门时，中间位置和中间时刻更接近，算是次要因素（也不严谨，尽管时间差小但速度差大）。从速度时间图像看，中间时刻间的位移大于中间位置的位移，所以系统误差是测得的加速度偏大。后来才注意到这本身就是一道很不错的运动学题目。
这几年大概有几个学生对这个问题有着自己很不多的探究。

崔家瑞
少儿班化学竞赛学生，求师得数位学习的大将。记得崔同学竟然设了四个速度，但结果又很简答，代数的力量感现在还有印象。为了简化，这里就分析经过第一个遮光片的情况就好。
初速度$v_1$，末速度$v_2$，中间时刻的速度$v_{\frac{t}{2}}=\frac{v_1+v_2}{2}$，中间位置的速度$v_{\frac{x}{2}}=\sqrt{\frac{v_1^2+v_2^2}{2}}$，
$\Delta{x}=\frac{v_{\frac{x}{2}}^2-v_{\frac{t}{2}}^2}{2a}$，整理的，$\Delta{x}=\frac{(v_2-v_1)^2}{8a}$
张宸溪
直升班开朗的男孩，初三直升的学生有耐心用基本的公式进行运算，这是学生最应该用的方法。借助图像更容易理解。
$\frac{1}{2}(v_1T+\frac{1}{2}aT^2)-v_1\frac{T}{2}+\frac{1}{2}a{\frac{T}{2}}^2$
整理后得，位置中点与中间时刻间的距离$\Delta{x}=\frac{1}{8}aT^2$
阿布都旭库尔
肖遥老师在去食堂的路上和我说起新疆部有学生发现的一种方法，觉得很好，吃饭的时候还在讨论，的确很巧妙，而我的记忆力第一次出现新疆学生的奇思妙想，这算是我花时间整理这个知识点的动力之一。
他用到$\Delta{x'}=a(\frac{T}{2})^2$，即相邻时间间隔内位移差，而我们要求解的是中间位置和中间时刻的距离，应该是刚才这个差值的一半，即只有从中间时刻的位置后撤刚才的位移的一般才能保证是位置的中点。$\Delta{x}=\frac{1}{2}a(\frac{T}{2})^2$
徐川皓
毕业许久的徐同学除了在说说上总给我点赞，还鼓励过我坚持自己的教育理想。我记忆中他可是很内敛的学生，而一次课上讨论这道加速度误差的问题，他想到的是面积割补的方法，现在印象还是深刻。中间位置与中间时刻的位移转化为中间时刻与速度轴的三角形面积，结论一目了然。

任泉羽
理科部学生会的“老干部”，学习踏实诚恳，这是可是学习品质中的大聪明，他对于特殊情况的分析其实也很有意义。就是如果初速度为0，前一半时间和后一半时间的位移是1和3份，而中点当然前后是2份，那中间时刻和中点的位移自然是1份了，也就是位移的$\frac{1}{4}$，从这个角度看，前面的结论可以看成是$\Delta{x}=\frac{1}{4}\frac{1}{2}aT^2$，从一种特殊情况看到这个规律竟然有通用性。

边思羽
分别设定第一次遮光结束时的速度$v_1$和第二次遮光结束时的速度$v_2$，$d=v_1t_1-\frac{1}{2}a{t_1}^2$，$d=v_2t_2-\frac{1}{2}a{t_2}^2$，利用$a=\frac{{v_2}^2-{v_1}^2}{2l}$，并由前两式代入化简可得，$a<\frac{(\frac{d}{t_2})^2-(\frac{d}{t_1})^2}{2L}$ 如果是测减速运动的加速度，结论相反。