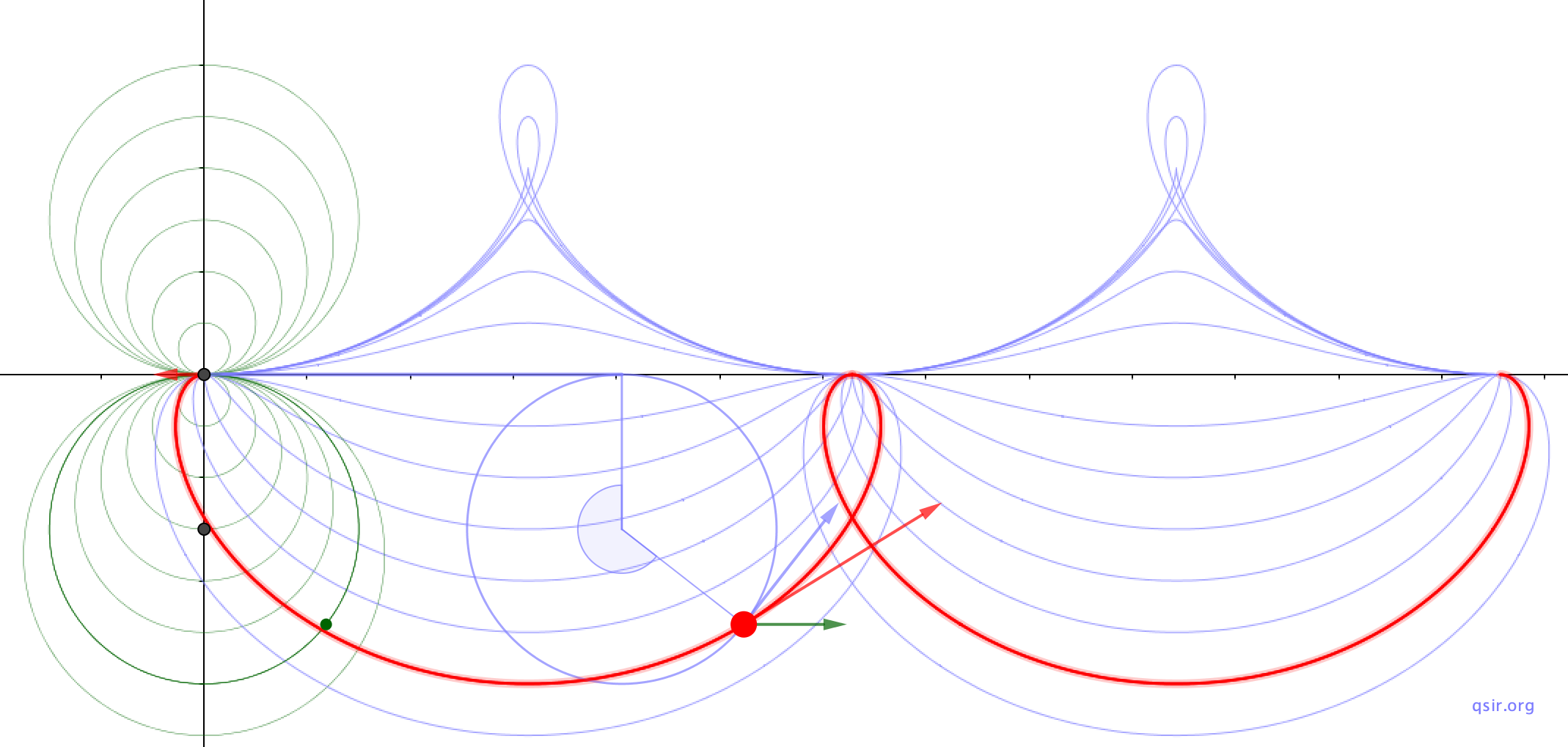
关于带电小球在匀强磁场中的运动，也可以转化为带电粒子在正交匀强电场和匀强磁场中的运动模型。正电q质量m小球在垂直纸面向里的匀强磁场中静止释放，设运动中下落最大高度$h_m$和能获得最大速度$v_m$...
思路1（记得是很多年前，课代表杨洛的思路）
由于只有重力做功（洛伦兹力始终不做功），下落最大高度和最大速度对应；同时，由于是下落最大高度时速度最大，那$v_m$一定是水平的（$v_y=0$）。根据动能定理和水平方向动量定理，可得：
$mgh_m=\frac{1}{2}m{v_m}^2-0$
$\sum Bq v_y \Delta t=mv_m-0$
$Bqh_m=mv_m-0$
联立解得$v_m=2\frac{mg}{qB}$ $h_m=2\frac{m\frac{mg}{qB}}{qB}$

思路2（参考资料上通常给的方法，学生印象深但理解的一般）
静止释放的小球看成是由两个大小相等方向速度的叠加，而特别选取$v_0=\frac{mg}{qB}$，主要的意图是水平向右的速度对应的洛伦兹力能平衡掉重力，这样，带电小球的运动就可以转化为逆时针圆周运动与水平向右匀速直线运动的合成，轨迹是摆线。
至于最大速度和下落最大高度，半个周期时，圆周运动与水平匀速运动速度方向相同，和速度最大$v_m=2\frac{mg}{qB}$，而下落最大高度$h_m=2r$

思路2（建立在思路2）
既然能把运动简化为圆周运动和匀速直线运动的合成，那利用圆周运动在直径上的投影为简谐振动这一点，可以知道带电小球在竖直方向是简谐振动（匀速直线运动不影响竖直方向）。利用简谐振动的最高点和最低点加速度相同，$qBv_m-mg=mg$,得$v_m=2\frac{mg}{qB}$...

思路1的代数法简洁，思路2这里叫几何法的话，很直观，思路3利用二级结论巧算最大速度。这道题目很有趣的地方还在于其初速度的开放性和运动的轨迹的规律性有很好的统一。比如一个周期内的水平跨度，$d=\frac{mg}{qB}T$，$T=\frac{2\pi m}{qB}$，再比如，如果小球的初速度是倾斜的，通过上图应该可以想到，运动的轨迹是水平的$v_0=\frac{mg}{qB}$和小球初速度与$v_0$矢量差为线速度的圆周的叠加，当然回过头看，前面的讨论不过此前提下的是特例。

On this day..

• 教育与美好生活 - 2024
• 写给高三的学弟学妹们 - 2011
• 垮塌 - 2008
• 教师的无奈 - 2005
• 调明灯里的经济学原理 - 2004
• heart to heart - 2003
• 最新的写意图片 - 2003