一道立体模型的摩擦力题

一 10

一道立体模型的摩擦力题

高三|〖苦海泛舟〗 qiusir 2021

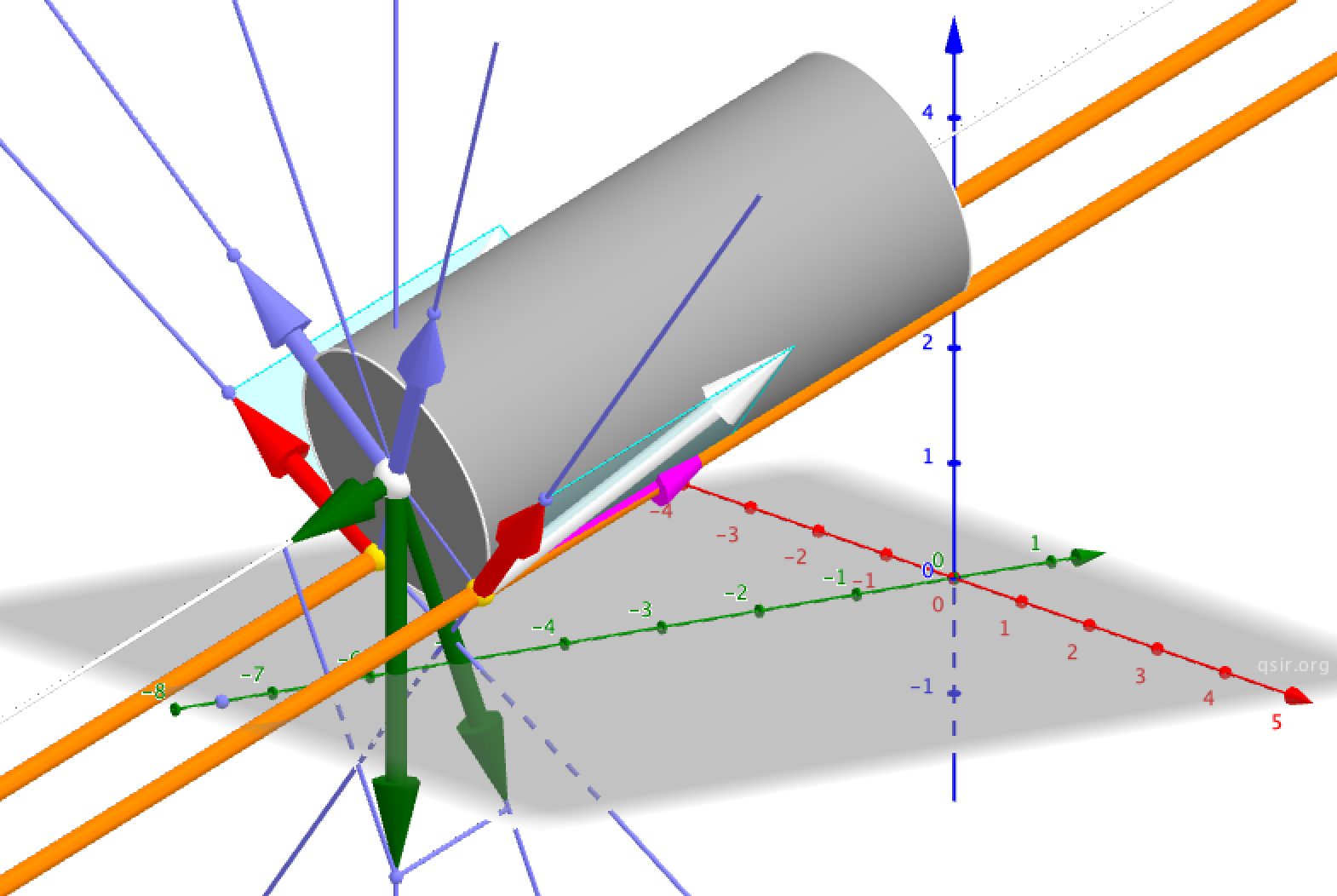
两根长圆柱轴完全相同、轴线在同一面内，且平面与水平面夹角为θ=30°。现将一个大的匀质圆柱体放置两轴之间，且大圆柱体轴线分别与两长圆柱体轴的轴线形成的两个平面夹角为α=60°。试求解以下问题：
一、若大圆柱体恰好静止在轴上，可认为滑动摩擦力与最大静摩擦力相等，则大圆柱体与轴之间的动摩擦因数μ应满足什么条件？
二、已知某种材质的大圆柱体与轴的动摩擦因数μ=2。某一时刻，左侧轴做逆时针转动，同时右侧轴做顺时针转动，两轴转动时边缘处的线速度大小均为v=3m/s，则由于大圆柱体受力发生变化造成其将沿轴下滑，求大圆柱体下滑稳定时的速度。

一：

$2F_Ncos{\frac{\alpha}{2}}=mgcos{\theta}$

$2F_f=mgsin{\theta}$

$F_f\leq\mu F_N$

$\mu\geq0.5$
二：

$2f_1sin{\frac{\alpha}{2}}+2F_Ncos{\frac{\alpha}{2}}=mgcos{\theta}$

$2f_2=mgsin{\theta}$

$\sqrt{{f_1}^2+{f_2}^2}=\mu F_N$

$45\frac{f_2}{f_1}+\frac{f_1}{f_2}=16\sqrt{3}$
得

$\frac{f_2}{f_1}=\frac{\sqrt{3}}{3}$ 或

$\frac{1}{15\sqrt{3}}$

$\frac{v_1}{v_2}=\frac{f_1}{f_2}$

$v_2=\sqrt{3}$ m/s 或

$\frac{\sqrt{3}}{15}$ m/s
对于上面的解，洪诚天同学检测到第二个结果对应的

$F_N$ 是负的。（柱体和轨道有磁性吸引的话？）
如果直接引入两个摩擦力的夹角

$\beta$
代入

$f_1=\mu F_Nsin\beta$

$f_2=\mu F_Ncos\beta$ ，转化成正切计算同样会出现上述问题，

$x^2-16\sqrt{3}x+45=0$ ，得

$\sqrt{3}$ 或

$15\sqrt{3}$ （增根的出现应是平方导致忽视了支持力为正的隐含条件...）
而求解

$cos\beta$ ，会直接检验出增根，

$52x^2+4\sqrt{3}x-45=0$ 得

$\frac{\sqrt{3}}{2}$ 或

$-\frac{15\sqrt{3}}{26}$ （舍）。
洪同学很聪明，特地设定：

$f_1=\mu F_Ncos\varphi$

$f_2=\mu F_Nsin\varphi$ （前面

$\beta$ 的余角），化简后方程相对友善：

$52x^2-24x-1=0$
求解

$sin\varphi=\frac{1}{2}$ 或

$-\frac{1}{26}$ （舍）
所以

$v_2=\sqrt{3}$ m/s

课代表艺博问起五校联考的这道题目，说是学习认真的阿城发现答案有问题，洪同学提供了简洁的做法。吃过晚饭用GeoGebra构造了个立体模型，偷懒用wolframalpha解了方程...
补充一道常规题[?]（150、0.6、480）

On this day..

Comments are closed.