大概读过五六个版本的台湾物理教科书，最近看了日本的，很是感慨。又要被叫秋桑了...
（少儿部学生写的标语，乾坤未定你我皆是黑马，乾坤已定，那就扭转乾坤。）
阿修罗之手、良问之风、名问之森

碰撞后速度，和切面平行方向不变u→u，垂直方向v→ev
不在一条直线上的速度变化量，先于力学的三角形定则2出现
绳的拉力这里叫张力
静摩擦系数$\mu$和动摩擦系数$\mu'$，支持力和摩擦力的合力称抗力
对于弹簧弹力，用图示表明拉伸和压缩相同弹力大小相同；对于等效弹性系数这么好的结论自然不能错过，直列$\frac{1}{k_T}=\frac{1}{k_1}+\frac{1}{k_2}+\cdot\cdot\cdot$，并列...而且在简谐振动部分用到。（可和初中电阻、高中电容串并联等类比，甚至扩大到密度和速度）（用上我的通分子计算更快）
补充了浮力（几何光学中也特别讲了透镜）（浮力和透镜不能简单归为初中知识）
质心($\frac{m_1x_1+m_2x_2+\cdot\cdot\cdot}{m_1+m_2+\cdot\cdot\cdot}$,$\frac{m_1y_1+m_2y_2+\cdot\cdot\cdot}{m_1+m_2+\cdot\cdot\cdot}$)
作用·反作用法则直接提供万有引力和库仑力的范例
研究对象这里是注目物体
拉两个物体和推两个物体，两物体见的作用力$\frac{m_2}{m_1+m_2}F$（分母是没直接受外力的物体质量）
光滑水平面上m以v的初速度在M上表面滑行从相对运动计算（$t=\frac{Mv_0}{(m+M)\mu g}$）（$l=\frac{Mv_0^2}{2(m+M)\mu g}$）（相对静止的时间和相对滑行的距离从动量定理和摩擦生热，出现质量互换和摩擦增加的错觉）
（此部分很妙，重新推到了光滑水平面上叠放的两物体分别具有出速速，前面的表达式同样成立，只是速度替换为相对速度，而且，关于热能问题，可以引入约化质量）
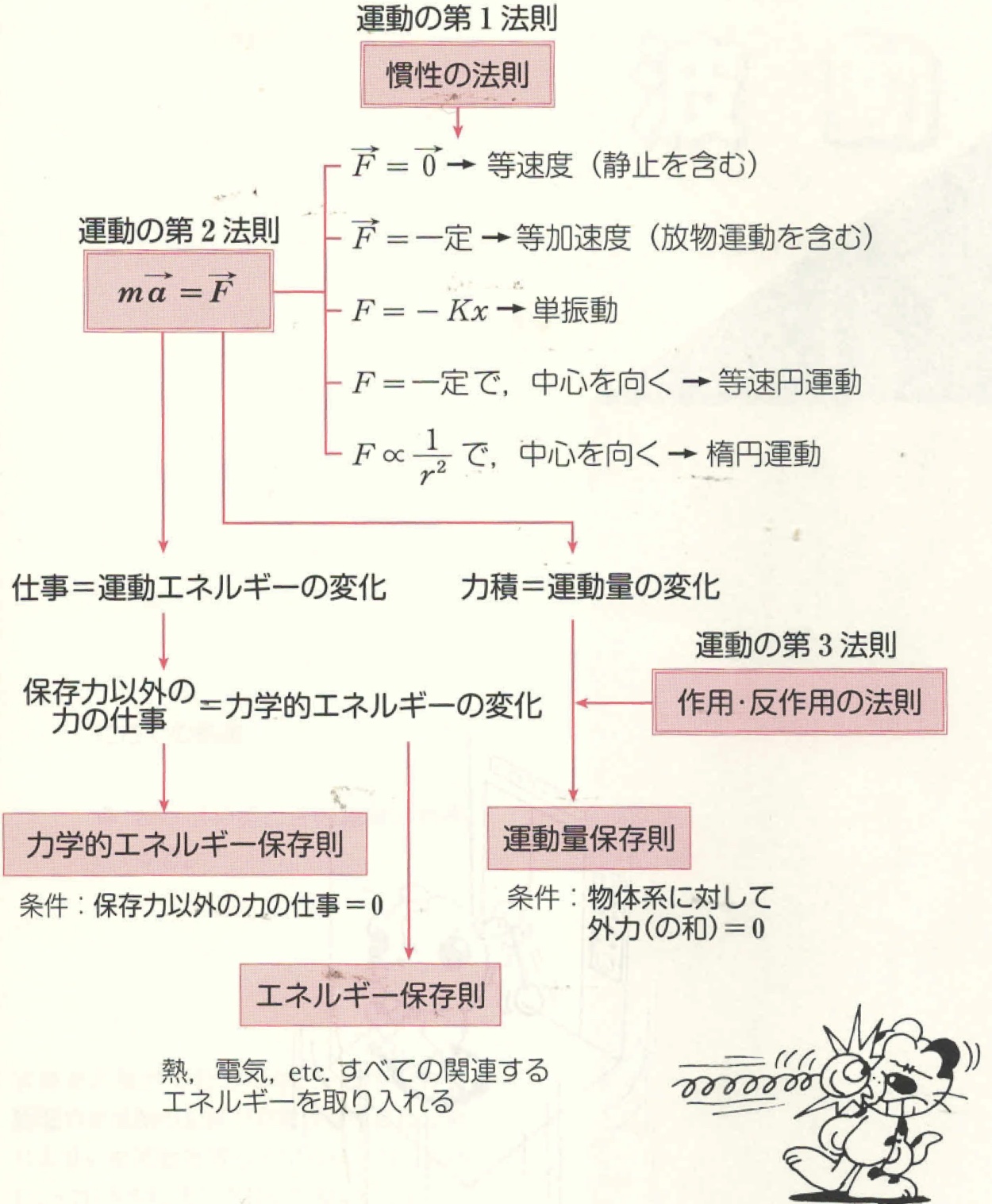
机械能守恒定律---力学能保存则=一定（很好奇这里不用cons.）
运动量/动量 定理直接用向量方式

运动量保存则（巧用平行四边形解释非对心碰撞）（此处应该配自己绘制的图）（力学的平行四边形定则到速度的合成再到动量的分解以及动量定理的运用和牛顿第三定律。）
反発系数在王聪方法上的应用（应该单独整理）
$v_1=\frac{m_1-em_2}{m_1+m_2}v_0$，$v_2=\frac{(1+e)m_1}{m_1+m_2}v_0$（$\Delta E_k=\frac{1}{2}(1-e^2)\frac{m_1m_2}{m_1+m_2}v_0^2$）
（弹簧最大形变量的约化质量（类似等效电阻）求解$\frac{1}{2}kl^2=\frac{1}{2}\frac{m_1m_2}{m_1+m_2}(v_1-v_2)^2$）
（对两物体的完全非弹性碰撞，$m_1v_1+m_2v_2=(m_1+m_2)v$，$v=\frac{m_1v_1+m_2v_2}{m_1+m_2}$，而质心的速度求解，$x_G=\frac{m_1x_1+m_2x_2}{m_1+m_2}$，$v_G=\frac{dx_G}{dt}=\frac{m_1\frac{dx_1}{dt}+m_2\frac{dx_2}{dt}}{m_1+m_2}=\frac{m_1v_1+m_2v_2}{m_1+m_2}$）
惯性力的引入使动力学问题转化为静力学问题（水平加速运动的车上的杯子中水面方向和等效重力垂直），而远心力的引入对有的圆周运动简化。
复原力($\omega=\sqrt{\frac{k}{m}}$，$x=Acos\sqrt{\frac{k}{m}}t$)
$\frac{1}{2}mv^2+mgh+\frac{1}{2}kx^2$=一定 $\frac{1}{2}mv^2+\frac{1}{2}kx^2$=一定 前者x为弹簧形变量，后者x为简谐振动的位移
水平振子有摩擦力的平衡位置跳动（需要再研究）
引力势能、力学能表达式...
粗细均匀的木棒在水中的简谐振动周期$T=2\pi\sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{h}{g}}$（静止时没入的深度，用到浮力替换两个密度的关系，至此周期的专题应该拓展一个）
没有直接引入角动量守恒，用面积定律得出结论 $\Delta S=\frac{1}{2}r(v\Delta t)sin\theta$，$\frac{\Delta S}{\Delta t}=\frac{1}{2}rvsin\theta$（此处圆锥曲线几何性质引入）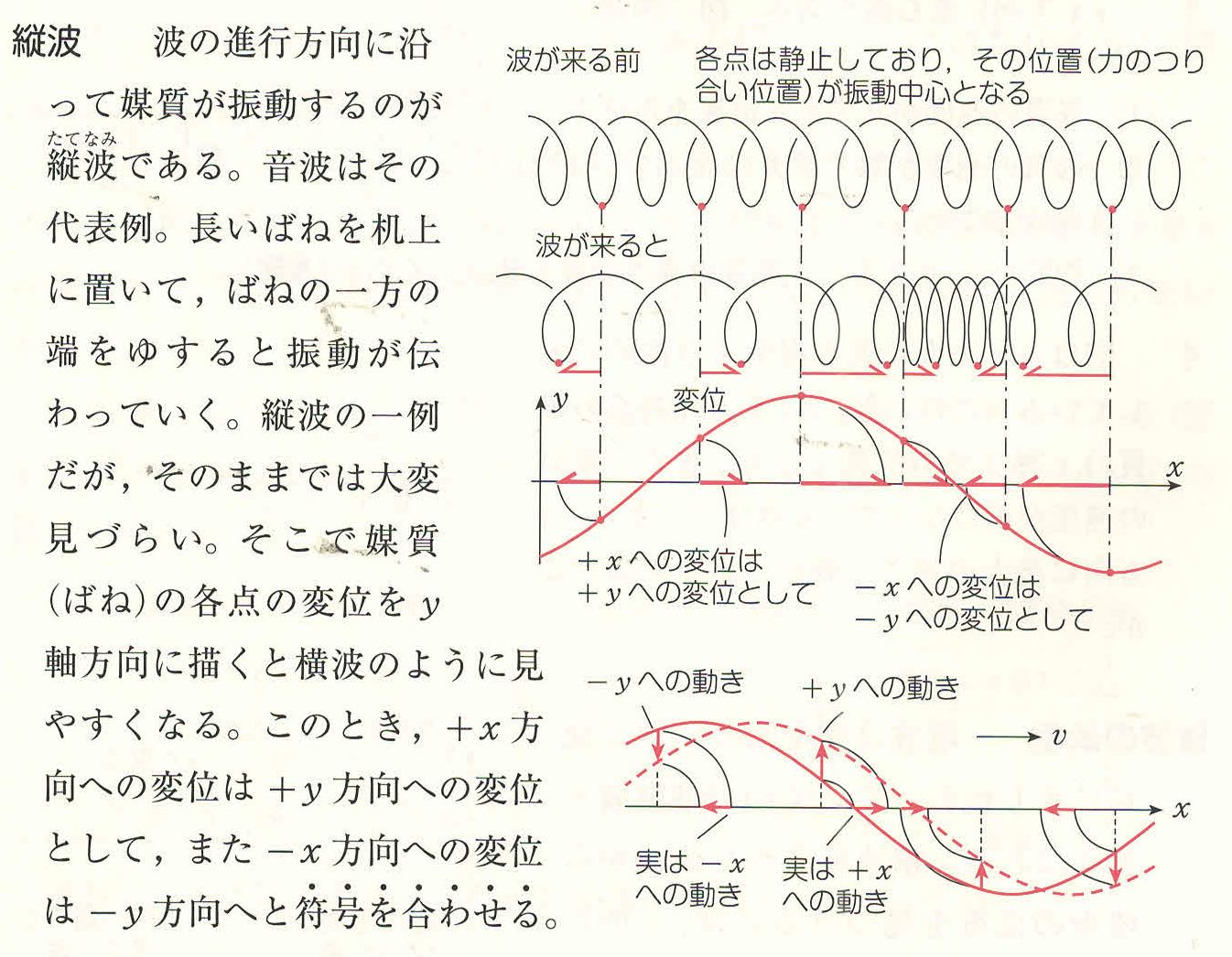

纵波的疏部密部和横波的平衡位置对应的图示（很赞）（两相邻加强点距离$\frac{1}{2}\lambda$）
定长波（驻波）
多普勒效应公式推导
（如果你说的东西给别人讲过多遍，那么这个观点才算是成熟的？）
$f'=\frac{v\pm v_o}{v\mp v_s}f$
f'为观察到的频率；
f为发射源于该介质中的原始发射频率；
v为波在该介质中的行进速度；
$v_o$为观察者相对于介质的移动速度，若接近发射源则前方运算符号为+号，反之则为−号；
$v_s$为发射源相对于介质的移动速度，若接近观察者则前方运算符号为−号，反之则为+号。
冲击波（shock wave）$sin\theta=\frac{V}{v}$
透镜成像的几何结论不应该两不管。

薄膜干涉天文间距$\frac{\lambda}{2}=\Delta x tan\theta$由于小角度，$\Delta x=\frac{\lambda}{2\theta}$
距离差到相位差的转换$\lambda$→$2\pi$ x→$2\pi\frac{x}{\lambda}$
时间差到相位差的转换T→$2\pi$ t→$2\pi\frac{t}{T}$

光程差$2ndcos\theta$

年终回顾
惯性法则（定律）运动第三法则
支持力和摩擦力的合力称抗力
注目物体

光滑水平面上m以v的初速度在M上表面滑行从相对运动计算（$t=\frac{Mv_0}{(m+M)\mu g}$）（$l=\frac{Mv_0^2}{2(m+M)\mu g}$）（相对静止的时间和相对滑行的距离从动量定理和摩擦生热，出现质量互换和摩擦增加的错觉）
（此部分很妙，重新推到了光滑水平面上叠放的两物体分别具有出速速，前面的表达式同样成立，只是速度替换为相对速度，而且，关于热能问题，可以引入约化质量$Q=\frac{1}{2}\frac{Mm}{(m+M)}(v_1+v_2)^2$）
关于恢复系数，类比弹簧，形变量平法和弹性势能成比例，这样的逻辑，损失动能的表达式容易推导一些。

On this day..

• 门风 - 2011
• 教育的三“多” - 2008
• 渺小和瞬间 - 2006
• 什么看什么是什么 - 2005
• “只顾耕耘 不顾收获” - 2004
• 无病呻吟与到此一游 - 2001