一道平抛运动习题的解析
这是一道我很喜欢的运动学综合的习题,图中包含了很多需要分辨的细节,有一定的综合性(匀速、匀加速、直线、曲线),解题方法也很灵活。图中O、A、B、C和D为平抛运动上的点,网格为边长10cm的正方形,已知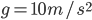 ,根据给定条件求各点的瞬时速度。
,根据给定条件求各点的瞬时速度。

学生一般容易观察到各个点水平距离相同(2各网格),而困惑源自竖直方向间隔竟然是1、2、3和4个网格,通常学生熟练的是竖直方向自由落体运动,相同时间间隔的位移比例应该是1、3、5、7...更大的迷惑是第一个点明明标记的是O,这个也让学生先入为主地断定这是平抛运动的初始点。
困惑处往往就是突破口,线索也就在竖直方向位移的差值,利用匀变速运动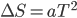 ,
,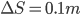 ,水平方向
,水平方向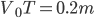 ,求得
,求得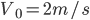 ...找到了乱绳子的头就好办了。
...找到了乱绳子的头就好办了。
就以A点为例,水平速度前面已求得,而对于竖直速度方法很多,更直接的该是利用A点为O和B的中间时刻,利用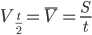 求得
求得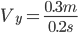 ,A点的合速度
,A点的合速度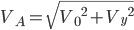 ...同理可以求出其他点的瞬时速度。
...同理可以求出其他点的瞬时速度。

图示中给出O、A、B、C、D各点的速度分解,从运动合成的角度看待各点合速度,以及各点速度增量的图示。矢量运算可以从三角形法则,或是水平匀速相消,而所谓增量仅仅是竖直方向,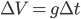 。当然也可以把速度的分解替代成相同时间间隔内位移的矢量差运算,
。当然也可以把速度的分解替代成相同时间间隔内位移的矢量差运算,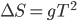 。
。

几何画板自带的过给定五点绘制圆锥曲线的工具,利用这一功能相对容易编制和分析此类平抛运动的问题。下图给出了完整的抛物线图示,可以清晰看到从真正的起始点的竖直距离相同时间内位移的奇数比例的通常情况。
对于平抛运动,一直以来就是通过物理的方法解决数学的问题,想来可以完全可以通过抛物线本身的规律,落实到物理现象上来,充分体现数学的工具性。比如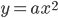 的导数为
的导数为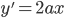 ,
,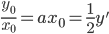 ,如此不难理解平抛运动速度与水平方向夹角的正切为位移与水平夹角正切二倍的事实,也就不难理解相当于从中点初射的等效了。
,如此不难理解平抛运动速度与水平方向夹角的正切为位移与水平夹角正切二倍的事实,也就不难理解相当于从中点初射的等效了。
而对应一般二次函数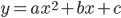 同
同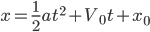 ,二次函数本身就具有
,二次函数本身就具有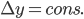 ,对应物理上的
,对应物理上的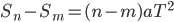 。既然物理上常从物理的角度理解数学的含义,当然也可以在物理上回归到数学本身的规律再赋予物理的内涵。这该是互补的两种方式。
。既然物理上常从物理的角度理解数学的含义,当然也可以在物理上回归到数学本身的规律再赋予物理的内涵。这该是互补的两种方式。
On this day..
- 物理学之美 - 2020
- 从智人到神人 - 2018
- 反弹、乱弹、乱扯、瞎扯 - 2005
- 网络上的生态圈 - 2004
4月 29th, 2010 at 10:54
谢谢,我网站正需要这样的东西
4月 13th, 2022 at 20:46
以前的图被外星人盗走了,这里的应该可以参考:http://www.qiusir.com/?p=18376