和往年相比,今年的高三串讲也推迟了一个月。返校第一周时间相对充足,把要看的书先放一边,趁着更新备考资料把一些繁杂的计算题目也大致过了一遍。关于高三复习,除完成夯实基础的底线,适当也和学生交流一点这个年段应试的上限题目,比如对这道有关“阻力与速度成正比”上抛运动的综合题就有了一个小的想法…
“均匀材料构成的导体圆环,略大于竖直放置的圆柱体。空间存在着垂直于柱体表面的辐射型磁场,圆环所处位置的磁感应强度B,圆环半径为R,质量为m,电阻r,竖直向上的初速度为$$v_0$$,竖直上抛到回到出发点的过程中总时间,$$t_1$$和$$t_2$$、$$q_1$$和$$q_2$$、$$Q_1$$和$$Q_2$$、以及$$v_\frac{h}{2}$$和$$\frac{v_0}{2}$$及$$\frac{\sqrt{2}}{2}v_0$$的大小比较…”
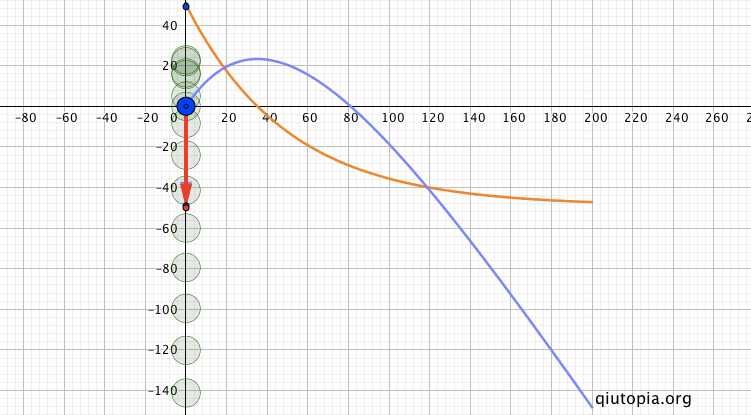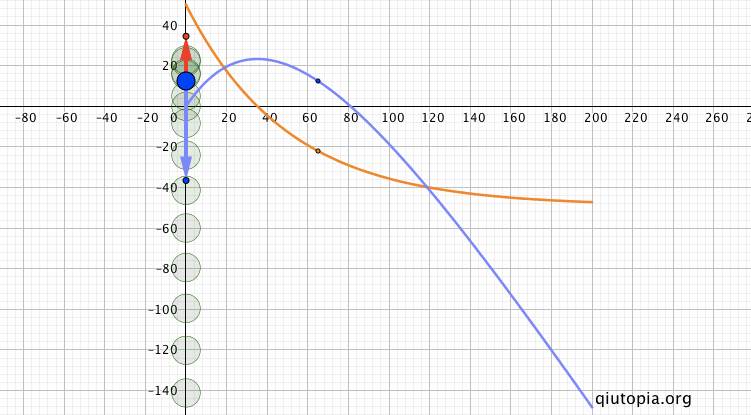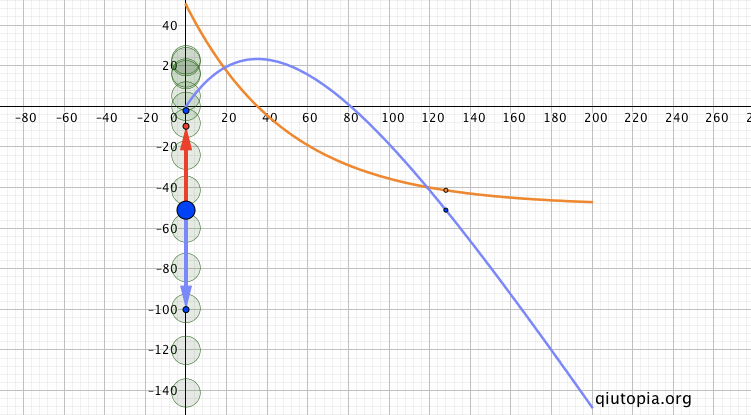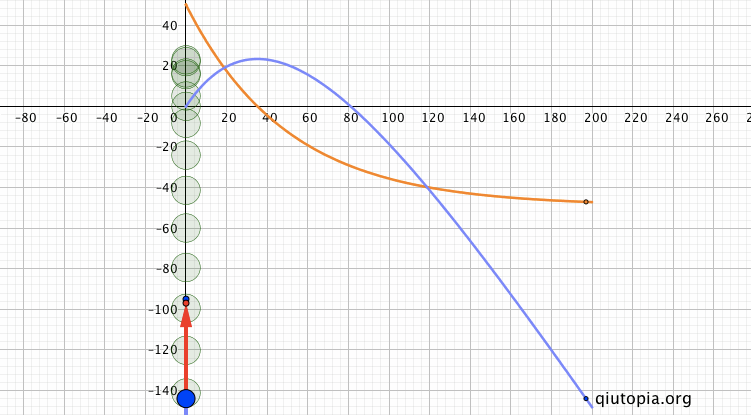
具体考虑这个问题之前,想起之前借助WolframAlpha的帮助构造的一个受到和速度成正比阻力作用下的竖直上抛的模型[?]…
考虑到安培力是$$F_I=\frac{(2\pi{R}B)^2v}{r}$$,上面题目对应受与速度成正比阻力的竖直上抛,那么就可以在之前构造的模型上重新考虑上面一些小问题。比如对$$\frac{v_0}{2}$$和$$\frac{\sqrt{2}}{2}v_0$$,先想到的是匀变速运动的中间时刻和中点的瞬时速度,同时进一步的量化是动量变化一半和动能变化一半的位置,然后分别从动量定理和动能定理考虑…
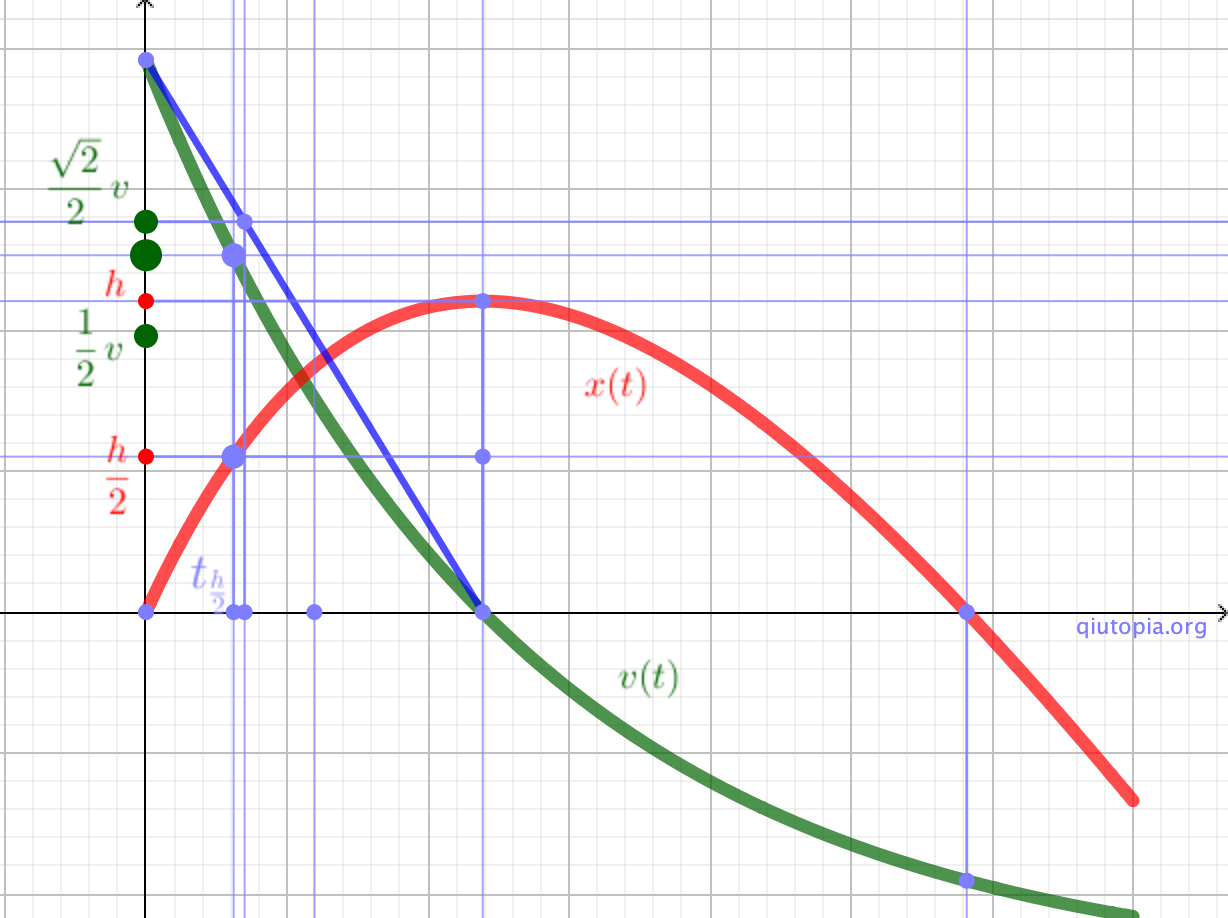
如果仅研究上升过程中点前后的两部分,$$mgt_1+\int{kv}dt$$、$$mgt_2+\int{kv}dt$$,由于前后两部分位移大小相同,阻力冲量相同,但前半部分时间小于后半部分时间,重力的冲量小,那动量变化小,所以有$$v_\frac{h}{2}>\frac{v_0}{2}$$;大概相同的逻辑,$$mg\frac{h}{2}+W_{f1}$$、$$mg\frac{h}{2}+W_{f2}$$,前半部分的阻力大于后半部分,而两部分重力的功相同,总体上前半部分动能损失要大于后半部分,所以$$v_\frac{h}{2}< \frac{\sqrt{2}}{2}v_0$$ 关于总时间,想到阻力与速度成正比,以及来回位移大小相等,上升和下落阻力的冲量为零: $$-mgt-\int{kv}dt+\int{kv}dt=-mv_2-mv_1$$ 而在完成了上面的问题之后,在构造演示图的时候遇到了一个问题,就是$$v_\frac{h}{2}$$对应的时间和作为参照的匀变速运动时间的特殊点有怎样的相对位置?不好说一定在其间啊... 当然这个问题用电脑计算一下倒也快,但最好还是让有能力的学生去运算一下,向同学和欣然很快给出了自己计算,我再用电脑检验和模拟...

我能提出关于$$t_\frac{h}{2}$$和参照时间点的比较的问题就不错了,高级的计算要看年轻人哈哈哈,上面是向同学给出的代数计算,有情趣的同学也可以尝试一下。
P.S.有时间应该更新带电粒子在电容里运动的专题整理,特别是那个对称的偏移问题…
