明天才是教师节，而今天却是收礼物的日子。
单位发现金、组里发牛奶...办公桌上摆着长颈鹿的诚挚，社长送来了桃李，神秘人的留言...现金会花掉，牛奶会喝掉，而真心的祝福会被珍藏。相比物质的慷慨，孩子的真诚更容易触及内心，此时的感动是为人师者的幸福了。

有老师教师节前布置给学生教师相关的开放课题，这可苦了我，中午踢球就有学生希望采访；踢完球又有学生来问卷调查；回到办公室里，又有学生拿着录音机、电脑和相机...有些题目还是很有趣。

问：您认为什么样的学生最有潜力？
答：勤奋的学生最有潜力！
十年的培优经历，见过优秀的学生很多，曾惊讶一些原本不被看好学生的成功，也曾遗憾原本很看好的学生后来的平庸，后来我发现很大一部分是坚持的不同。人的智力差别如同人外在差异的客观，而这些并不决定成功，况且我们更关注那些能够改变的，这就是你自身的努力。坚持本身就是一种能力。

问：您童年的梦想是当老师吗？
答：穷人家孩子的梦想最初多是“出人头地”。
小时候想的最多是“农村包围城市”，哪怕是考上中专到镇上当个收税员就已经很满足了，至少是城市户口了。相反小时候是排斥当老师的，后来上大学学费的“小问题”却改变了一生的足迹。

问：您的学生什么让您最感动？
答：一时想不起来:(哪有那么多惊天动地和刻骨铭心的，真实的生活本来就是平平淡淡。
不能否认人对感动的健忘，最近的事情印象更深。不过不经意间看到学生的进步，就算不是自己的原因也会很高兴。

问：您的老师对您有什么影响？
答：回忆我的老师对我的影响，并不仅是知识逻辑上的指教，相反老师对生活的态度，对事物的观点的教诲让自己更难忘。当然老师当年很多慷慨的善举也会让我感激一生。

问：您怎么看教师是太阳底下最光辉的职业？
答：老师的职业和其他职业一样，伟大也好，平凡也好。而问题的关键是如何对待这个职业，有兴趣地去尽心尽力，执着和责任对任何职业都会赢得尊重。职业的贵贱取决于你对待他的态度。

问：您有机会再选择还会当老师吗？
答：我会更愿意选择尝试其他的行业：）
除非我尝试过所有的行业，要不我怎么知道教师是最适合我的职业呢。而眼下我只能尽力承担自己责任的前提下发展自己的兴趣爱好，尽力喜欢自己的工作，也少让自己遗憾。

问：生活中最重要的是什么？
答：生活中最重要的当然是生活了！
每个人的生活不同，每个人看重的东西自然也不同。

问：学生如何处理和老师的关系？
答：要记住你的老师是帮助你的长辈、是朋友，凡事这样想会好一些。不要奢望你的老师什么都会，而老师最大优势并不仅仅是他的知识，还有的就是他对生活的提前理解，年龄上的一些差距是无法弥补的。

问：您常电脑还有自己的网站，这方面对我们有什么建议？
答：眼下的环境我并不倡导学生上网。不过“每个人都可以站到别人的肩膀上”的网络魅力少有人能抗拒。和网络的虚拟相比，身边的网络---家人、朋友、同学---更重要；和电脑技巧相比，对大多数同学来说，数学、物理等学科知识更重要。

问：您对我们有什么的忠告呢?
答：作最好的你自己！
共性存在，个性彰显，希望你们能够健壮你的身体，发扬你的兴趣，追逐你的梦想，而不是随波逐流。当然还要学会承担你的责任：）

·孔子应该让我们感动

学习向来不缺乏初始的信誓旦旦和对结果的美好期盼，至于学习的过程却往往会被忽略在两者之间。

而解题，对题目结果的渴望强烈得使人从一开始连试题本身都给忽略，往往要经过几次因自以为是而碰壁的经历才能清醒回到最初的条件。
解答题目的最好状态不是展示自己的博学，而是深谙出题者的意图；解题最坏的状态不是不会什么，而是不知道什么不会的不知所云。

学习的最大问题不是什么不会，而是不知道不会什么。明晰了事理是收获，明了了问题也是收获。“提出问题比解决问题更重要”或许也有重视"开化"的考虑。

问题本身的解决并不复杂，或许真正的问题是如何找到问题。

云南行的相册前些天出来了，朋友说和明星画册一样:)很喜欢部长起的名字---七彩云南八月情。闲时信手翻阅，那些静态的图片激活了记忆的碎片，拼凑起过去的画面...

因为顾及球赛又碍于行程，草草浏览了气势磅礴的虎跳峡便匆匆赶回四方街的宾馆...已错过纳西古乐，不想再遗憾丽江古城，起了个大早。
空的小巷，青的石路，红的大门，静的流水，闲的长凳，偶尔的游人愈显古城的舒缓轻柔。
木府门前第一次看到“天雨流芳”的牌匾，品味之余浮想联翩，竟也自信其或有“天降及时雨，流水溢油芳”的揣测。好学的朋友告知那是纳西语“特恩吕芳”的谐音，意思是“读书去吧！”这是自己如何也想不到的，质朴的忠告竟有如此美妙的意境，或许教师职业的缘故，左看右看，竟迟迟不舍离去。对我来说这不能不说是最美的翻译，也远非那“可口可乐”的英译能媲美。
木府里低头见木、玉花园、过街桥、东巴文字、和木传说...都给我留下很深的印象，纳西族妇女“披星戴月”，更让人羡慕纳西族男人们一生只顾琴棋书画、烟酒糖茶的悠闲生活:)

返到四方街时，太阳渐高，游人也多了起来，遥望玉龙，白云萦绕，发觉有静止的异样云彩，阳光下熠熠闪亮...前日雨天，担心错过雪山，相信这次我是看到冰川了。
天雨流芳，书写了放到案头，天雨流芳，铭记下告示后人！

·非魚定未知魚樂
·心无旁骛
·写在临行之前

不出名的人会卖弄名校的出身，不出名的学校会炫耀名人的母校，也有名人和名校的相互攀附，至于出了恶名的人或学校则唯恐避之不及，而不出名的人和不出名的学校或多或少有些彼此的遗憾。
单说“成功”的学生和“有名”的学校，到底谁是谁的运气呢？
常理倾向于优才出自名门，家长多迷信教师而轻视自己，盲信学校而忽视家庭，而成功学生的背后，学校教育表象下似乎隐藏着更大的机密，遗传基因、家庭背景、成长环境...学校仅是其中一小部分。
想起前几天姜平提到的介之推不言禄，他把自己数学上的“发现”谦虚地比喻作“邀天之功”...

窃人之财，犹谓之盗。况贪天之功，以为己力乎？

教育的很多时候就是这样，出了问题则彼此推托，而一有成功的果实又马上争着独享。邀天功的有学校、有老师...
学生的成才离不开学校的教育，同时也是学校的运气；学生的智慧离不开老师的教诲，但也是老师的运气；孩子的茁壮离不开父母的抚养，同样也是父母的运气...
愿我的学生能成为我的运气:)

·你必须找到你所钟爱的东西

自古以来，无论东方还是西方都有天圆地方之说，方圆互化则象征天与地、物质与精神合一。
正方形与圆这两种几何图形在某种条件下一致，比如面积相等或周长相等，我们惯称为“化圆为方”或“化方为圆”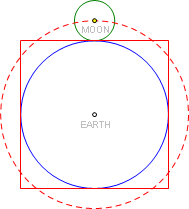，比如“求一正方形，其面积等于一给定圆的面积”就号称是古希腊三大作图问题之一。[公元前５世纪，古希腊人提出了“立方倍积”、“化圆为方”和“三等分角”三大难题。]
非常巧合的是，如果我们用图中间的圆形代表地球，画一个外切的正方形，构造出与“地球”球心为圆心，与外切正方形周长相等的圆，此圆上任意一点与地球相切的圆刚好能够定义出月球的相对大小。
利用NASA WORLDBOOK的数据[月亮的平均半径1,737.4km，地球南北极间距12,713.54km]，得到地球与月球半径比为3.65878，而上图两圆半径比为3.65979，精确度高达99.97%。让人不觉想到希腊“简单是真理标志”的名言。
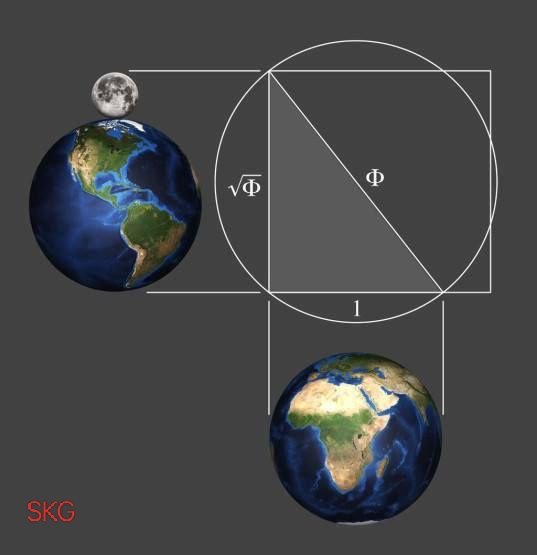
达·芬奇的《维特鲁威人》经常会被科普杂志选用，甚至成了货币上的图案，这里面蕴藏着很多有趣的比例，而其中人与方和圆几何上的关系直接表达了人存天地间的思想，不过其中的圆与正方形的周长并不相等，只能够说是近似。要是当年达·芬奇画成这样就绝了：）
我也尝试着用上面的地球月亮尺度比例整合到维特鲁威人身上，的确有几分神秘的色彩，有时间好好计算一下其它的比例关系。

Update(2018/11/22)

@qiusir:最近和学生讲万有引力定律的部分，找恒星月和朔望月资料时发现十几年前还算过一个有趣的结论：地球与月球极半径比约为3.66，和π/(4-π)非常近似，就说可以通过构造和地球外切正方形等周长的同心圆来近似构造出月球半径的相对大小。
Update(2023/01/15)