
大概两周后有个和老师们的报告会,老师和老师们谈些什么呢?这几天有针对性地读了几本书,又入手了几本,任务驱动还算有效率。下个月会有个和高三学的交流会...
Learning to Teach, Teaching to Learn...

Learning to Teach, Teaching to Learn...

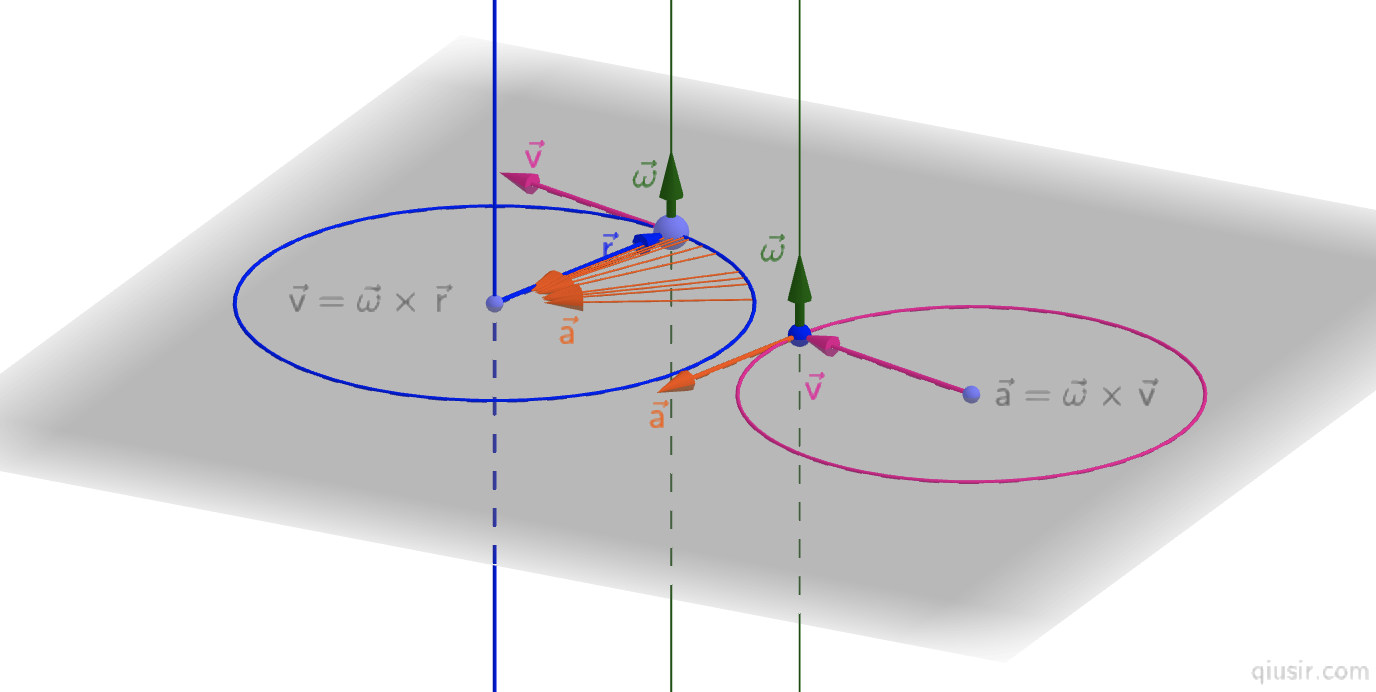
 和线速度v分别和等速圆周运动的线速度v、角速度
和线速度v分别和等速圆周运动的线速度v、角速度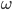 和半径r对应,
和半径r对应, ,
, ,既然
,既然 ,那
,那 。(
。( 是
是 关于时间的求导...)
关于时间的求导...)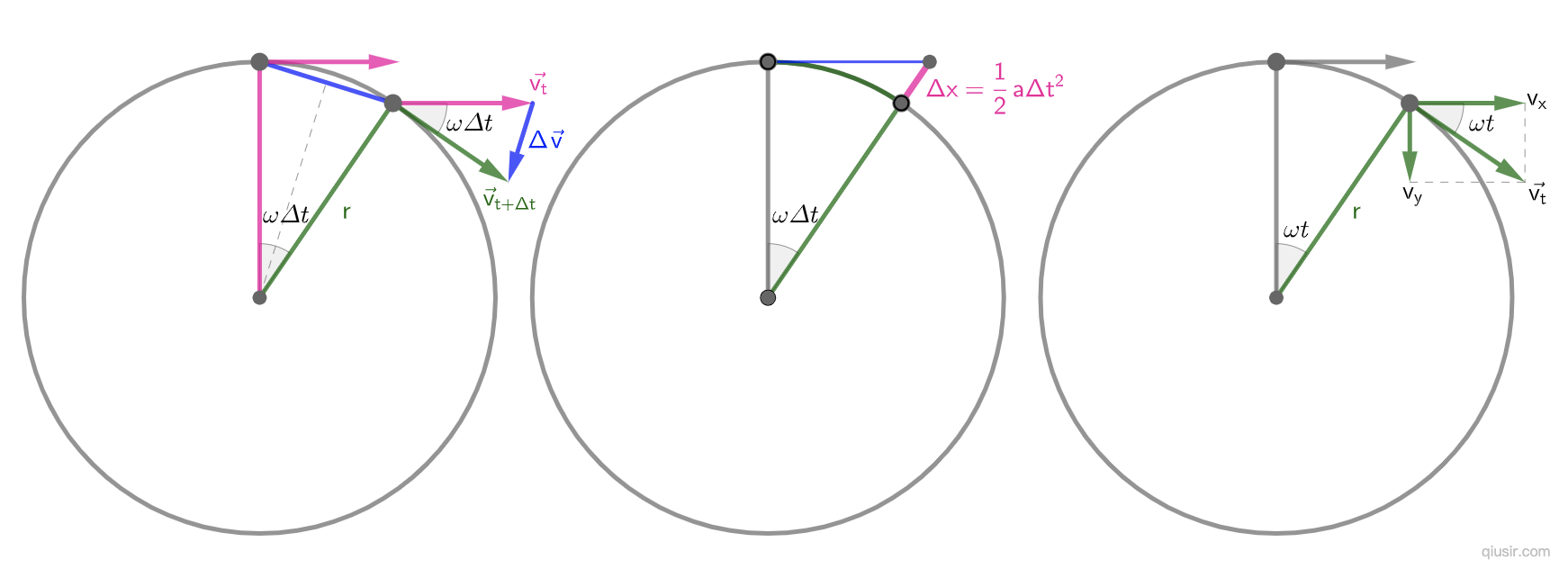
 ,
, ,
, ,
, ;
; 近似弦长,
近似弦长, ,
, ;
; ;
; ,
, ...
...
 ,
, ...
...
和前面不同,另一个思路是从运动叠加的角度推导向心加速度:
⑦这里可以顺便练习一下余弦的近似计算, ,
, ,
, ...
...
⑧同样是运动叠加,用勾股定理近似计算也可, ,简化处理,
,简化处理, ,
, ...
...
⑨对于上面的处理,孙浚豪同学是用移项后平方,高阶无穷小量消项。 ,
, ,
,
⑩用速度矢量的正交分解可关联到简谐振动, ,
, ,分别对时间求导得
,分别对时间求导得 ,
, ,
, ,和通常的极限法分析
,和通常的极限法分析 向心不同,这里可以直接得出加速度方向指向圆心的结论。
向心不同,这里可以直接得出加速度方向指向圆心的结论。
重新整理了这些对应试的意义不大,除了顺便用一下物理中偶尔用到的近似计算,大多数学生只关心结论就可以应付了,但对知识认知的层次是不同的。通常的中学物理教学,不仅对积分和导数的应用过分延后,对向量(矢量)的运算更是脱节,而且意识上的重视明显不够。
美国科学促进会(AAAS)1985年启动2061计划(哈雷彗星2061年会再次光临地球),帮助美国人提高科学、数学及技术素养,“美国历史上最显著的科学教育改革之一” ,号称“终极的科学计划” 。“既然数学对理解自然科学等具有中心重要地位,因而我们再次强调需要把数学与这些学科以综合的方式去教。综合的方法表明,一个现象的数学描述具有阐明和加强的效果。”
直接用加速度是位置矢量关于时间的二阶导数运算不香吗?有时更一般的方法反而会降低认知难度。
 ,
,

 ,
,

更一般:


对于等速圆周运动,



前面是对向心加速度的推导,而对它的理解大多局限在直接应用的层面,在FloatHeadPhysics频道上看到更直观的逻辑:
半径不变速度加倍,相同两个位置的速度变化量同样加倍,而所需要时间则因为速度加倍而减半,所以速度变化量应该是平方倍;同理,速度不变半径加倍,相同位置(角度)的速度变化量不变,而由于弧长加倍速度不变,所需时间加倍,那速度变化率减半。
特地找到杨振宁演讲的原视频截取了关于向心加速度的一段。因为战乱等原因,数学教授的儿子也没有学过高中物理,但似乎不妨碍他日后在物理学上的贡献。而现在的小朋友似乎学的有点多...
另,
发现有用 表示重力的,我觉得这样非常方便,和
表示重力的,我觉得这样非常方便,和 、
、 等表示一致,比用W表示更统一,特别是和万有引力常数G区分开。至于向心加速度,
等表示一致,比用W表示更统一,特别是和万有引力常数G区分开。至于向心加速度, 、
、 都可以,我更习惯弹力用
都可以,我更习惯弹力用 ,而向心力用
,而向心力用 ,都是normal...
,都是normal...
关于是匀速圆周运动还是等速圆周运动,个人更偏向台湾那等速圆周运动的称谓...
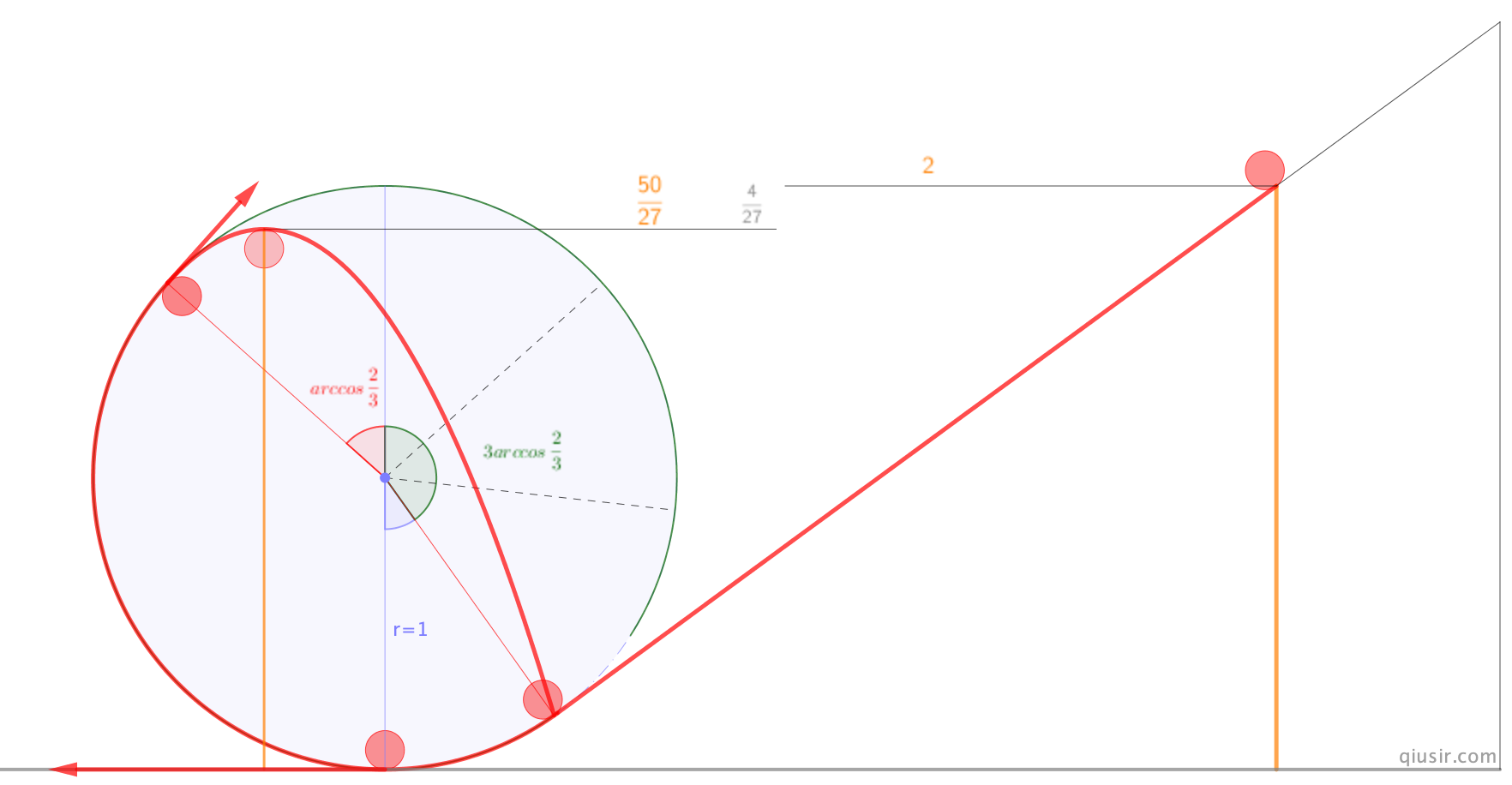
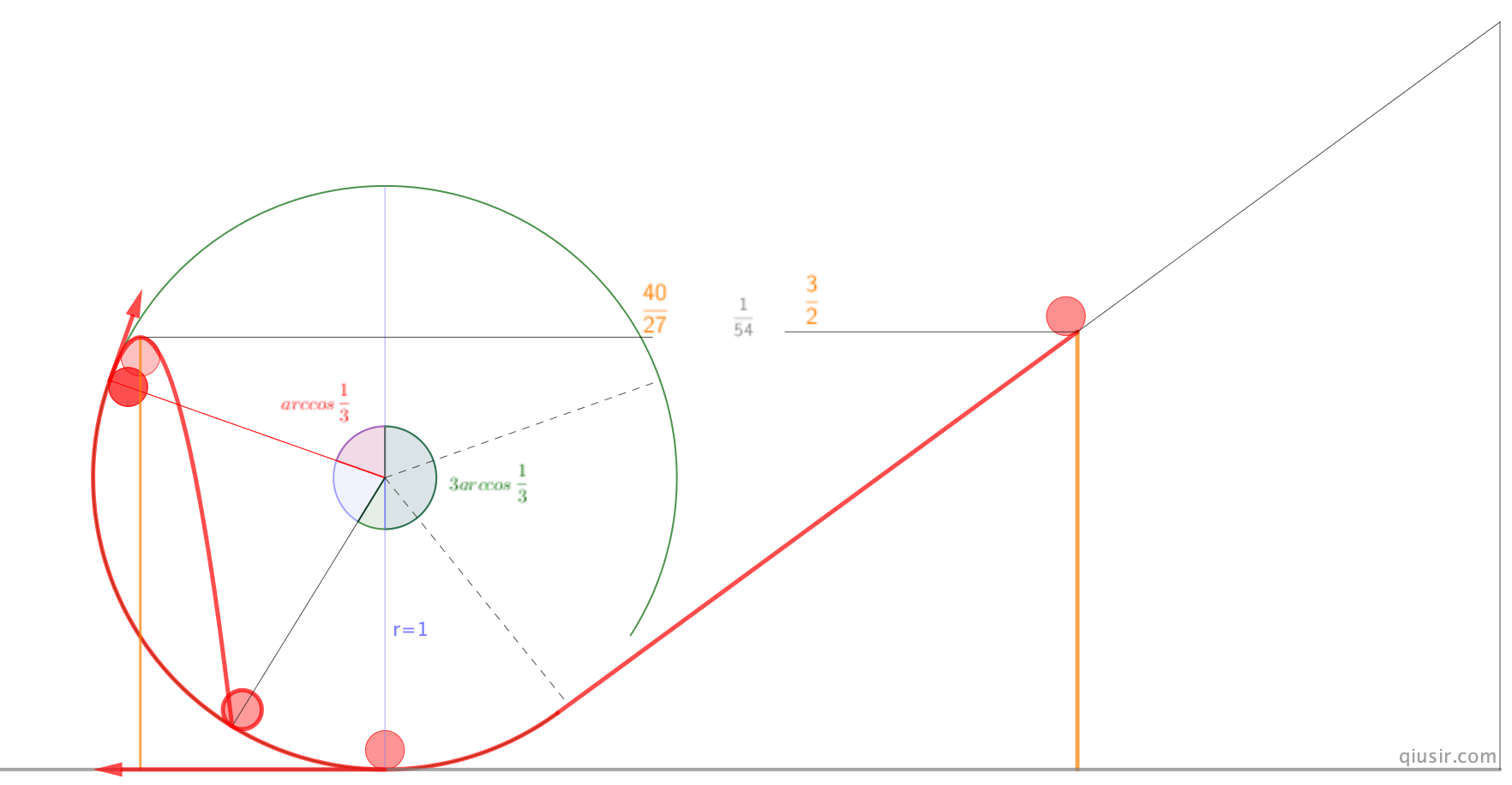
 ,最后为数不多的学生能继续计算,斜上抛的运动学角度或者求出抛体最高点动能再用机械能守恒,计算出
,最后为数不多的学生能继续计算,斜上抛的运动学角度或者求出抛体最高点动能再用机械能守恒,计算出 ...
...

活字印刷术所传播的不是教育,而是狂热的神学;不是人文主义胜利了,而是排斥异己胜利了。
“人生的最高艺术乃是保持住自我。”
“一个头脑理智的人是什么也不会失去的。”时代发生的一切对你是无能为力的,只要你不介入。只要你保持清醒的头脑,时代的疯狂也并不是真正的苦难。
我们使我拥有的唯一的事物和不会失去的事物就是我们“最内在的自我”;他们提醒我们:不要为一切来自外部的、时代的、国家的、政治的强迫行为和义务牺牲自己。因为只有在一切人和一切事面前始终保持自己内心自由的人,才会保持住并扩大人世间的自由呢。
二、从贫民到贵族
成为莎士比亚的老师,成为法国两位国王的顾问,成为法语的光荣...蒙田和这位有犹太血统的母亲在一个屋檐下共同生活了半个世纪...
(蒙恬的爸爸)把有学问的、具有人文主义思想的朋友们请来,和他们商量关于怎样从一开始用人性和上流社会的思想把自己的儿子教育成为一个杰出人才的最佳方法。
没有荆条和眼泪的情况下学会了说最纯粹和最完美的拉丁文。
皮埃尔·德·蒙田:“父亲应该通过唤醒我的自由的意志,通过唤醒我自己的愿望来教会我对知识的鉴别力和对自己职责的鉴别力,而不是强迫;我的心智应该在完全的自由之中非常徐缓地提升,而不应该强硬拔高,不应该有反常的压力。”
“如果人们在早晨突然并强行把孩子从睡眠中唤醒,这对孩子娇嫩的大脑是有害的。”每天用音乐唤醒躺在自己儿童小床里的蒙田。
他身上的那种柔弱和无忧无虑很可能发端于同年的那些岁月。
“老师们总是对着我们的耳朵大声吼叫,好像他们要把知识灌进听筒里似的,而我们要做的事情仅仅是重复他们对我们说过的话。”
“正如植物进水太多就会死去、灯盏的油太多就会熄灭一样,我们的思想活动也会受到过量的学习和过量的教材的影响。”
...教科书以外的文豪们的著作...蒙田一旦陷入如此如醉的随意读书就不能自拔。
对这个很难教育的人的教育表面上是他十三岁时结束。从此以后,蒙田就毕生自己给自己当老师和自己做自己的学生了。
蒙田只有一种成本能的智慧:热爱生命和热爱生命中的自我。
(种牙手术前写这本书的读书笔记,临走还分发了求师得数位学习的纪念证书,种牙回来继续。)
三、载入史册的蒙田
为了较容易地挑起压在他身上的金钱重担,蒙田决定摆脱另一种负担---追求名望。
把自己囿于四周贴满各种格言的环境中,可谓别出心裁。
四、写作十年
“这位思想者最出色的成功之处,是研究了可研究的事物,同事冷静地尊重不可研究的事物。”歌德
蒙田并不是整天都读书,但只要意识到书籍就在身边,他就十分喜悦。
“书籍是人们在人生旅途中能够携带的最好粮食。”
“我的藏书楼是我的王国,我要作为绝地的统治者在这里支配一切。”
如果他沉默不语,书籍就不会打扰他;只有当他向书籍询问时,书籍才会说话。
蒙田和书籍的关系就像对所有事物一样,是一种自由的关系。他既然放弃了一切责任,又何必再给自己增添一种新的责任呢。他说,他年轻时读书时为了炫耀知识,后来读书是为了变得更有智慧,而现在读书只是为了更多的愉快,绝不是为了功利。(多少在第二和第三境界之间。)
书籍应该对他有所启发,而且只有通过启发才会使他受益。
源自内在的原因的结果比外部发生的事件更重要。
谁要以四海为家,其实是他没有家。没有一种风为一个不知驶向哪个港湾的人效力。
蒙田只不过是一个爱反思的人,而不是一个作家。
一个寻求知识的人就应该在知识的海洋中采集知识。
五、寻找自我
(阳了的时候,一方面担心自己死后的财产如何处置,内心很是悲凉;阴了后,又以不会死的样子去积累财富。自己还真是蠢到家了。但,不休止如果不是先天的基因,就是后天的磨砺改变了基因。)
他忘了自己读过的书,记不得读书的日期,回想不起读书时的主要生活情形。一切就像一条河似的流过他的身旁,没有留下任何记忆---没有留下一种确定的信念,没有留下一种坚定的观点,没有留下任何一成不变的记忆。
蒙田如此抱怨自己身上的这个弱点,正是他的优点。他的“不在任何事情上羁绊”这一点,就会迫使他一直往前走。
“我们都是接连不断地重新开始一种新的生活。”他始终是一个不同的人,又始终是同一个人。
“不要大胆地断言什么,不要轻率地否定什么。”
苏格拉底留下的无非是他自己这样一个人物---一个内心向各个方面寻找自我的人。
我们也许最应该感谢米歇尔·德·蒙田身上的那种锲而不舍的寻求的动力---感谢他的浓厚好奇心,感谢他的不好的记性。他之所以成为作家,也要归功于这些。
“我的使命和我的艺术是:创造我自己的生活。”
(可以淡了的人情。)
(都说三代累积出一个贵族,年幼而孤某种程度上算是优势,毕竟书籍某种程度上是更完美的长辈。)
为了享受自己的生活,而且要高尚地享受自己的生活。
谁描述了自己的一生,谁就是为所有的人而活着;谁把自己所处的时代展现出来,谁就是为了各种各样的时代。
“我知道什么呢?”
“我在这里所写的,不是我的说教,而是我为了求知所做的努力;我在这里所写的,不是他人的生活经验,而是我自己的生活经验。”
六、捍卫内心的自由
“天下最了不起的事,就是一个人明白自己是怎样一个人。”
一个人不应该被责任感、激情、虚荣心驱赶得比他原本想要走的更远...一个人不应该成为各种事情的奴隶。一个人应该是自由的。
(如果只有一种频率,我们不仅看不到多彩的世界,听不到动听的旋律。尽管可以不用担心丑陋的画面或是嘈杂的噪音,但也就没有眼睛和耳朵的必要了。)
要把一个多姿多彩的天下纳入种种教条和体系中,而近乎犯罪的错误则是要把别人从他们自己的自由判断中引开---把别人从他自己真正想要做的事情中引开,并且要把他们自己心中不想做的事情强加给他们。只有这些思想专制者们才是毫不尊重自由的人。蒙田最憎恨的是这些思想专制者们的狂热。
马丁·路德曾把墨水瓶向墙壁扔去,因为他认为那是魔鬼。
一个为自己进行思考的人,他尊重人世间的一切自由。
七、意大利之旅
蒙田说,我们所忧虑的事情往往不是事情的原来程度,而是我们不是把事情夸大了就是把事情缩小了。所有的事物都没有自己的分量,认识我们给予了分量。近的事物比远的事物更使我们操心。而且,我们越是在狭小的环境之中鸡毛蒜皮的小事就会使我们闷闷不乐。
蒙田曾一本正经地说,女人拥有比男人更多的更换情人的权利,是呀,难怪有些传记作者怀疑蒙田是不是他的最后几个孩子的父亲。
离开了所有的一切将近两年,唯独没有离开自我。
八、最后的岁月
(教学中的我有很严厉,不少学生怕我;而生活中我可能又太和善了,就连小小的中学生都试图用他人生的浅薄来安慰我灵魂深处溢出的忧虑。)(我的谦虚和我的敏感相克)(床上看完)
译者后记
斯蒂芬·茨威格的《蒙田》则成了他最后的遗言,而他把书稿最初定名《感谢蒙田》。
蒙田坚持说,“我本人就是我的作品的内容。”
谁学会了如何面对死亡,谁就不会再有被奴役的心灵,就能无视一切对自己的束缚和强制。
在赛内卡看来,坚贞的人是知道如何克制自己欲望的人,在人生旅途中步履最轻松,因为这样的人在难以逆料的命运打击下能够像橡树那样屹立于风中而纹丝不动。
“我并不希望由于生活本身需要吃喝,就只顾吃喝,我认为,人应该希冀有双倍的需求,即使是错误也值得原谅。”
“谁教会人如何面对死亡,就是教会人如何生活。”
“人的幸福要等到最后才能说,在他生前和葬礼前,无人有权说他幸福。”
蒙田是洛克[?]的先驱。
“第一位敢于抒发自己内心感受的作家。”
为了能真正读懂蒙田,人不可以太年轻,不可以没有阅历,不可以没有过种种失望。蒙田自由的和不受蛊惑的思考,对像我们这样一代被命运抛到如此动荡不安的世界中的人来说,最有裨益。只有在自己深感震撼的心灵中不得不经历这样一个时代的人---这个时代用战争、暴力和专横的意识形态威胁着每一个人的生活并又威胁着他一生中最宝贵的东西:个人的自由---只有他才知道,在那些乌合之众疯狂的时代里要始终忠于最内在的自我,需要多少勇气、诚实和坚韧。(像是我也经历了两次世界大战。)
(关于蒙田对我的影响,有一个侧面可以印证。曾一度认真思考是不是改名丘田,如果没忘的话,让日语班的学生叫我丘田老师。)
[?]美丽得很贫瘠
[?]蒙田随笔