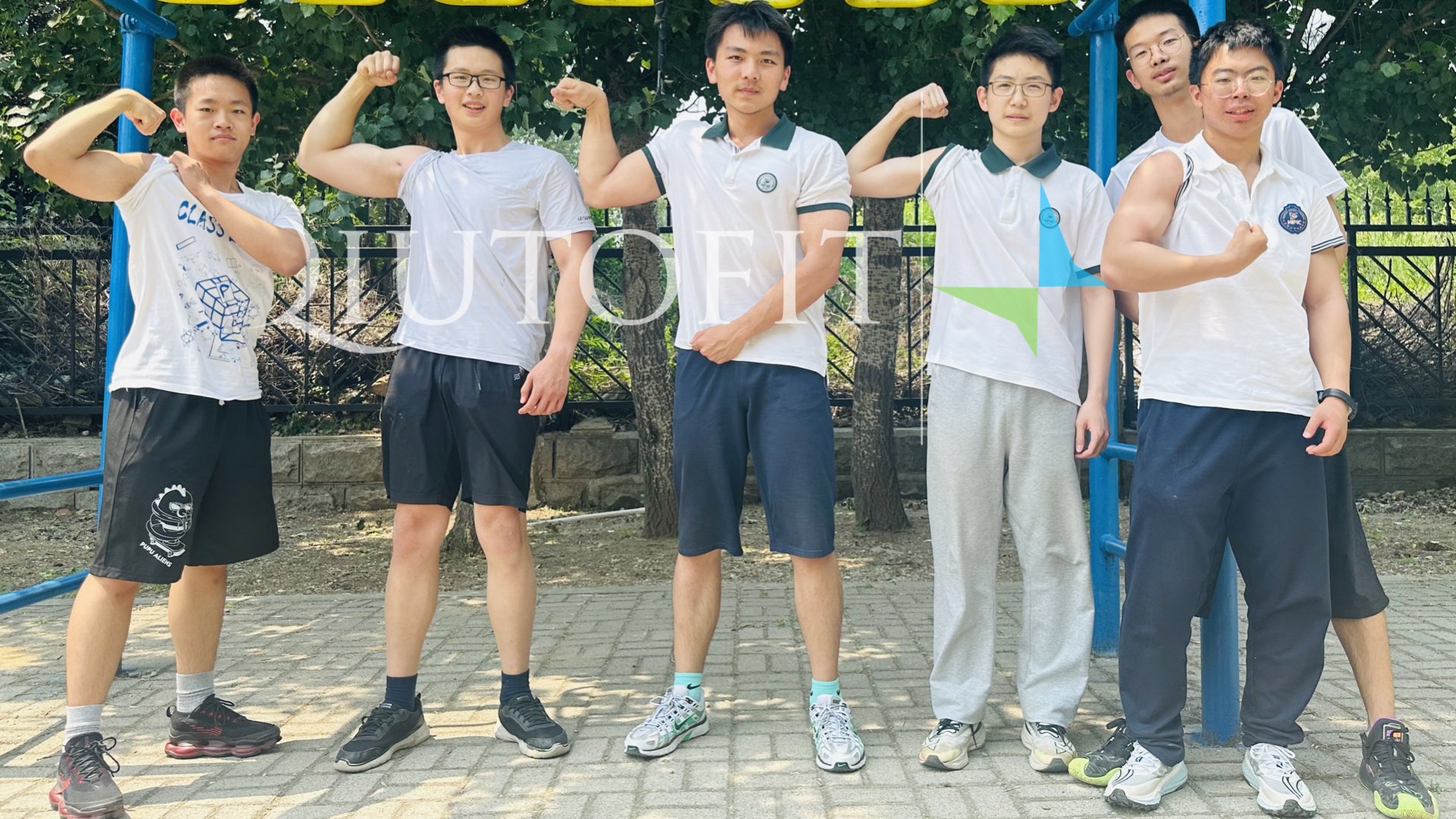swamplands of the soul James hollis new life in dismal places
（从书名上看很适合现在深陷沼泽的我呢，好奇怎么翻译成《中年之路2》解开前半生的束缚，可能第一步太出彩了？）
前言
歌德：真理是神圣的，不是直接就能掌握的东西。唯有在反思中，在例证和象征中，在单一或相关的表象中，我们才能领悟它。它以“令人无法理解的人生”的面目出现，可是我们却无法摆脱想要理解它的欲望。
我们是脆弱的芦苇，也是会思考的芦苇。
若是没有痛苦---它似乎是心理与灵性达到成熟的必要条件---人会停留在无意识的、幼稚的、依赖的状态中。（里尔克说痛苦是一种破茧而出的领悟。）
宗教是为那些害怕下地狱的人准备的，灵性是为那些去过地狱的人准备的。
荣格认为神经症是“一个尚未发现其意义的灵魂所遭受的痛苦”。
“成熟其实并不意味着不会被抛弃，而是我们主动抛弃了一些幻想···如果我们能承担得起独处的焦虑，全新的地平线会铺展开来，而且我们终将学会不依赖他人也能独立存在。”
人类是唯一总想去追寻意义的物种，就好像有某种力量在驱使我们似的。
个体化的目标不是让人沉迷于自恋，一心只想着自己，而是要借由个体，将天地的宏伟意图显化出来···个体化的人物就是追求完整，不是美德，不是纯洁，也不是幸福。

心理治疗的终极目的不在于像考古一样，不断发掘儿时的伤痛，而是逐渐地学习，努力地接纳我们自身的局限，并在此后的余生中努力自行承担起痛苦之重。心理医生的工作并不是提供解脱，让患者摆脱那些造成严重不适的症结，而是要加重不适，教会患者成为成年人，此生第一次去主动面对“独自面对痛苦、被世界抛弃”的感觉。（当老师的何尝不是如此，偶尔治愈、时常关心，总是安慰。）

Continue reading »

里尔克/冯至“
哦，一切何其遥远
而长久地流走。
我相信，这颗星，
我得到它的光芒的时候，
它已经死去了数千年 。
在这广大的夜底下面
我要走出我的心，
我要祷告，
在一切的星中
一定有一颗，
它还活着。
我相信
我知道是哪一颗：
它经久不灭，
它是一切的光的泉源，
它像一座白色的城，
高耸在夜天的顶上 。
”

JQX/进取芯 席明纳第9期（2025.5.21）

1.非惯性参考系中的惯性力：在非惯性参考系中，牛顿三大定律不再成立。为保持牛顿定律的形式，我们引入惯性力：$\vec{F}_{\mathrm{iner}} = -m\vec{a}$。惯性力的方向与参考系加速度的方向相反。例一：两个质量均为m的小物体通过绳子连接，一个悬挂，另一个在一个平台上。求这两个物体的加速度。根据牛顿第二定律：$mg = 2ma$，解得：$a_1 = a_2 = \frac{1}{2}g$。

例二：将上述系统放入一个电梯中，电梯的加速度为向上的$\frac{1}{4}g$，求两个物块的加速度。首先在电梯系中沿绳方向应用牛顿第二定律：$\frac{5}{4}mg = 2ma'$，这里直接引入了方向向下的非惯性力。在转回地面系中，综合电梯本身的加速度可以算出：$a_1 = \sqrt{\left( \frac{1}{4} \right)^2 + \left( \frac{5}{8} \right)^2} \$, $g = \frac{\sqrt{29}}{8}g$，$a_2 = \left( \frac{5}{8} - \frac{1}{4} \right) g = \frac{3}{8}g$。
2. 转动系统中的惯性力：考虑一个人站在转动的圆盘上。在地面参考系中，人受到指向圆心的静摩檫力，这个力提供向心加速度。而在转动参考系中，他是静止的，似乎应该没有向心加速度。如何解释这个矛盾呢，这是因为在非惯性系中我们考虑惯性力的存在。引入一个惯性离心力：$F_{\mbox{iner}} = -m\omega^2 r$，在地面参考系中，摩檫力提供向心力：$f = m\omega^2 r$，在转动系中，惯性离心力与摩檫力平衡，物体处于平衡状态。
邱sir提出一个问题，若把铁块放到转动的砂轮上，铁块是沿切线飞出的，这是典型的圆周运动的问题，为何说静摩檫力是指向圆心的呢？在惯性系看，摩擦力在指向圆心，提供向心力。在非惯性系，物体静止，却似乎受到一个向外甩出的力，这是离心力的表现，用来抵消摩擦力。
重力有反作用力吗，在高中物理中我们常常说重力是万有引力的一个分力，其实指的是在非惯性系统中，物体受到离心力，万有引力，而重力是离心力与万有引力的合力。而离心力是惯性力，它没有施力物体，不符合作用力反作用力的关系。因此作为离心力与万有引力合力的重力，也就没有反作用力。

3.离心势能：离心力沿径向对物体做功，这个功随距离r的增大而增加。因此，我们可以定义一个是势能函数：$U_c=-\int \vec{F}_c\cdot d\vec{r} = -\int m\omega^2 r dr = -\frac{1}{2} m\omega^2 r^2$。由于离心力是在非惯性中假象的虚拟力，离心式能也是存在于非惯性系中的虚拟势能，因此我们也可以理解为离心式能是惯性系与非惯性系中动能之差。
例题：光滑细杆绕竖直轴以角速度$\omega$匀速转动，杆与竖直轴之间的夹角\theta恒定。初始时一个小环静止在杆上的某一高处，之后沿杆下滑。求小环滑到细杆下端时速度大小。

以旋转细杆为参考系，因为这个参考系是非惯性系，因此满足：$E_{\text{grav}} + E_{\text{cf}} + E_{\text{k}} = \text{C}$。因此我们有：$mgh + 0 = \frac{1}{2}mv^2 + \frac{1}{2}m\omega^2 r^2$，其中$r = L \sin\theta$，解得：$v = \sqrt{2gh - \omega^2 L^2 \sin^2\theta}$。该方法求得的速度是在非惯性参考系中得到的，但是由于在细杆底端细杆所在的旋转参考系与地面参考系相对静止，因此两个参考系中小环的速度相同。如果是求小环落到细杆中得某个位置而不是最低端时，则需将速度转化到地面参考系中，这时需要再加上离心势能所对应的“相对动能“。

4.科里奥利力：科里奥利力时发生在旋转参考系（如地球）中的一种惯性力，科氏力是在旋转体系中直线运动的质点，由于惯性相对于旋转体系产生偏移的描述。他是以牛顿力学为基础，由法国科学家科里奥利在1835年提出的假象力。科氏力属于惯性力，不是真实存在的力，而是惯性在非惯性系里的表现。公式定义为：$\vec{F}_{\text{cor}} = -2m\vec{\omega} \times \vec{v}$。地理中的地转偏向力为科里奥利力在地球水平面上的一个分力。它一些通常的体现包括北半球台风逆时针旋转，南半球台风顺时针旋转，子弹在远距离射击时出现偏转，以及地球上的河流在北半球的冲刷右岸，在南半球的冲刷左岸等。
关于科里奥利力以及科里奥利加速度的解释，这里做一些补充。我们可以从两个角度来分析科里奥利力：选一个旋转参考系，一种是沿径向移动一个物体，一种是沿切向移动一个物体。想象一个旋转的辐条，当我们沿径向移动一个物体时，我们发现需要给这个物体一个切向的力。首先，由于半径增大，物体的切向速度增大；其次，它的角动量变大了。但是在旋转参考系中，物体在切向属于平衡状态（在地面参考系中并不是）。那么是什么力来平衡掉来自辐条的切向推力呢？不能是离心力，因为离心力是径向的，我们称这个力为科里奥利力。如果我们沿切向移动一个物体。转盘的角速度为$\omega$，物体距圆心的距离为r，地面系上物体的速度为$\omega_1$，旋转参考系上看物体的速度为$\omega_2$，因此有$\omega_1=\omega_2+\omega$。这个物体受到的向心力为：$F = -m\omega_1^2 \gamma = -m(\omega_2 + \dot{\omega})^2 \gamma= -m\omega_2^2 \gamma - 2m\omega \dot{\omega} \gamma - m\dot{\omega}^2 \gamma$。上式中的第一项为物体在转动参考系中感受到的向心力，即使参考系不旋转，观察者也会知道这个力，第三项是由于参考系旋转感受到的向心力，第二项为科里奥利力。径向和切向的两个力满足同样的规律，因此可以统一表示为：$\vec{F}_\text{cor} = -2m \, \boldsymbol{\omega} \times \vec{v}'$。

JQX|Jin
seminar的一个重要价值在于通过交流和讨论让大家经历一个生成知识的过程。我们深入讨论了非惯性参考系下的三种惯性力：惯性力、离心力和科里奥利力。关于"重力是否有反作用力"这一问题。结合非惯性系中牛顿第三定律不再成立的特点，我们给出了一种较新的解释：重力作为离心力与万有引力的合力，由于离心力是惯性力而非真实的相互作用力，因此重力本身也没有反作用力。

另一个重要收获是对离心势能本质的理解——在特定条件下，它可以视为惯性系与非惯性系中动能的差值。这一认识在解决实际问题时非常有用。例如，在前面的细杆例题中，如果要求小环落到杆的中点时在惯性系下的速度，通过"离心势能是动能差值"这一理解，可以给出很好的计算方法。

但需要指出的是，这一理论在物体有切向速度时不再严格成立，因为会出现额外的交叉项$m\vec{v}_{rel} \cdot (\vec{\omega} \times \vec{r})$。这引出了一个有趣的问题：是否可以定义一个"科里奥利势能"来描述这个交叉项？对于本次讨论的细杆问题，小环相对细杆只有径向速度而无切向速度，所以"动能差值理论"是完全成立的。关于科里奥利势能的物理意义，将在下期seminar中继续进行讨论。

前一阵子中午跑完步还有时间，就去单杠那找找年少的感觉。偶然发现几位很特别的小朋友，别人在踢足球、打篮球或嬉戏打闹，他们在自行练习和切磋，几日观察下来，除了自律，还有知识储备等···想到最近跑步活动开展的不错，是不是也应该鼓励和赞助几位开展个健身的小社团呢，至于名字想到“逆熵社”之类，鉴于先有了qiutorun[?]，那来个qiutofit何尝不可呢。

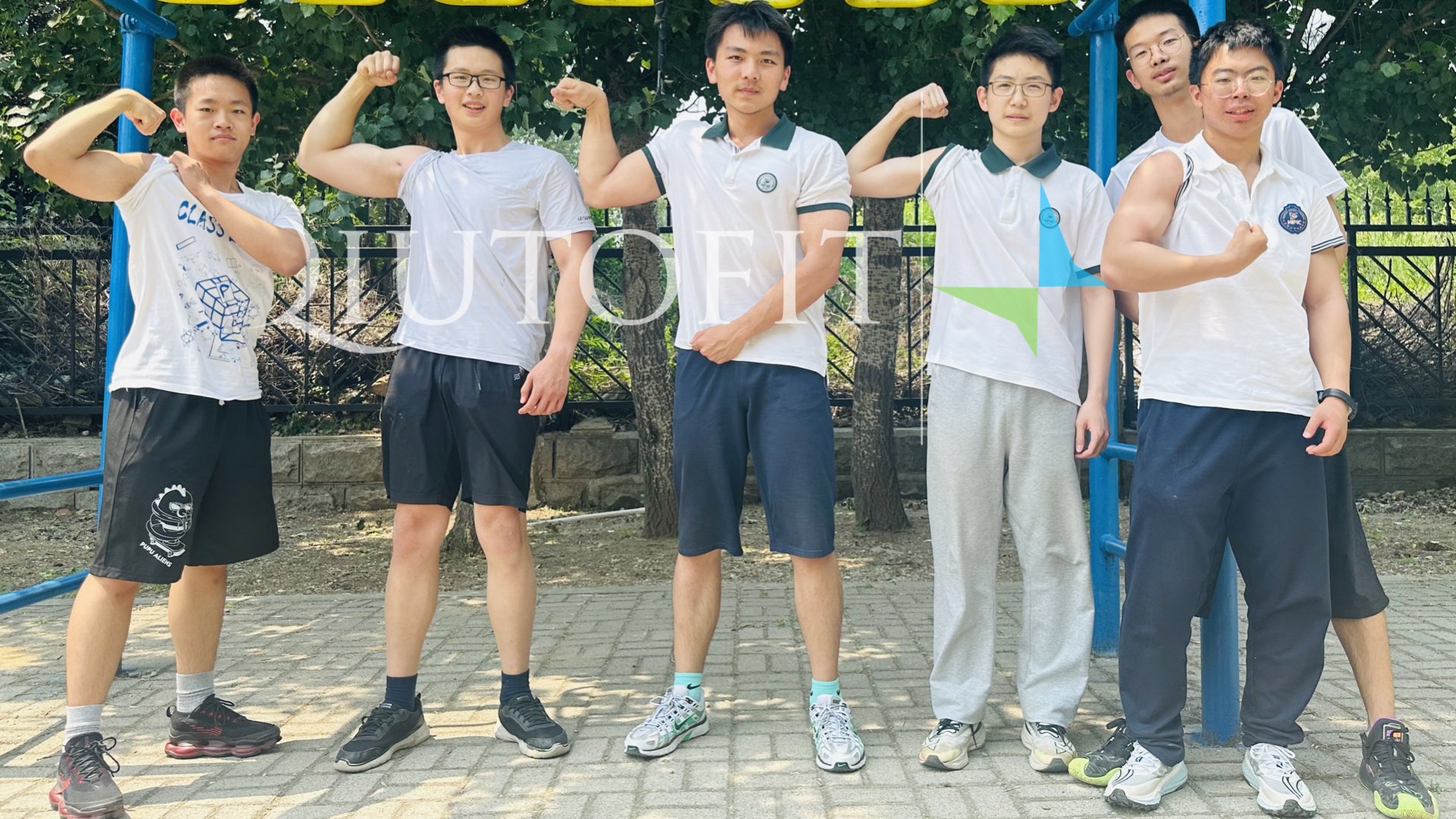
“生命如伙，强健有我。”我喜欢伙伴的“伙”和康健的“健”，因为都有个“亻”的偏旁。等高考结束，月考也结束，相信能有不错的方案。

先预祝高考成功~~~

《反叛的科学家》(The Scientist as Rebel)一代传奇物理大师Freeman Dyson的科学反思
萧秀珊译
一个知识人的诤言
如果把形成共识形容成湖面结冰的话，戴森会不遗余力地在冰面上凿洞。
时间很晚了，然而善恶的选择却在敲着我们的门。
理性的反叛者
二十世纪物理学三大人物，爱因斯坦、霍金和费曼。
狐狸伎俩多，刺猬只懂一种。
科学是人类理性与想象特质的自由发挥。（科学是人类对事物的逐步征服，先是时间与空间，再来是物质那类，然后是自己的身体与其他生物体，最后征服的是自身灵魂中的黑暗与邪恶。）
前言
富兰克林没有受过正规教育，也没有继承大笔财产，但在与欧洲贵族的科学竞赛中，击败了这群博学多闻的贵族们。
富兰克林所展现的反叛是经过深思熟虑的反叛，是由理性与仔细考量所驱动，并非由激情与仇恨所驱使。
（以反叛者的身份去的了伟大的成就，因为他们旨在建立新社会，而不是摧毁旧社会。他也了解传统的价值，他伟大到足以看到事情的两面。）

让胜利者来吧，
当愚昧的堡垒倾倒时，
他们会在墙边找到你的身体！
Mathew Arnold

一、当代科学议题
1、反叛的科学家
他们叫那个倒扣的碗为天空
在那之下被禁锢的我们蠕动着活着与死去
不要举手向它求助
因为它
跟你我一样只会无力打滚
Continue reading »