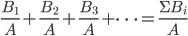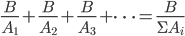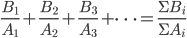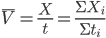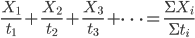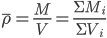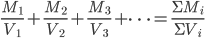三 17
所谓有“理想”的教育者大可以区分为视“理想教育”为个人理想的和践行“现实教育”实现个人理想的,这是“理想的教育”与“教育的理想”的不同。
时下,理想教育的践行者更像是三九天穿裙子,或许是种行为艺术,不过未必美了别人,受冻的却一定是自己;时下,那些固守着传统的,更如草木已换绿装,自己非要裹着那厚厚棉服的,汗流浃背也不舍得脱下一件...时下已是初春,适当增减衣服吧。
偶然看到这样一句话,“一个人要超越他的环境及出身,进步是不够的,非要进化不可,那样大业,岂能人人做到。[?]”这让我联想到本杰明.富兰克林的[?]“有三样东西是及其坚硬的,钢铁、钻石及认识自己。”(There are three things extremely hard: steel, a diamond, and to know one's self. Benjamin Franklin)现在觉得应该补充一句,它们坚硬的程度是递增的,而硬度的极限应该是“改变自己”。这也是传统教育的悖论。
三 15
不知不觉的,这几天过了好几个节,有错过的,有被提前过了的,更有期待的...
@3.12植树节(1979年邓小平提议,每年3月12日为我国的植树节)
也没见有人有去野山坡树木,不过我在教室里树人来着。给学生示范动量缓冲,从讲台上直着腿下来差一点崴了脚,而学生从容地从讲桌上跳下来,冲着关切的我说“我的鞋气垫好”。下次就和他光着脚比...
@3.14圆周率日(MIT提议,2009年美国众议院通过每年3月14日为圆周率日)
有人说要在3月14日1点59分27秒庆祝一下!还有人说要找个阴历的日子纪念一下念祖冲之。抽空也找个地方整个π补上...这一天也是愛因斯坦的生日。
@3.15消费者权益保护日(1962年3月15日美国总统肯尼迪向国会提...)
早上校会听顾同学的演讲才知道3.15的来历...同事抱怨自己家的炉灶、房证...感慨没有时间维权...其实时间不是问题,而国人要维护的岂止消费品的权益呢。
@9.15民主日(2007年11月8日,联大会通过决议每年9月15日举办国际民主日活动)
... ...
@9.10教师节(1985年1月21日,每年的9月10日为我国的教师节)
全国政协委员张树华叫兽建议“教师节”改名“教育节”,理由是“教师节”变味成“送礼节”。如果这样的逻辑也站得住脚的话,那我提议,为加强廉政建设,强烈建议成立一个“官员节”。
@10.4世界动物日(源自19世纪意大利修道士圣·弗朗西斯的倡议)
都说本命年难过,没想到东北虎还真的就在虎年遭了难。以前多少也有点被埋没的牢骚,眼下来看自己还是要好好珍惜呀。稀缺不如东北虎,威猛不如东北虎...百兽之王?沈阳这嘎达就不信邪,不服饿死你小样的...未来我是不敢再憧憬了,眼下的我只有知足万分地先感谢国家、感谢政府了。
... ...
三 04
无意间在
煎蛋上看到
这幅美女戏水图,图中美女甩出的水线轮廓大体是条斐波那契螺旋线(Fibonacci Spiral),墨迹标出的正方形(头发处“-|”属额外标出)就是以斐波那契数列前几项(1, 1, 2)为边长的正方形拼成的,再在每个正方形内面以边长为半径画四分之一圆弧,然后把这些圆弧连起来的线就是斐波那契螺旋线了。
下面给出的是精确示意图(1, 1, 2, 3, 5),这里也给出了更多项数的斐波那契螺旋线。
我上面绘制的图片逆时针旋转90度,可以更方便和上面的水线对照了。图中两个矩形(3,5;5,8;8,13;13,21...)对角线长度的比也很特殊...而说到斐波那契螺旋线(Fibonacci Spiral)居然和
摄影的审美有关系,自然界里的
鹦鹉螺上就隐含着它,还有人为此设计了文化衫呢:)
斐波那契数列(Fibonacci Sequence)在数学上是以递归的方法来定义:F0 = 0 F1 = 1 Fn = Fn - 1 + Fn - 2。前几个斐波那契数是:0,
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946...也正如人类对完美的追求无止境一样,斐波那契数列相邻两项的比例无限趋近黄金分割,所以它也被叫做黄金分割数列,具体细节查阅维基百科,有兴趣还可以参见
一道八百年松鼠难题的文章。
PS.晚上值班,温胜寒问了一个类似地名的一个单词,“Sri Chinmoy”,google翻译出什么斯里兰卡之类的,索性直接搜索一下,原来是位印度籍的国际和谐的大师,还有个很温和的中文名字亲穆仪...喜欢他那句“when the power of love replaces the love of power,man will have a new name:god”“当爱情的力量替代了对权力的热爱,男人就有了一个新的名字:上帝。”
三 02
我们以为以下真理是不言而喻的,这里的每一个人生来都是平等的,他们有一些不可剥夺的权利。其中包括:自由,生活和追求幸福。美国《独立宣言》 起草人:托马斯.杰弗逊
昨晚看了威尔·史密斯父子的励志电影《当幸福来敲门》,算是曲折的剧情,加上父子的绝佳演技,让人不是一般的感动。常理是绝大多数人承受着那些生活上的苦难,却极少分享到电影里那成功的喜悦,生活不是电影。
顺手找来一些印象深刻的台词...其中不少父亲对儿子说的话,有道理,也感人...
You got a dream, you gotta protect it.
如果你有梦想,就要守护它。
People can't do something by themselves; they wanna tell you you can not do it.
当人们做不到一些事情的时候,他们就会对你说你也同样不能。
You want something. Go get it!
有了目标就要全力以赴。
Don't ever let somebody tell you you can't do something, not even me.
别让别人告诉你你成不了才,即使是我也不行。
There is an I in "happiness",There is no Y in "happiness",It's an I.
Y=Why=为什么,I=我。幸福里面没有为什么,只有我。
有一段对白很有趣,说的是加德纳穿着刷墙的衣服从警察局跑去证券公司应聘...
Martin Frohm: What would you say if a man walked in here with no shirt, and I hired him? What would you say?
马丁:如果有个人连衬衫都没穿就跑来参加面试,你会怎么想?
Chris Gardner: He must have had on some really nice pants.
克里斯·加德纳:那他穿的裤子一定十分考究。
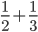 等于多少?学生答
等于多少?学生答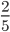 ,一堂课下了也都没有异议...下课后访问学者耐心教上课老师正确的方法...几个月后访问学者恰好又听到那位老师的课,课堂上还是有学生说
,一堂课下了也都没有异议...下课后访问学者耐心教上课老师正确的方法...几个月后访问学者恰好又听到那位老师的课,课堂上还是有学生说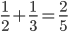 ,下课后访问学者就问上课的老师,“我不是告诉过你这样计算不对吗?”老师很无奈,“我知道,可是大家都喜欢这样计算。”
,下课后访问学者就问上课的老师,“我不是告诉过你这样计算不对吗?”老师很无奈,“我知道,可是大家都喜欢这样计算。”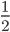 ),下半场罚球三罚一中(
),下半场罚球三罚一中(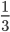 ),整场就是五罚两中(
),整场就是五罚两中(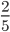 )。”你看这不就是
)。”你看这不就是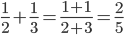 吗,看来人家老美课堂是按照NBA的算法。
吗,看来人家老美课堂是按照NBA的算法。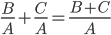 的形式,我们想能不能有
的形式,我们想能不能有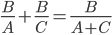 的等式,或是
的等式,或是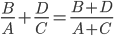 的运算规则呢?(就如罚篮的例子)
的运算规则呢?(就如罚篮的例子)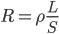 ,假定串联的两个电阻材料(电阻率
,假定串联的两个电阻材料(电阻率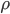 相同,横截面积S相同,电阻的区别仅仅反映在程度L上。
相同,横截面积S相同,电阻的区别仅仅反映在程度L上。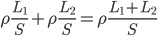 ,所以有
,所以有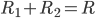 。更一般的情况是,
。更一般的情况是,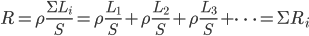 。而对于n个相同的电阻串联,等效电阻
。而对于n个相同的电阻串联,等效电阻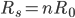 ,这也可以理解为有限的电阻值是由无限的无限小电阻串联累加的,就如1是由2个1/2、3个1/3、4个1/4...n个1/n串联的。
,这也可以理解为有限的电阻值是由无限的无限小电阻串联累加的,就如1是由2个1/2、3个1/3、4个1/4...n个1/n串联的。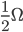 与
与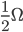 串联,
串联,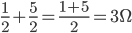 ,也可以考虑成
,也可以考虑成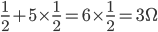 。就是通常的的分数加法运算。
。就是通常的的分数加法运算。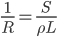 ,假定并联的两个电阻材料(电阻率
,假定并联的两个电阻材料(电阻率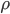 相同,长度L相同)电阻的区别仅仅反映在横截面积S相同。
相同,长度L相同)电阻的区别仅仅反映在横截面积S相同。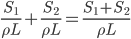 。所以有
。所以有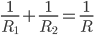 。更一般的情况是,
。更一般的情况是,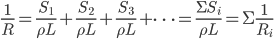 。
。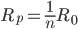 ,这样有限的电阻可以看成是无限多个无限大并联而成。比如1是有2个2、3个3...n个n并联。
,这样有限的电阻可以看成是无限多个无限大并联而成。比如1是有2个2、3个3...n个n并联。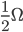 与
与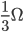 并联等效电阻,方法为
并联等效电阻,方法为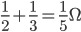 。再如3和6两个电阻并联,
。再如3和6两个电阻并联,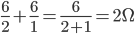 (并联中3相当于2个6)。由此我们可以给出这样的电阻并联公式
(并联中3相当于2个6)。由此我们可以给出这样的电阻并联公式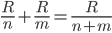 ;
;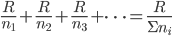
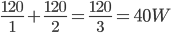 ,再如某热水器单独烧水一壶水的时间为30分钟,另一热水器单独烧开同一壶水的时间为15分钟,并联两热水器后共同烧水的时间计算可以按照
,再如某热水器单独烧水一壶水的时间为30分钟,另一热水器单独烧开同一壶水的时间为15分钟,并联两热水器后共同烧水的时间计算可以按照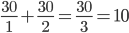 分钟。具体的可以参考以前的一篇电功率计算的一种方法。
分钟。具体的可以参考以前的一篇电功率计算的一种方法。;
;