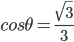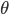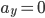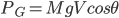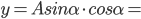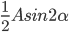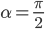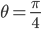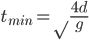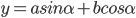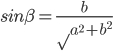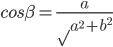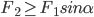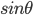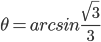很多年前听过这样一个故事:说大陆的一位访问学者一次去一所美国中学听课,数学课上老师问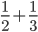 等于多少?学生答
等于多少?学生答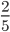 ,一堂课下了也都没有异议...下课后访问学者耐心教上课老师正确的方法...几个月后访问学者恰好又听到那位老师的课,课堂上还是有学生说
,一堂课下了也都没有异议...下课后访问学者耐心教上课老师正确的方法...几个月后访问学者恰好又听到那位老师的课,课堂上还是有学生说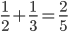 ,下课后访问学者就问上课的老师,“我不是告诉过你这样计算不对吗?”老师很无奈,“我知道,可是大家都喜欢这样计算。”
,下课后访问学者就问上课的老师,“我不是告诉过你这样计算不对吗?”老师很无奈,“我知道,可是大家都喜欢这样计算。”
这原本是“专家”用来讽刺美国课堂上所谓的民主,也反衬我们“领先国际”的基础教育...但换个角度看,难道分数的加法一定要通分吗?我就听过这样的范例,“说一场比赛中,姚明上半场罚球两罚一中(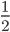 ),下半场罚球三罚一中(
),下半场罚球三罚一中(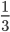 ),整场就是五罚两中(
),整场就是五罚两中(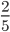 )。”你看这不就是
)。”你看这不就是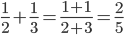 吗,看来人家老美课堂是按照NBA的算法。
吗,看来人家老美课堂是按照NBA的算法。
数学上分数加法的规则是分母相同的,分母不变分子相加,分母不同的要先通分母后再相加。而由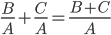 的形式,我们想能不能有
的形式,我们想能不能有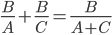 的等式,或是
的等式,或是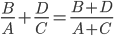 的运算规则呢?(就如罚篮的例子)
的运算规则呢?(就如罚篮的例子)
或者是否可以给出更一般形式的分数运算规则:
1、
2、
3、
就如矢量的运算满足平行四边形法则一样,其实有一些物理量的计算就可以按照上面的泛加法规则进行,我戏称之为分数加法的自然法则。比如物理中串并联电路等效电阻的计算,题目尽管相对容易,而计算的速度和准确程度往往并不理想。这里按照上面的思路给出另外的一种视角,或许可以解决这样的困惑。
电阻的串联,满足规则1。
由电阻的定义式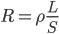 ,假定串联的两个电阻材料(电阻率
,假定串联的两个电阻材料(电阻率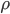 相同,横截面积S相同,电阻的区别仅仅反映在程度L上。
相同,横截面积S相同,电阻的区别仅仅反映在程度L上。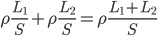 ,所以有
,所以有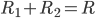 。更一般的情况是,
。更一般的情况是,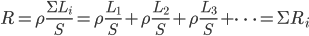 。而对于n个相同的电阻串联,等效电阻
。而对于n个相同的电阻串联,等效电阻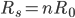 ,这也可以理解为有限的电阻值是由无限的无限小电阻串联累加的,就如1是由2个1/2、3个1/3、4个1/4...n个1/n串联的。
,这也可以理解为有限的电阻值是由无限的无限小电阻串联累加的,就如1是由2个1/2、3个1/3、4个1/4...n个1/n串联的。
串联电路等效电阻的计算相对容易,比如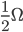 与
与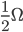 串联,
串联,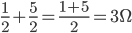 ,也可以考虑成
,也可以考虑成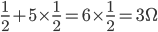 。就是通常的的分数加法运算。
。就是通常的的分数加法运算。
电阻并联的运算,满足规则2。
由电阻定义公式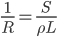 ,假定并联的两个电阻材料(电阻率
,假定并联的两个电阻材料(电阻率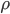 相同,长度L相同)电阻的区别仅仅反映在横截面积S相同。
相同,长度L相同)电阻的区别仅仅反映在横截面积S相同。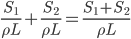 。所以有
。所以有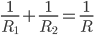 。更一般的情况是,
。更一般的情况是,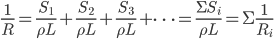 。
。
而对于n个相同的电阻并联,等效电阻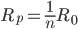 ,这样有限的电阻可以看成是无限多个无限大并联而成。比如1是有2个2、3个3...n个n并联。
,这样有限的电阻可以看成是无限多个无限大并联而成。比如1是有2个2、3个3...n个n并联。
比如计算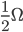 与
与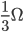 并联等效电阻,方法为
并联等效电阻,方法为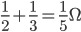 。再如3和6两个电阻并联,
。再如3和6两个电阻并联,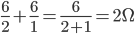 (并联中3相当于2个6)。由此我们可以给出这样的电阻并联公式
(并联中3相当于2个6)。由此我们可以给出这样的电阻并联公式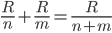 ;
;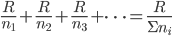
在串联电路中6等于2个3,3与6串联是(2+1)个3为9;而并联电路中,3相当于2个6,3与3并联,(1+2)个6并联为2。也就是说电阻串联需要分母通分,电阻并联需要的是分子通分。电路中1是由无穷多个无穷小电阻串联,1也是由无穷多个无穷大电阻并联。一个1包含无穷多个无穷小,可以看成无穷多个无穷大...很哲学呀。
对于规则2,不仅电阻的并联,等额定电压电器串联后总电功率的运算和加热时间的运算等都满足。比如(220V,120W)的灯与(220V,60W)的灯串联在220V的电路中,总功率的计算就满足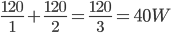 ,再如某热水器单独烧水一壶水的时间为30分钟,另一热水器单独烧开同一壶水的时间为15分钟,并联两热水器后共同烧水的时间计算可以按照
,再如某热水器单独烧水一壶水的时间为30分钟,另一热水器单独烧开同一壶水的时间为15分钟,并联两热水器后共同烧水的时间计算可以按照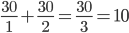 分钟。具体的可以参考以前的一篇电功率计算的一种方法。
分钟。具体的可以参考以前的一篇电功率计算的一种方法。
那什么物理量的运算会满足规则3呢?想来平均速度的运算和平均密度的运算就满足。
;
;
以上的方法耐心体会联系,如果使用恰当可以大大提高计算的速度,不过等式仅仅是物理结果上的等,考试的计算过程课不要直接用呀。
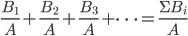
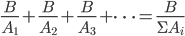
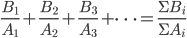
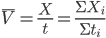
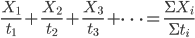
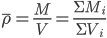
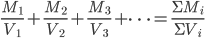
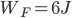
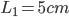
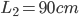
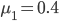
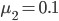
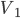
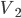
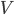
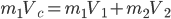
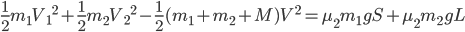
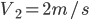
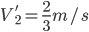
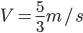
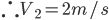
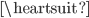
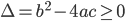
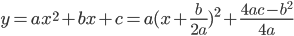
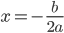
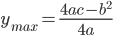
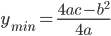
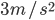
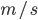
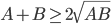
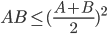
![A+B+C\geq3\sqrt[3]{ABC}](http://www.qiusir.com/wp-content/plugins/latex/cache/tex_571f356391246c2adb723fe4687d811b.gif)