



里尔克/冯至“
哦,一切何其遥远
而长久地流走。
我相信,这颗星,
我得到它的光芒的时候,
它已经死去了数千年 。
在这广大的夜底下面
我要走出我的心,
我要祷告,
在一切的星中
一定有一颗,
它还活着。
我相信
我知道是哪一颗:
它经久不灭,
它是一切的光的泉源,
它像一座白色的城,
高耸在夜天的顶上 。
”
JQX/进取芯 席明纳第9期(2025.5.21)

1.非惯性参考系中的惯性力:在非惯性参考系中,牛顿三大定律不再成立。为保持牛顿定律的形式,我们引入惯性力: 。惯性力的方向与参考系加速度的方向相反。例一:两个质量均为m的小物体通过绳子连接,一个悬挂,另一个在一个平台上。求这两个物体的加速度。根据牛顿第二定律:
。惯性力的方向与参考系加速度的方向相反。例一:两个质量均为m的小物体通过绳子连接,一个悬挂,另一个在一个平台上。求这两个物体的加速度。根据牛顿第二定律: ,解得:
,解得: 。
。

例二:将上述系统放入一个电梯中,电梯的加速度为向上的 ,求两个物块的加速度。首先在电梯系中沿绳方向应用牛顿第二定律:
,求两个物块的加速度。首先在电梯系中沿绳方向应用牛顿第二定律: ,这里直接引入了方向向下的非惯性力。在转回地面系中,综合电梯本身的加速度可以算出:
,这里直接引入了方向向下的非惯性力。在转回地面系中,综合电梯本身的加速度可以算出: ,
,  ,
, 。
。
2. 转动系统中的惯性力:考虑一个人站在转动的圆盘上。在地面参考系中,人受到指向圆心的静摩檫力,这个力提供向心加速度。而在转动参考系中,他是静止的,似乎应该没有向心加速度。如何解释这个矛盾呢,这是因为在非惯性系中我们考虑惯性力的存在。引入一个惯性离心力: ,在地面参考系中,摩檫力提供向心力:
,在地面参考系中,摩檫力提供向心力: ,在转动系中,惯性离心力与摩檫力平衡,物体处于平衡状态。
,在转动系中,惯性离心力与摩檫力平衡,物体处于平衡状态。
邱sir提出一个问题,若把铁块放到转动的砂轮上,铁块是沿切线飞出的,这是典型的圆周运动的问题,为何说静摩檫力是指向圆心的呢?在惯性系看,摩擦力在指向圆心,提供向心力。在非惯性系,物体静止,却似乎受到一个向外甩出的力,这是离心力的表现,用来抵消摩擦力。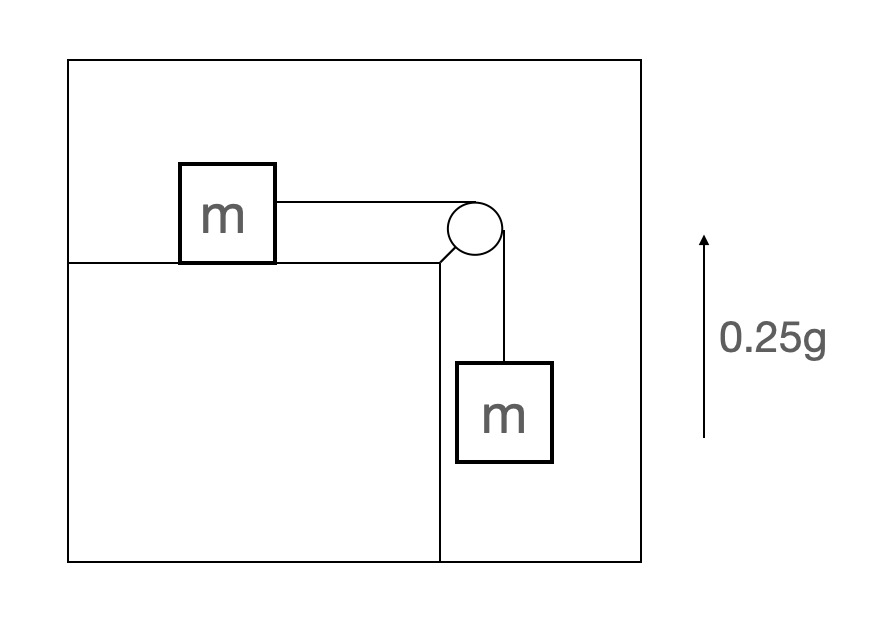
重力有反作用力吗,在高中物理中我们常常说重力是万有引力的一个分力,其实指的是在非惯性系统中,物体受到离心力,万有引力,而重力是离心力与万有引力的合力。而离心力是惯性力,它没有施力物体,不符合作用力反作用力的关系。因此作为离心力与万有引力合力的重力,也就没有反作用力。

3.离心势能:离心力沿径向对物体做功,这个功随距离r的增大而增加。因此,我们可以定义一个是势能函数: 。由于离心力是在非惯性中假象的虚拟力,离心式能也是存在于非惯性系中的虚拟势能,因此我们也可以理解为离心式能是惯性系与非惯性系中动能之差。
。由于离心力是在非惯性中假象的虚拟力,离心式能也是存在于非惯性系中的虚拟势能,因此我们也可以理解为离心式能是惯性系与非惯性系中动能之差。
例题:光滑细杆绕竖直轴以角速度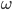 匀速转动,杆与竖直轴之间的夹角\theta恒定。初始时一个小环静止在杆上的某一高处,之后沿杆下滑。求小环滑到细杆下端时速度大小。
匀速转动,杆与竖直轴之间的夹角\theta恒定。初始时一个小环静止在杆上的某一高处,之后沿杆下滑。求小环滑到细杆下端时速度大小。
以旋转细杆为参考系,因为这个参考系是非惯性系,因此满足: 。因此我们有:
。因此我们有: ,其中
,其中 ,解得:
,解得: 。该方法求得的速度是在非惯性参考系中得到的,但是由于在细杆底端细杆所在的旋转参考系与地面参考系相对静止,因此两个参考系中小环的速度相同。如果是求小环落到细杆中得某个位置而不是最低端时,则需将速度转化到地面参考系中,这时需要再加上离心势能所对应的“相对动能“。
。该方法求得的速度是在非惯性参考系中得到的,但是由于在细杆底端细杆所在的旋转参考系与地面参考系相对静止,因此两个参考系中小环的速度相同。如果是求小环落到细杆中得某个位置而不是最低端时,则需将速度转化到地面参考系中,这时需要再加上离心势能所对应的“相对动能“。

4.科里奥利力:科里奥利力时发生在旋转参考系(如地球)中的一种惯性力,科氏力是在旋转体系中直线运动的质点,由于惯性相对于旋转体系产生偏移的描述。他是以牛顿力学为基础,由法国科学家科里奥利在1835年提出的假象力。科氏力属于惯性力,不是真实存在的力,而是惯性在非惯性系里的表现。公式定义为: 。地理中的地转偏向力为科里奥利力在地球水平面上的一个分力。它一些通常的体现包括北半球台风逆时针旋转,南半球台风顺时针旋转,子弹在远距离射击时出现偏转,以及地球上的河流在北半球的冲刷右岸,在南半球的冲刷左岸等。
。地理中的地转偏向力为科里奥利力在地球水平面上的一个分力。它一些通常的体现包括北半球台风逆时针旋转,南半球台风顺时针旋转,子弹在远距离射击时出现偏转,以及地球上的河流在北半球的冲刷右岸,在南半球的冲刷左岸等。
关于科里奥利力以及科里奥利加速度的解释,这里做一些补充。我们可以从两个角度来分析科里奥利力:选一个旋转参考系,一种是沿径向移动一个物体,一种是沿切向移动一个物体。想象一个旋转的辐条,当我们沿径向移动一个物体时,我们发现需要给这个物体一个切向的力。首先,由于半径增大,物体的切向速度增大;其次,它的角动量变大了。但是在旋转参考系中,物体在切向属于平衡状态(在地面参考系中并不是)。那么是什么力来平衡掉来自辐条的切向推力呢?不能是离心力,因为离心力是径向的,我们称这个力为科里奥利力。如果我们沿切向移动一个物体。转盘的角速度为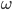 ,物体距圆心的距离为r,地面系上物体的速度为
,物体距圆心的距离为r,地面系上物体的速度为 ,旋转参考系上看物体的速度为
,旋转参考系上看物体的速度为 ,因此有
,因此有 。这个物体受到的向心力为:
。这个物体受到的向心力为: 。上式中的第一项为物体在转动参考系中感受到的向心力,即使参考系不旋转,观察者也会知道这个力,第三项是由于参考系旋转感受到的向心力,第二项为科里奥利力。径向和切向的两个力满足同样的规律,因此可以统一表示为:
。上式中的第一项为物体在转动参考系中感受到的向心力,即使参考系不旋转,观察者也会知道这个力,第三项是由于参考系旋转感受到的向心力,第二项为科里奥利力。径向和切向的两个力满足同样的规律,因此可以统一表示为: 。
。

JQX|Jin
seminar的一个重要价值在于通过交流和讨论让大家经历一个生成知识的过程。我们深入讨论了非惯性参考系下的三种惯性力:惯性力、离心力和科里奥利力。关于"重力是否有反作用力"这一问题。结合非惯性系中牛顿第三定律不再成立的特点,我们给出了一种较新的解释:重力作为离心力与万有引力的合力,由于离心力是惯性力而非真实的相互作用力,因此重力本身也没有反作用力。
另一个重要收获是对离心势能本质的理解——在特定条件下,它可以视为惯性系与非惯性系中动能的差值。这一认识在解决实际问题时非常有用。例如,在前面的细杆例题中,如果要求小环落到杆的中点时在惯性系下的速度,通过"离心势能是动能差值"这一理解,可以给出很好的计算方法。
但需要指出的是,这一理论在物体有切向速度时不再严格成立,因为会出现额外的交叉项 。这引出了一个有趣的问题:是否可以定义一个"科里奥利势能"来描述这个交叉项?对于本次讨论的细杆问题,小环相对细杆只有径向速度而无切向速度,所以"动能差值理论"是完全成立的。关于科里奥利势能的物理意义,将在下期seminar中继续进行讨论。
。这引出了一个有趣的问题:是否可以定义一个"科里奥利势能"来描述这个交叉项?对于本次讨论的细杆问题,小环相对细杆只有径向速度而无切向速度,所以"动能差值理论"是完全成立的。关于科里奥利势能的物理意义,将在下期seminar中继续进行讨论。

前一阵子中午跑完步还有时间,就去单杠那找找年少的感觉。偶然发现几位很特别的小朋友,别人在踢足球、打篮球或嬉戏打闹,他们在自行练习和切磋,几日观察下来,除了自律,还有知识储备等···想到最近跑步活动开展的不错,是不是也应该鼓励和赞助几位开展个健身的小社团呢,至于名字想到“逆熵社”之类,鉴于先有了qiutorun[?],那来个qiutofit何尝不可呢。
“生命如伙,强健有我。”我喜欢伙伴的“伙”和康健的“健”,因为都有个“亻”的偏旁。等高考结束,月考也结束,相信能有不错的方案。
先预祝高考成功~~~

《反叛的科学家》(The Scientist as Rebel)一代传奇物理大师Freeman Dyson的科学反思
萧秀珊译
一个知识人的诤言
如果把形成共识形容成湖面结冰的话,戴森会不遗余力地在冰面上凿洞。
时间很晚了,然而善恶的选择却在敲着我们的门。
理性的反叛者
二十世纪物理学三大人物,爱因斯坦、霍金和费曼。
狐狸伎俩多,刺猬只懂一种。
科学是人类理性与想象特质的自由发挥。(科学是人类对事物的逐步征服,先是时间与空间,再来是物质那类,然后是自己的身体与其他生物体,最后征服的是自身灵魂中的黑暗与邪恶。)
前言
富兰克林没有受过正规教育,也没有继承大笔财产,但在与欧洲贵族的科学竞赛中,击败了这群博学多闻的贵族们。
富兰克林所展现的反叛是经过深思熟虑的反叛,是由理性与仔细考量所驱动,并非由激情与仇恨所驱使。
(以反叛者的身份去的了伟大的成就,因为他们旨在建立新社会,而不是摧毁旧社会。他也了解传统的价值,他伟大到足以看到事情的两面。)
让胜利者来吧,
当愚昧的堡垒倾倒时,
他们会在墙边找到你的身体!
Mathew Arnold
一、当代科学议题
1、反叛的科学家
他们叫那个倒扣的碗为天空
在那之下被禁锢的我们蠕动着活着与死去
不要举手向它求助
因为它
跟你我一样只会无力打滚
Continue reading »
JQX/进取芯 席明纳第8期(2025.5.14)

在力学问题中,速度关联现象较为常见,而加速度是否也存在类似的关联规律呢?

JQX|Jin
一、绳 / 杆模型
一)例题
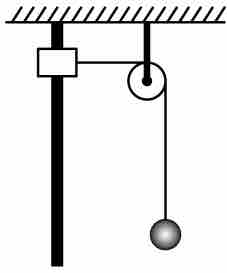
如图所示,物块套在固定竖直杆上,通过轻绳跨过定滑轮与小球相连,初始时刻物块与定滑轮等高。已知物块质量
 ,小球质量
,小球质量  ,杆与滑轮间的水平距离
,杆与滑轮间的水平距离  ,重力加速度
,重力加速度  ,且轻绳和杆长度足够,忽略一切摩擦与空气阻力。现将物块由静止释放,在其下落过程中,求解以下问题:
,且轻绳和杆长度足够,忽略一切摩擦与空气阻力。现将物块由静止释放,在其下落过程中,求解以下问题:1. 物块下降的最大距离
设物块下落的最大高度为
 ,此时小球上升的最大距离为
,此时小球上升的最大距离为  。根据几何关系可知:
。根据几何关系可知:
机械能守恒定律可得:

解得:

2. 系统动能最大时物块的动能
这里有两种方法:
1)写出动能与角度的表达式,进行数学方法求极值。
2)从物理意义上考虑,当系统的重力功率之和为
 时,系统动能达到最大值。
时,系统动能达到最大值。设物块速度为
 ,小球速度为
,小球速度为  ,根据速度关联关系可知:
,根据速度关联关系可知:
由重力功率关系可得:

对物块和小球组成的系统,运用机械能守恒定律求解动能最大值,可得动能最大值为:

3. 物块运动的最大速度
1)原答案解析
答案寻找了一个特殊位置:当物块的速度最大时,加速度为
 ,由于物块和小球被绳牵连,沿绳方向的加速度大小相等,小球的加速度也为
,由于物块和小球被绳牵连,沿绳方向的加速度大小相等,小球的加速度也为  ,所以物块和小球同时达到最大速度,分别为
,所以物块和小球同时达到最大速度,分别为  和
和  。分别对物块和小球列平衡方程得:
。分别对物块和小球列平衡方程得:

由(1)式可求得:
 则:
则:
如图3所示,由物块和小球沿绳方向的速度大小相等得:

由系统的机械能守恒:

联立(2)(3)(4)式解得:


2)对原答案的质疑
原答案认为,既然沿绳方向的速度大小时刻相等,沿绳方向的加速度大小一定会相等,并且找到了一个特殊位置,满足两个物体加速度同时为  。但是,这个理论靠得住脚吗?
。但是,这个理论靠得住脚吗?
设物块的速度为  ,小球的速度为
,小球的速度为  ,二者速度关系为:
,二者速度关系为:
对该速度关系两边求导,可得:
我们发现,不存在两个物体加速度同时等于0的情况。原答案解析是有错误的。
当物块的速度最大时  ,则有
,则有 
对物块有 
对小球有 
对物块与小球组成的机械能守恒,可得  其中
其中  ,
,
联立解得 
二)讨论:加速度关联(沿绳方向加速度相等)满足的条件
1. 速度为零
2. 角速度为零
3.  趋近于
趋近于 
我们也可以进一步推导公式,发现多出一项即为绳的向心加速度。所以,如果出现旋转,在加速度关联时,就要加上向心加速度这一分量。
三)速度关联的三种推导方法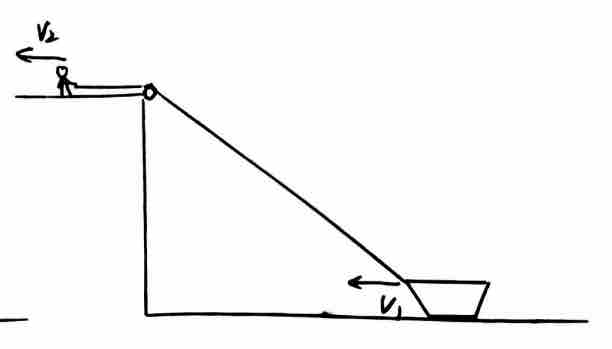
在绳连接船的系统中,根据沿绳方向加速度相等,可得: 其中
其中  为绳与水平方向的夹角。
为绳与水平方向的夹角。
1. 求导法
设船与岸边距离为  ,绳长为
,绳长为  ,定滑轮高度为
,定滑轮高度为  ,根据勾股定理可得:
,根据勾股定理可得:
对时间  求导,得到:
求导,得到:
其中  表示船的速度
表示船的速度  ,
, 表示人收绳的速度
表示人收绳的速度  。可得到:
。可得到:
结合几何关系可推导出:
2. 微元法
取极短时间  ,此时绳转过角度
,此时绳转过角度  。过船所在位置
。过船所在位置  作绳初始位置
作绳初始位置  的垂线
的垂线  ,由于
,由于  ,可近似认为
,可近似认为  。
。
人收绳长度:
船运动距离:
根据  ,有:
,有:

又因为  ,将上述关系代入可得:
,将上述关系代入可得:
约去  ,得到:
,得到:
3. 功率法
考虑到绳为轻质绳,不储存能量,这意味着人拉绳的瞬时功率时刻等于绳对船的作用力的瞬时功率。根据功率公式  ,可列出等式:
,可列出等式:
等式两边拉力  相同,化简后得到:
相同,化简后得到:
拓展例题:虚功原理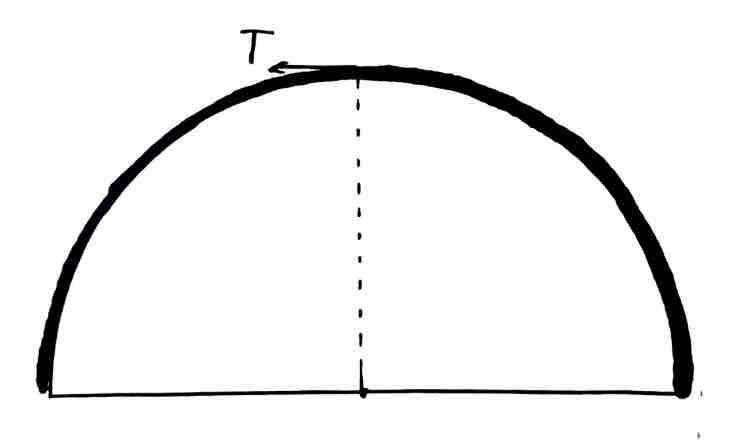
如图所示,一条线密度为  的均匀铁链,静止放置于半径为
的均匀铁链,静止放置于半径为  的光滑半圆形台上。铁链两侧对称下垂且恰好落在半圆末端。试求解铁链在最高点处的拉力
的光滑半圆形台上。铁链两侧对称下垂且恰好落在半圆末端。试求解铁链在最高点处的拉力  。
。
提示:可以认为铁链向左移动很小一段,相当于拉力做功将末端的一小段质量搬运到了最高点。

二、接触模型
1.在接触模型中,两物体接触处的速度关联通常将接触点处的速度沿接触面切线方向和垂直于接触面方向分解,由于两物体始终保持接触,垂直于接触面方向的分速度大小相等。
而在加速度关联方面,垂直于接触面方向的加速度存在关联关系,具体推导过程与绳杆模型相同。


其中:
 为相对速度,
为相对速度, 为曲率半径。
为曲率半径。
若接触面是平面,则垂直于接触面方向的加速度相同。若接触面是曲面,还需考虑向心加速度对加速度关联的影响。这个加速度计算时,速度应为接触点相对于接触面的加速度,半径应为曲率半径。
2. 相对向心加速度的使用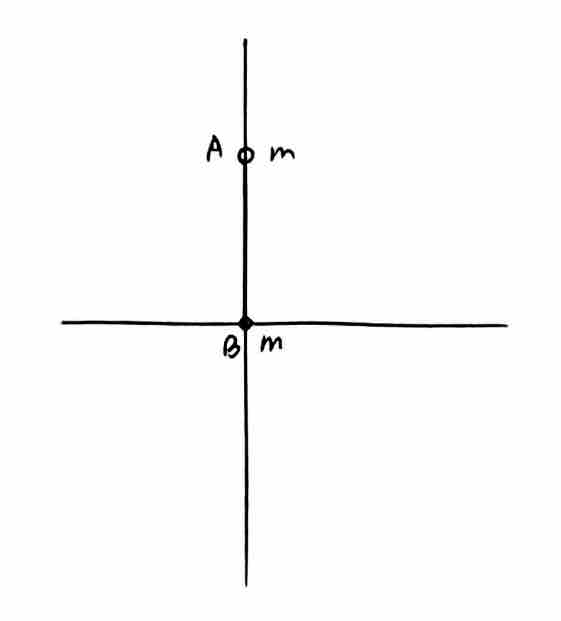
在高中物理中,我们利用向心加速度计算时,带入的速度均为相对于圆心的速度(因为不相对于圆心,也不是圆周运动了)。
例题:两个固定的光滑杆十字放置但不接触,两个质量为  的
的  、
、 两球套在杆上并用铰链通过另一长为
两球套在杆上并用铰链通过另一长为  的直杆相连。初始位置如图所示,轻微扰动
的直杆相连。初始位置如图所示,轻微扰动  球后,求
球后,求  球的最大速度。
球的最大速度。
方法一:
速度关系:
机械能守恒:
联立解得:
通过求导求极值,可得当  时,
时, 取得最大值。
取得最大值。
方法二:相对向心加速度(帅)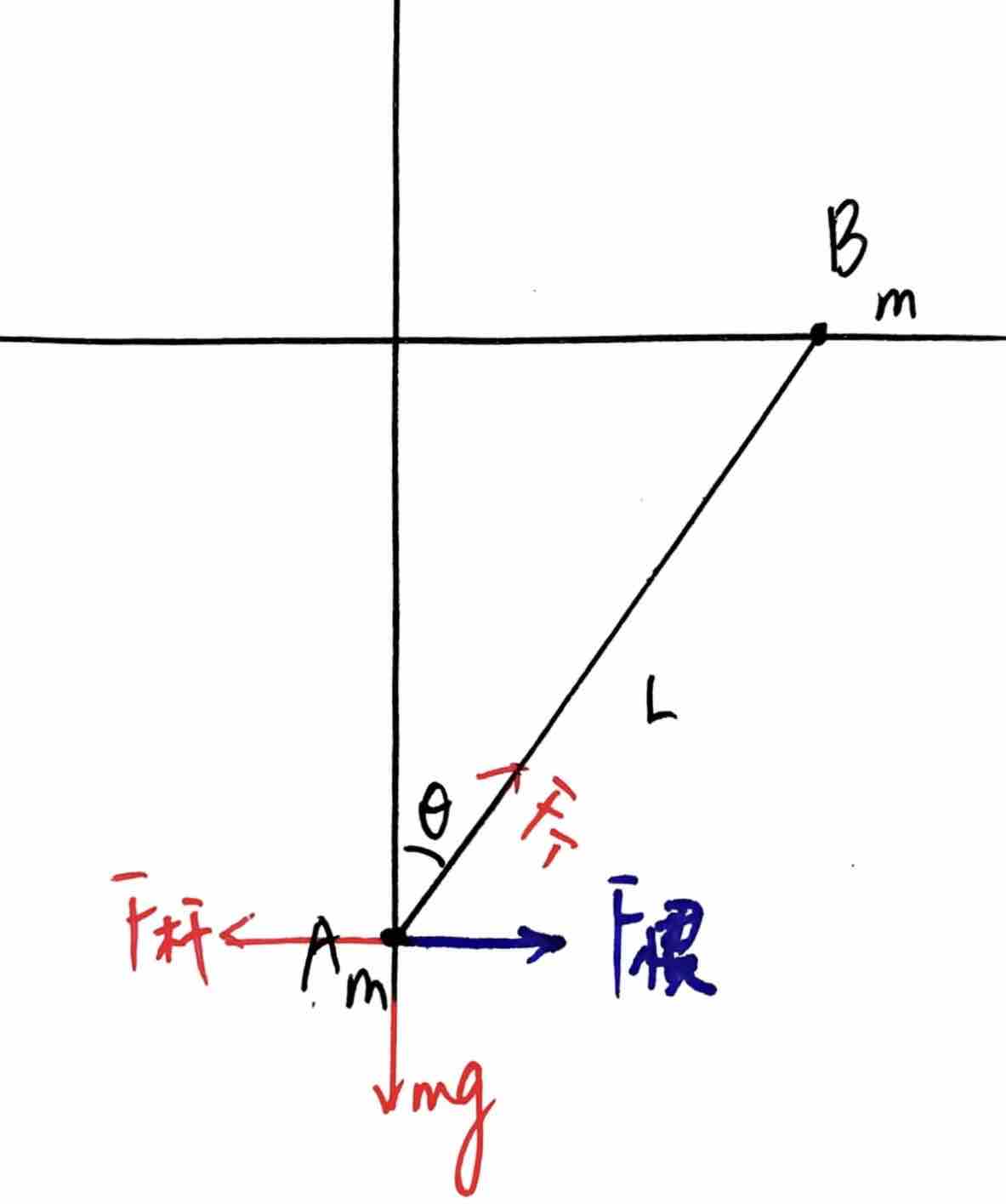
在实际教学中,计算杆上力的时候,经常使用相对运动的方法列圆周运动。本题可以以B球为参考系,则A球相对B球做圆周运动。
那么在A球受力分析时,要引入惯性力(B球的ma),这个力恰好与A球所受杆的力大小相等方向相反(惯性参考系使用质点系牛二分析水平方向),这两个力合力为零。
所以沿杆方向的力只有杆力和重力分力:
速度最大时,A球竖直方向加速度为0,有
再结合机械能守恒和速度关系:  、
、 
解得  ,结果与方法一相同。
,结果与方法一相同。
三、动滑轮模型
一)例题分析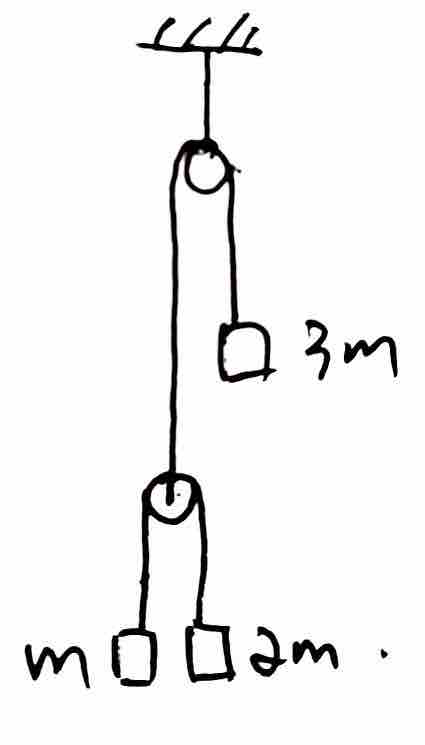
如图,三个已知质量的物块通过轻绳、轻滑轮连接,不计一切阻力,由静止释放,已知重力加速度  ,求三者加速度大小各是多少。
,求三者加速度大小各是多少。
设三个物块质量分别为  、
、 、
、 ,加速度分别为
,加速度分别为  、
、 、
、 ,绳子拉力分别为
,绳子拉力分别为  、
、 。
。
根据牛顿第二定律对三个物块分别列式:
对于质量为  的物块:
的物块:
对于质量为  的物块:
的物块:
对于质量为  的物块:
的物块:
同时,根据滑轮的力学关系有:
根据物块间加速度关联,有:![a_1 - (-a_3) = -[a_2 - (-a_3)]](http://www.qiusir.com/wp-content/plugins/latex/cache/tex_852f0140fc2db328aa97dafea841ee87.gif)
联立求解后,可得:
易错点:
1. 左侧滑轮的加速度关联(换参考系)问题。
2. 滑轮的力学关系。
二)绳拉船问题加滑轮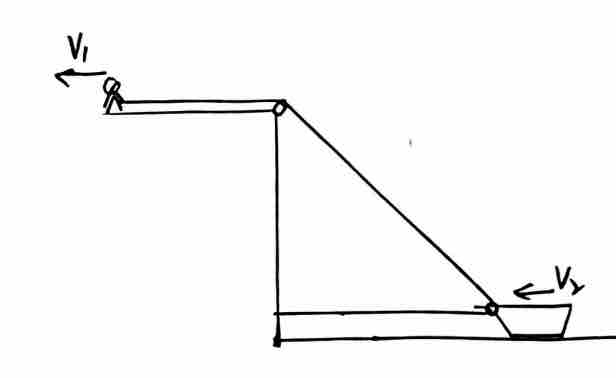
如果将绳拉船问题的船加上一个滑轮,另一端水平连接到岸边,如黑板左中图所示。那么,这个情况下的速度关联如何?
方法一:求导法



对时间求导,
方法二:功率法

方法三:微元法

从物理意义上来看,滑轮的引入在原有速度关联的基础上,增加了水平绳子缩短的速度。
【下期预告】邀请高一六班刘而行同学交流“非惯性参考系与惯性力”···