因为$$a^2+b^2=c^2$$,所以3±4=5
1、重力 基本相互作用
重力和万有引力的关系
2、弹力
自然界的四种基本作用力是不需要接触就能起作用的。
弹簧剪短,串联并联,劲度系数.Hooke law
3、摩擦力
$$F_{f,s}\le \mu_sF_N$$
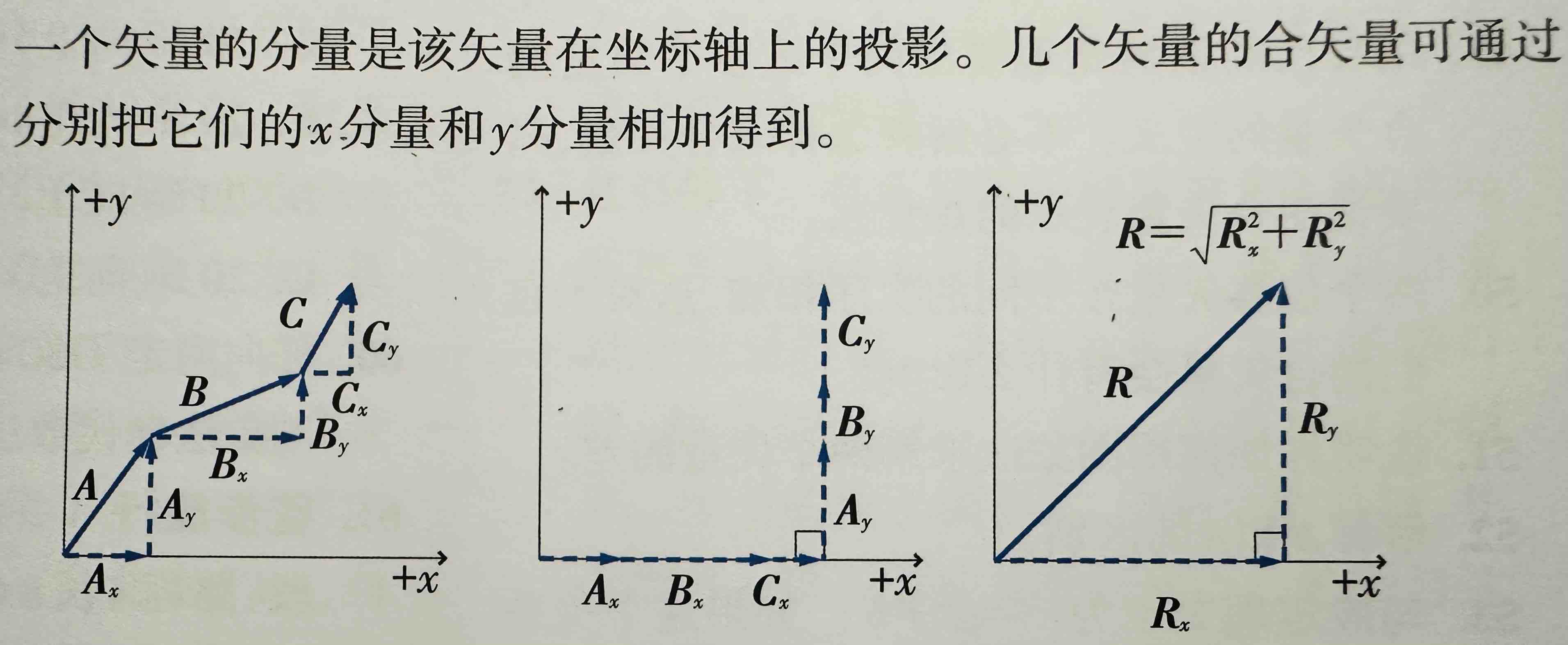
4、力的合成
(F1+F2)^2
三角形法则。
5、力的分解
6、平衡
光滑碗里细线的两个球的受力,战鸽同学的矢量三角形的方法。
日语教材上的分类
▼接触力の例
張力(Tension) T
垂直抗力(Normal Reaction) N
摩擦力(Friction) f
弾性力 kx
▼遠隔力の例
重力 mg
静電気力 qE
磁力
核力
[鉛直方向]Tsin30°=W
Hookeの法則(法则一说来自日语啊?)
Atwoodの器械
$$\frac{1}{2}mv^2$$
滚动摩擦$$F_r=\frac{f}{r}F_N$$滚动摩擦系数f(量纲是长度)表达了支持力$$F_N$$与摩擦力矩M之间的比例关系。$$M=r\cdot F_r=fF_N$$
一道立体模型的摩擦力题
斜面置物

正六边形对矢量合成运算的多种训练方法。
滑动摩擦力压力和弹力成比例,合力的方向不变,可以转化几何表述平衡态下另外外力随角度的大小变化,以及摩擦力和功率的变化情况。
定角$$\theta$$的圆锥上套一质量为m的质地均匀的圆环,求环的张力。
$$T=\frac{mg cot\frac{\theta}{2}}{2\pi}$$
静力学不错的题目,风力垂直接触面,用泰勒斯定理,摩擦系数大于1的出题者意图不错
有时间找一道风筝的问题
B摩擦力变化比较特别
昨天那位前几天哭鼻子的孩子问了一道不错的静力学问题。
水平外力让粗糙斜面上物体静止的力的范围,用水平正交分解、沿斜线和垂直斜线正交分解和摩擦角$$[tan(a-b)g,tan(a+b)g$$
还真是静力学的经典
等效重力
风力方向
最后选项挺特别。