
热
T[K]=273+t[℃]
(通过PV=nRT到三个气体定律)
气体压强微观模型的推导。(这部分和台湾有的教材类似)
定压变化、定积变化、断热变化
$$T(K)=273.15+t(^\circ C)$$
$$F_1 \frac{2L}{v_{1x}}=2mv_{1x}$$,$$F_1=\frac{mv_{1x}^2}{L}$$,$$P=\frac{F}{A}=\frac{Nm\bar{v_{x}^2}}{V}$$,$$P=\frac{1}{3}\rho \bar{v^2}$$(气体压强后我们感受到的风力的关联因素)
$$\bar{E_k}=\frac{3PV}{2N}=\frac{3nRT}{2N}=\frac{3RT}{2N_0}=\frac{3}{2}kT$$(台湾教材翰林版[?])
设边长为L的立方体内,x方向单个气体分子动量变化$$2mv_x$$,时间t内碰撞次数$$\frac{v_xt}{2L}$$,$$2mv_x\times\frac{v_xt}{2L}$$,$$Ft=\frac{m\bar{v_{x}^2} t}{L}\times N$$,$$F=\frac{Nm\bar{v_{x}^2}}{3L}$$,$$P=\frac{F}{L^2}=\frac{Nm\bar{v_{x}^2}}{3V}$$
$$P=nRT=\frac{N}{N_A}RT$$,$$\frac{1}{2}m\bar{v^2}=\frac{3}{2}\frac{R}{N_A}T=\frac{3}{2}kT$$
理想气体内能
$$U=N\times\frac{1}{2}m\bar{v^2}=\frac{3}{2}nRT$$
对于等压变化气体做功,$$W=P\Delta V=nR\Delta T$$
电磁
$$k=\frac{1}{4\pi\varepsilon}$$,$$N=\frac{kQ}{r^2}\times 4\pi r^2=4\pi kQ=\frac{Q}{\varepsilon}$$
法则(定律)$$\varepsilon$$诱電率诱電体的诱電率
$$\frac{1}{2}mv^2+qU$$=一定(类比重力势能的qV)
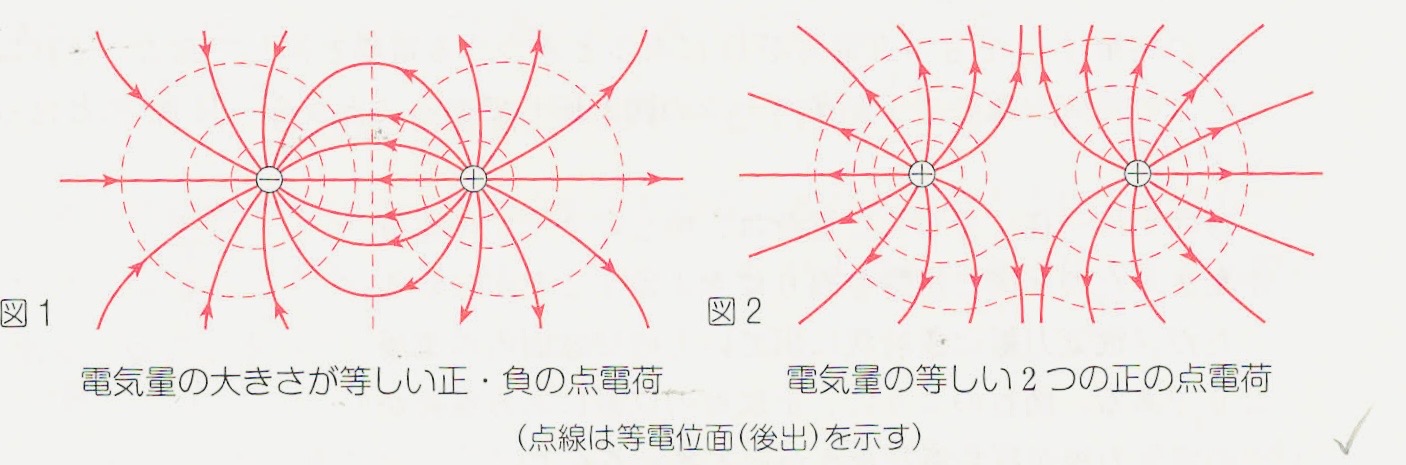
(上图和很多网图相比那是相对精确了)
点电荷的电势类比万有引力,并用高度坡度下滑类比。
等电位面(等势面)
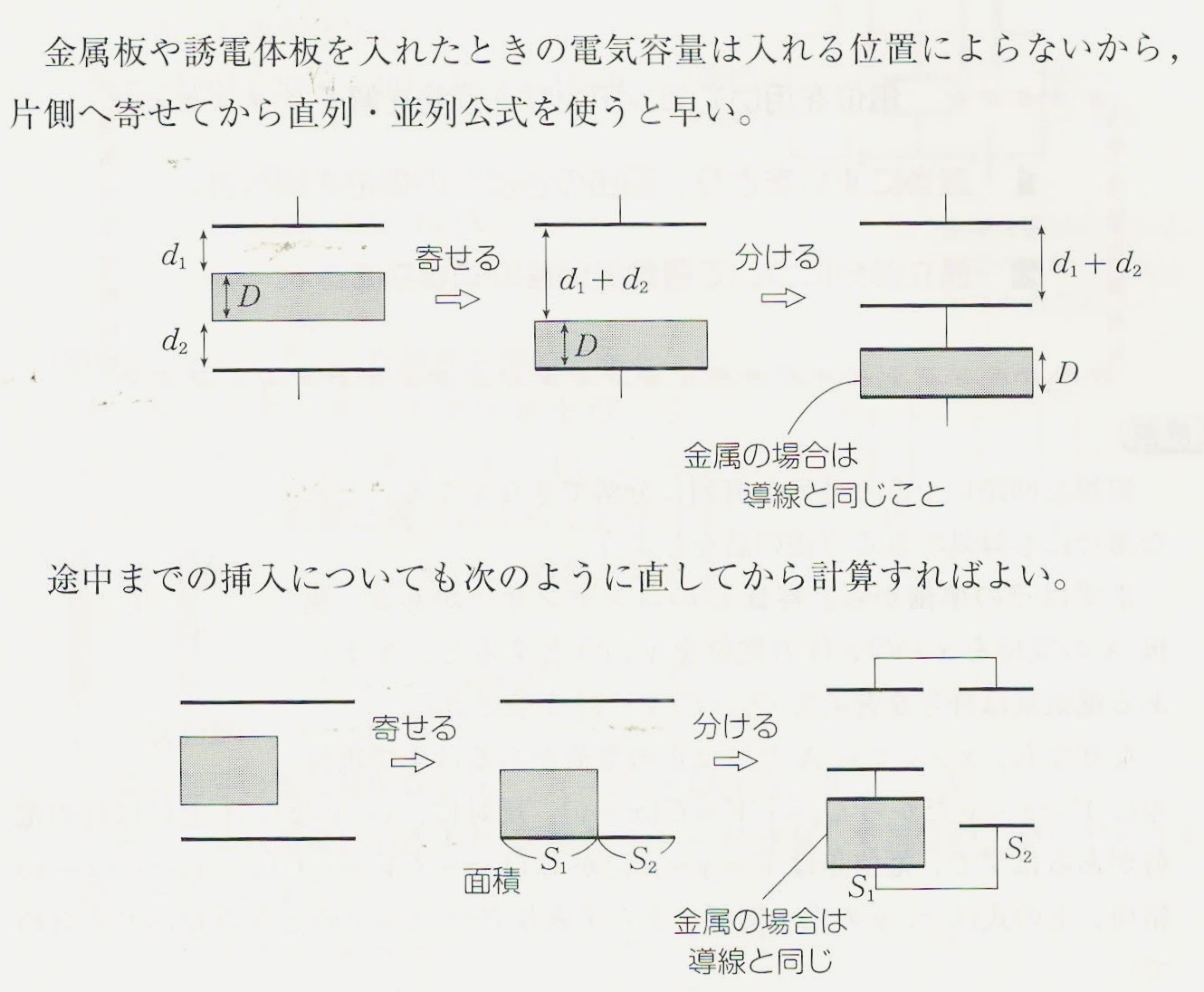
(电容器内部填入导体的等效变形很漂亮的简化)
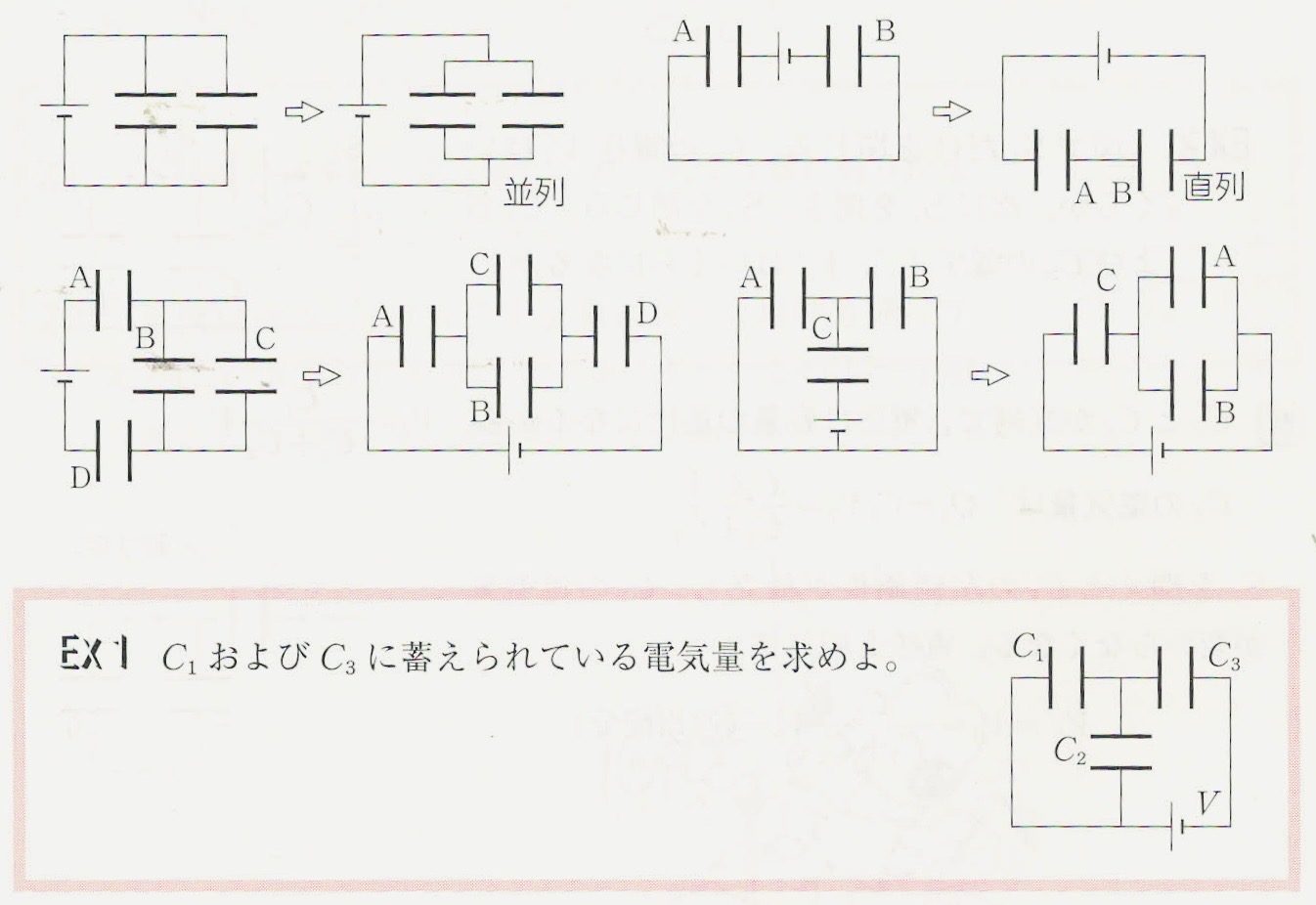
电容的串并联图和电阻的等效变换一样(图很赞)
电容储存能量的公式
平行板电容器板间吸引力
假定上极板向上平移一小段距离,从电容器能量的变化考虑$$F\Delta d=\Delta U$$
$$\Delta U=\frac{Q^2}{2C’}-\frac{Q^2}{2C}=\frac{Q^2\Delta d}{2Cd}$$
综上,$$F=\frac{Q^2}{2Cd}$$
电子在导线中收到抵抗力f=kv,等速运动时,kv=qE,$$v=\frac{qE}{k}=\frac{qU}{kl}$$,又由$$I=vnqS$$,$$I=qnS`$$
透磁率
$$F=k_m\frac{m_1m_2}{r^2}$$(m[Wb])
安培力F=IBl
$$Z=\sqrt{R^2+(\omega L+\frac{1}{\omega C})^2}$$
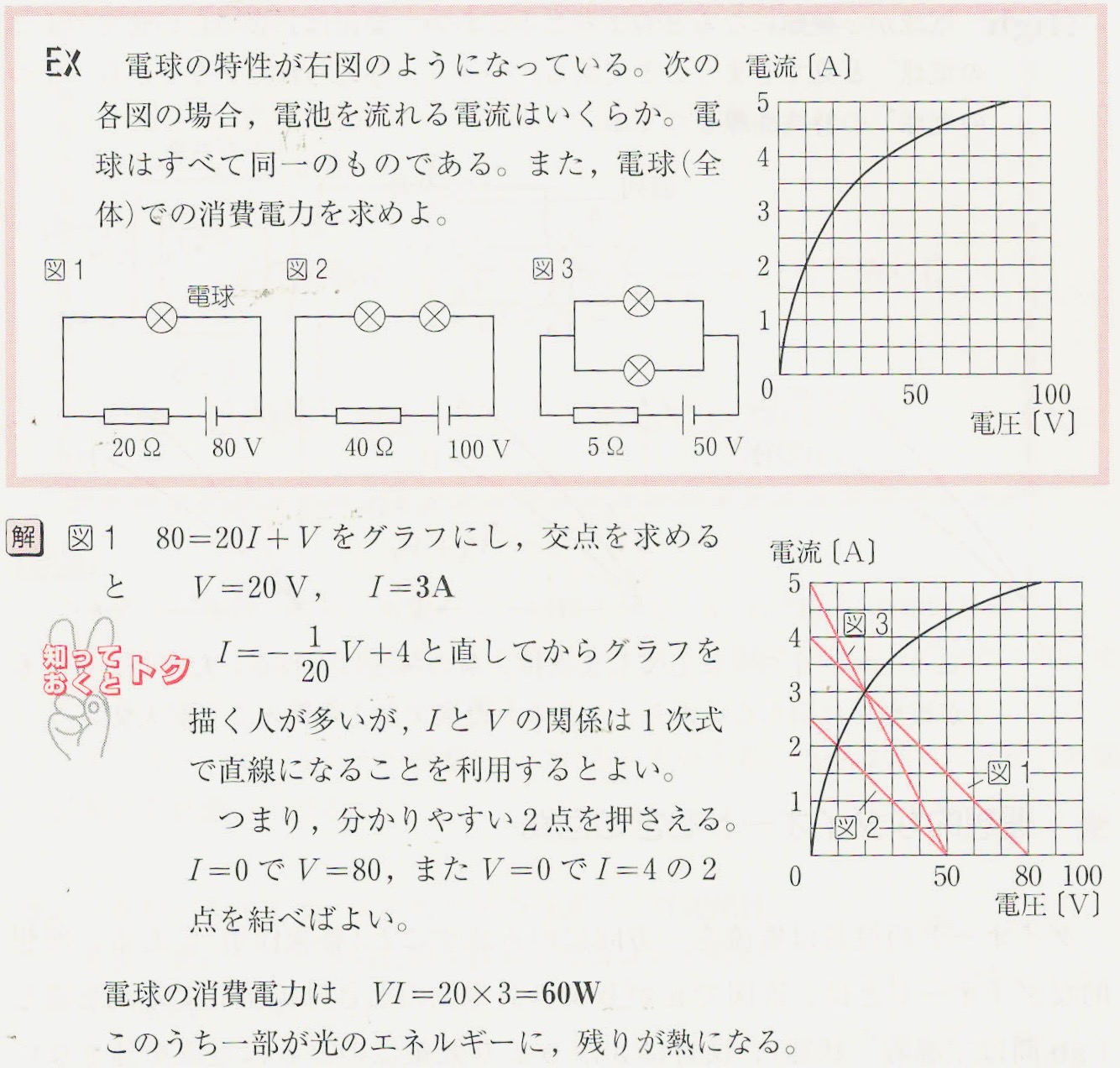
(这里一般习惯用U-I图像,通常用 $$E=U+Ir$$、$$E=U+2Ir$$、$$E=2U+Ir$$)
磁场诱导(电磁感应)
诱导起電力U=vBl $$U=-N\frac{\Delta\Phi}{\Delta t}$$
电波、赤外线、可视光线…
特殊导线的磁场
原子
光电效果、限界振动数(台阶的图示很妙)
$$\frac{1}{2}mv_{max}^2=h\nu-W$$
光强增大,单位时间光子数增多(同一频率)
(光子打电子,平面动量守恒的正交分解,近似求解波长变化量,赞)
光子与电子的碰撞:
$$\frac{h}{\lambda}=\frac{h}{\lambda’}cos\theta+mv cos\phi$$
$$0=\frac{h}{\lambda’}sin\theta-mv sin\phi$$

$$h\frac{c}{\lambda}=h\frac{c}{\lambda’}+\frac{1}{2}mv^2$$
(一系列化简和近似)$$\lambda’-\lambda=\frac{h}{mc}(1-cos\theta)$$
($$2dsin\theta=n\lambda$$干涉条件)
(氢原子波尔模型$$2\pi r=n\frac{h}{mv}$$,然后推导出半径、能量与$$n^2$$反比)(里德常数推导)
$$\frac{mv^2}{r}=\frac{ke^2}{r^2}$$,$$2\pi r=n\frac{h}{mv}$$,$$r_n=\frac{h^2}{4\pi^2kme^2}\cdot n^2$$
$$U=-\frac{ke^2}{r}$$,$$E=-\frac{ke^2}{2r}$$,$$E_n=-\frac{2\pi^2k^2me^4}{h^2}\cdot \frac{1}{n^2}$$
(1u12gC12)$$1u=\frac{12\times10^{-3}}{N_A}\times \frac{1}{12}=\frac{1}{10^3N_A}kg$$
放射性崩壞、原子番号
陽子(质子)、电子、陽电子、中性子(中子)$$E=mc^2$$、$$\Delta E=\Delta mc^2$$
(经常出现保存则)
质量银行,预金+现今=一定

核分裂、核融合、γ崩壊、质量欠损
基底状态、励起状态
(这本书对于α、β和γ在磁场和电场中偏转的图示不够准确。)(β偏转比较大)
合成公式(辅助角)$$asin\theta+bcos\theta=\sqrt{a^2+b^2}sin(\theta+\phi)$$
二次函数的日本化简挺好
$$ax^2+2b’x+c=0$$,解为$$x=\frac{-b’\pm\sqrt{b’^2-ac}}{a}$$
三角函数公式

年终回顾
气体压强的推导过程要更熟练一点,可以转化成风的阻力问题。
$$\frac{1}{2}mv^2+qU$$=一定(类比重力势能的qU)
图示的辅助角公式用的很巧妙,会用就好。
小角度的近似应该加入。
$$sin\theta\approx\theta$$
$$cos\theta\approx 1-\frac{1}{2}\theta^2$$
