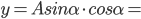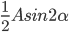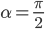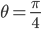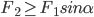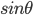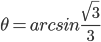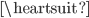本学期高二物理的课程安排是先3-5动量、3-4振动和波,最后再回到3-5。月考前的复习课我采用从简谐振动图像引入,再次采用王聪的方法关联,强调了速度时间图像的视角复习碰撞...
毕业的学生回访时常有“早把当年学的那些还给老师了”的玩笑,而回过头来看,学生毕业并非要从学校和老师那带走什么,反倒是要留下点什么:留下美好的回忆在校园凝固,留下思维的火花在教室相传~2013.1
王聪同学是我以前的物理课代表,最初是他很坚持地分享了从简谐振动的角度分析和解决弹性碰撞的相关问题。前些天已经和1、2等班的学生分享了“王聪方法”,使复杂的结论变得相对形象和简单一些,学生基本被接受。这里整理一下以备他(他时、他人)用...
这里要涉及到的主要物理图景:光滑水平面上,质量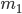 的木块以速度
的木块以速度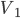 和质量
和质量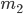 ,速度
,速度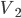 的木块发生弹性碰撞。假定木块间存在理想弹簧,此处用来放大弹性碰撞的过程...
的木块发生弹性碰撞。假定木块间存在理想弹簧,此处用来放大弹性碰撞的过程...
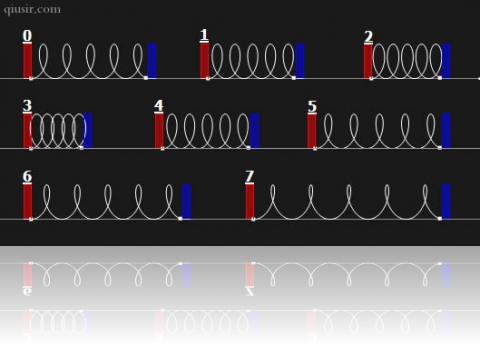
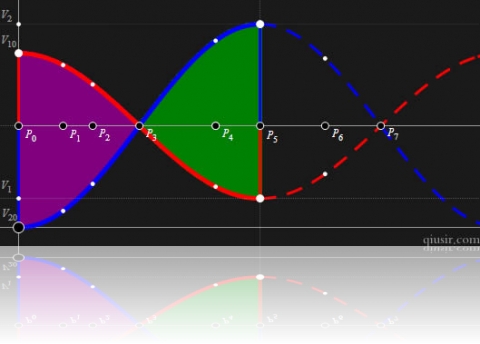
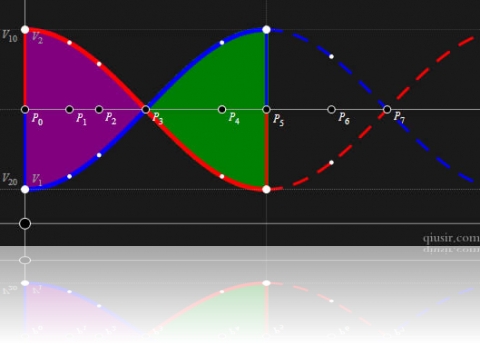
如果两物体和弹簧相连,我们把碰撞的过程分解成上面7个过程,后面需要对应标号理解的地方。
当弹簧形变量最大时两物体共同速度为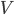 ,假定
,假定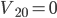 ,
,
由系统动量守恒得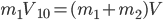 ,所以由
,所以由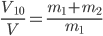 ,此式可以理解为
,此式可以理解为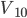 被分为
被分为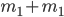 份,V对应为
份,V对应为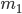 份。(速度比例转化为质量比例)
份。(速度比例转化为质量比例)
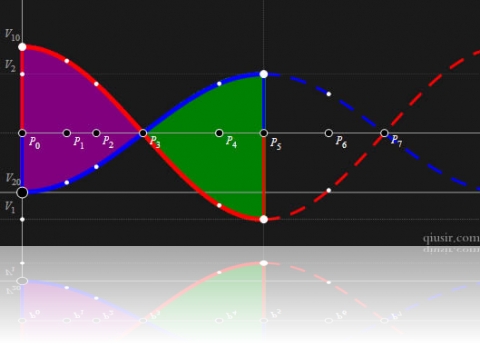
好了,我们把两个光滑水平面上两木块的运动理解为整体(质心)以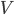 匀速运动,而他们分别又以动的质心为平衡位置的简谐振动的叠加。(弹簧的弹力提供回复力)
匀速运动,而他们分别又以动的质心为平衡位置的简谐振动的叠加。(弹簧的弹力提供回复力)
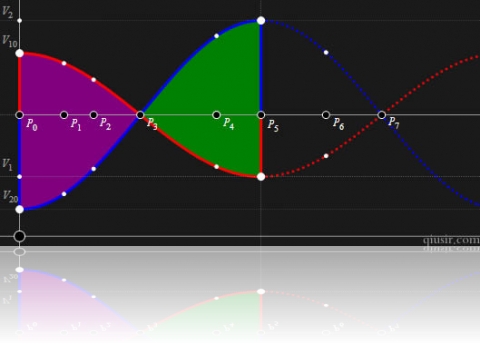
按照上面的比例关系分析上图,利用简谐振动速度时间图像的正弦函数特性,可以看到
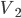
和
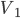
对应的质量比例关系分别为
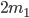
和
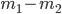
(特别注意上图中竖直线段,红色的
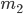
和蓝色的
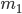
)。这样就很容易得到:
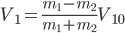
;
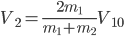
更一般的情况是
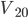
不等于零,利用上图坐标平移的方法,时间轴向上平移
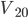
,
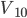
变为
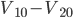
,接下来方法同上,只不过计算结果上需要再加上平移量
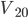
。
得到更一般的弹性碰撞公式:
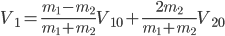
;
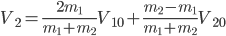
。
通过前面的代数式,
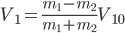
我们很容易知道
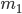
<
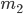
时小球会反弹,当然这个结论也可以通过上图画出。通过上图我们也可以直观明白弹性碰撞和完全非弹性碰撞会使得前面小球获得最大和最小的速度(动能)。(
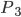
及其以后的位置可以等效为碰撞结束的位置,弹性势能没有完全释放的等效称非弹性碰撞)
不管
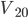
是否为零。如果两物体的质量相等,速度对应的质量比必然是中点,这样我们自然看到的是交换速度的结果了。
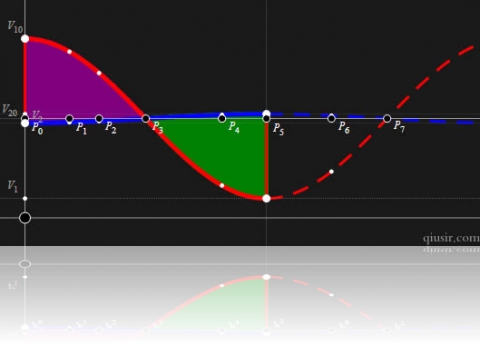
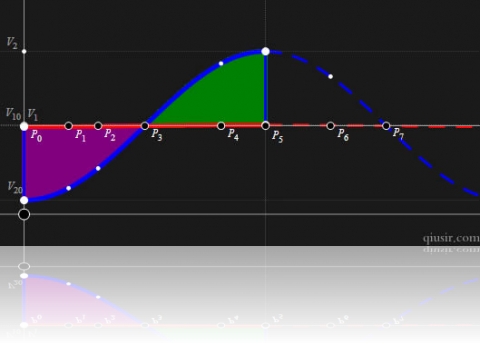
最后的两幅图演示的两物体质量悬殊很大,极限情况是
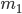
>>
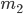
和
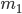
< <
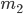
。无穷大物体速度不变,想当于是质心,另一物体相对它简谐振动。
对于此处所有的图示中,
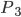
对应的是完全非弹性碰撞,
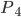
对应的是非弹性碰撞,而
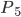
则是上面公式结论中的弹性碰撞。如果弹簧是被连接到两物体上的,那共速度点
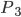
对应弹簧压缩最短位置,而
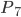
则对应的是弹簧拉伸最长的位置。
尽管此处涉及到竞赛中提到的质心匀速与简谐叠加的超纲内容,但仅仅从速度时间图像斜率是加速度的知识点,外加一点对称的猜想就可以独自解决。而这里解释的目的仅仅是倡导学生用自己的方法去真正的研究一个物理的模型,相信自己的探索会对其他人,同学甚至老师有作用。当然作为老师也期待更多的学生方法被老师习得。
PS.说到简谐振动,我也联想到时下和谐社会的提法:
真正的和谐社会该是物质和精神极大丰富的共产主义,而原始社会物质和精神的简单构成,从物理角度看应该叫做简谐社会:)那眼下社会主义初级阶段的和谐提法,唯一的可能就是分隔...哈哈,不多说了。
PS.高三10班的姚贯匀同学结合课上的讲解,从代数的方法把结论做了另外的等效:

,

。结合图像关于共速的对称性,或弹簧伸长量和压缩量相等,用平均速度的角度可能更容易理解,

,

~2021.10
GSP5文件下载:GSP-王聪方法 (6378)
2021
姚贯匀同学把这种对称的想法转化为
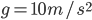 ,根据给定条件求各点的瞬时速度。
,根据给定条件求各点的瞬时速度。
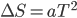 ,
,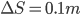 ,水平方向
,水平方向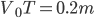 ,求得
,求得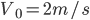 ...找到了乱绳子的头就好办了。
...找到了乱绳子的头就好办了。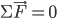
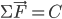
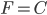
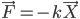
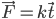
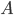
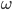
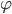
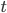
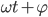
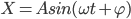
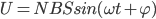

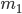
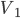
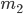
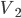
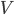
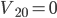
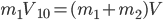
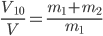
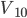
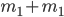
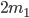
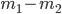
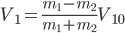
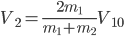
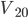
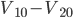
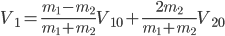
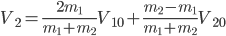
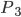





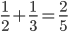
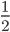
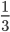
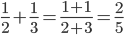
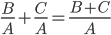
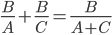
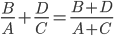
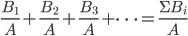
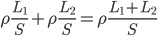
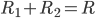
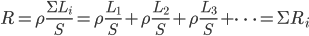
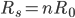
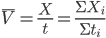
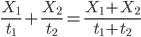
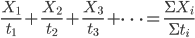
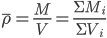
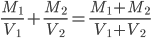
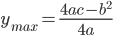
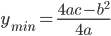
![A+B+C\geq3\sqrt[3]{ABC}](http://www.qiusir.com/wp-content/plugins/latex/cache/tex_571f356391246c2adb723fe4687d811b.gif)