



·[?]无穷递缩等比数列的物理题
JQX/进取芯 席明纳第7期(2025.5.8)

无限常摆长单摆周期问题
零、关于
这个公式是Qiusir在JQX第四期与新疆部学生进行头脑风暴时用到的公式。
根据天体运动中万有引力充当向心力,可以推导近地卫星(贴地卫星)的周期公式,为 ,这个公式很容易让人想到摆长为R单摆的周期,可事实上是这样吗?
,这个公式很容易让人想到摆长为R单摆的周期,可事实上是这样吗?
一、关于
后来讨论的过程中,学生提到他想表达的公式是这个。这个公式可以看做一个小球在圆轨道做小振幅往复运动的周期(等效单摆)。
二、从能量角度推导简谐振动的动力学方程和单摆周期公式
1. 简谐运动
简谐运动满足能量守恒方程: ,
,
简化这个方程,即当动力学方程满足 (
( 为常数)时,可判定为简谐运动。其中,
为常数)时,可判定为简谐运动。其中, 定义为角频率
定义为角频率 的平方。
的平方。
2. 单摆
选取单摆摆动的最低点作为重力势能零点。对于摆角为 的任意位置,根据机械能守恒定律,单摆系统的总能量
的任意位置,根据机械能守恒定律,单摆系统的总能量 满足方程
满足方程 ,其中
,其中 为摆球质量,
为摆球质量, 为摆球线速度,
为摆球线速度, 为摆长,
为摆长, 为重力加速度。
为重力加速度。
根据圆周运动线速度与角速度关系 ,且角速度
,且角速度 可表示为摆角
可表示为摆角 对时间的一阶导数
对时间的一阶导数 ,同时,利用小角度近似条件(当
,同时,利用小角度近似条件(当 时),
时), 可展开为
可展开为 。
。
将上述关系代入能量方程,可得:
由于在小角度下 (
( 为摆球偏离平衡位置的水平位移),将其代入上式,整理后得到:
为摆球偏离平衡位置的水平位移),将其代入上式,整理后得到: 。对比简谐运动的动力学方程,可得出单摆运动的角频率
。对比简谐运动的动力学方程,可得出单摆运动的角频率 。
。
可得到单摆的周期公式:
三、无限摆长问题的提出
我们知道单摆的周期公式是 ,现在我们来思考一下,当摆长
,现在我们来思考一下,当摆长 趋于无穷大,还有当摆长
趋于无穷大,还有当摆长 等于地球半径的时候,这个周期会是多少呢?
等于地球半径的时候,这个周期会是多少呢?
我们先来推导一下单摆周期公式。
当单摆的摆角 极小时,重力沿圆弧切线方向的分力
极小时,重力沿圆弧切线方向的分力 作为回复力。
作为回复力。
由于摆角 极小,此时
极小,此时 ,且
,且 ,有回复力
,有回复力 。设
。设 ,则回复力
,则回复力 ,这意味着单摆在摆角很小时做简谐运动。把
,这意味着单摆在摆角很小时做简谐运动。把 代入简谐运动周期公式
代入简谐运动周期公式 ,便能推导得出相应结果。
,便能推导得出相应结果。
那么,当摆长无限大时,周期应该为多少呢?是无穷大吗?我们慢慢道来,先来看一下这个情况:
四、近地卫星周期
万有引力充当向心力,可以推得 ,另外,如果使用近地卫星周期可以求密度的结论:
,另外,如果使用近地卫星周期可以求密度的结论: ,将密度反向带回,也可以推导周期。
,将密度反向带回,也可以推导周期。
五、"地下铁"周期
我们假设在地球赤道对称两级挖通一个隧道,设地球半径为 ,质量为
,质量为 。在隧道一端由静止释放一个物体,质量为
。在隧道一端由静止释放一个物体,质量为 ,与地心的距离记为
,与地心的距离记为 。我们来分析一下这个物体的运动。
。我们来分析一下这个物体的运动。
我们知道理想球壳对内部物体的引力合力为零,在这个物体在隧道里面运动中距离地心 处时,所受引力等效于半径为
处时,所受引力等效于半径为 的部分地球对其施加的引力。
的部分地球对其施加的引力。
球体质量公式 (
( 为地球平均密度),可推导出半径为
为地球平均密度),可推导出半径为 的球体质量
的球体质量 。结合
。结合 、
、 、
、 ,可得到
,可得到 ,图像请见黑板。带入简谐周期公式,容易算得
,图像请见黑板。带入简谐周期公式,容易算得 。
。
可以发现,"地下铁"周期的计算结果,与近地卫星的周期数值是相等的,如果在地下铁释放物体的同时,在地面同时发射一颗近地卫星,会发现二者在各自轨道上的运动具有同步性(投影共线),这一现象背后其实蕴含着简谐运动是匀速圆周运动分运动的物理规律。
如果我们将地下铁的轨道换到更高纬度,经过计算(涉及到受力分解等,过程请尝试自行推导)依然可以算得 ,如果我们进一步提高纬度,将纬度极限到北极附近非常小的一部分,那么这个往复运动,应该可以视为无限摆长的单摆运动(摆长无限,近似于直线运动),那么,这个无限摆长的单摆周期,竟然不是无穷大,而是
,如果我们进一步提高纬度,将纬度极限到北极附近非常小的一部分,那么这个往复运动,应该可以视为无限摆长的单摆运动(摆长无限,近似于直线运动),那么,这个无限摆长的单摆周期,竟然不是无穷大,而是 。
。
六、单摆周期公式的修正
通过前面的讨论我们发现,传统单摆周期公式在特殊情况下需要修正。在推导单摆公式时,我们默认重力场类似匀强电场一样方向不变,但实际将视角扩大到地球半径尺度下,我们可以发现其实重力方向是指向地心(忽略自转),那么修正后的单摆周期公式是什么呢?
如黑板七图所示,设摆长为 ,地球半径为
,地球半径为 。万有引力即为重力,
。万有引力即为重力,
回复力
基于小角度近似关系 ,有
,有
再根据小角度几何关系,有
考虑到回复力方向与位移方向的反向关系,进而得到:
回复力系数为 ,代入简谐振动周期公式
,代入简谐振动周期公式  ,
,
综上,单摆周期的最终表达式为:
这个公式中的摆长,可以等效为两个摆长并联的结果,我们前几期探讨了约化质量也是这个模式,这个难道是"约化长度"?
七、单摆公式修正后的结论
根据修正公式,我们可以发现以下结论:
当l相对R足够小时,该公式就近似于传统单摆周期公式,这也解释了为什么在日常使用传统公式计算普通单摆周期时能得到较为准确的结果。
而当l与R处于相近数量级时,二者差异显著,必须使用修正公式进行计算,
当 时,
时, 。
。
当  无限大时,单摆的周期
无限大时,单摆的周期  。该结果与此前推导的近地卫星周期、"地下铁" 周期数值吻合。
。该结果与此前推导的近地卫星周期、"地下铁" 周期数值吻合。
八、静电场中的简谐运动
我们再来说说关于电场的问题。如黑板8图,假设有一个正电荷 和一个负电荷
和一个负电荷 ,固定在距离为
,固定在距离为 的位置上,延长线有点
的位置上,延长线有点 ,与负电荷q 的距离也是
,与负电荷q 的距离也是 。
。
我们来分析一下在 点两侧极短的距离内,有一个正电荷
点两侧极短的距离内,有一个正电荷 释放之后的运动情况:
释放之后的运动情况:
根据库仑定律可得电荷所受合力 (其中
(其中 是释放的电荷)
是释放的电荷)
我们使用AI软件帮我们进行一些体力操作,把这个力 泰勒展开展开一下,
泰勒展开展开一下,
因为 远远小于
远远小于 ,所以我们可以把一些高阶无穷小项忽略掉,有
,所以我们可以把一些高阶无穷小项忽略掉,有 ,满足简谐运动回复力关系。
,满足简谐运动回复力关系。
从势能的角度来看,我们知道势能和功的关系是 ,我们对势能求导就可以得到力。同样的,我们如果写出势能与位移的表达式,进行求导,同样也可以得到力的表达式。
,我们对势能求导就可以得到力。同样的,我们如果写出势能与位移的表达式,进行求导,同样也可以得到力的表达式。
九、势能的极值附近,物理做简谐运动
肖老师补充:其实对于势能极值的位置,在附近做往复运动大多(并不是所有)可以认为是一种简谐运动。
如果将势能的表达式进行求导,泰勒展开后忽略高阶小量,可以得到力与位移的关系(满足回复力形式),再将力进行求导,得到的数值即为回复力常量k,进而可以求解周期等。
其实,我们在第二部分用能量进行求解单摆周期的过程,完全可以只分析势能,推导过程可以非常简化如下:
单摆的重力势能表达式为:
当摆角 很小时(满足
很小时(满足 ),重力势能可近似为:
),重力势能可近似为:
结合单摆小角度摆动时,摆球位移 与摆长
与摆长 、摆角
、摆角 的关系
的关系 ,进一步推导可得:
,进一步推导可得:
求二阶导数,得到 ,即为k值。
,即为k值。
十、利用泰勒展开进一步分析
势能的一阶导为该势能所对应的保守力: ,在平衡位置附近,力关于位置近似呈线性关系:
,在平衡位置附近,力关于位置近似呈线性关系: ,这与简谐振动的回复力形式相同。因此物体近似做简谐振动。其中
,这与简谐振动的回复力形式相同。因此物体近似做简谐振动。其中 ,是等效劲度系数。
,是等效劲度系数。
泰勒展开的一般形式为:
我们把势能U(x)在平衡位置附近展开得到: ,由于势能在平衡位置的一阶导数为零,对于足够小的位移,略去三阶以后的项,可近似得到:
,由于势能在平衡位置的一阶导数为零,对于足够小的位移,略去三阶以后的项,可近似得到: 。
。
简谐振子势能的标准形式为: ,因此我们可以看出等效劲度系数k为:
,因此我们可以看出等效劲度系数k为: 。
。

【下期预告】加速度的关联···
速度关联问题是高中物理运动合成中的难点之一。速度可以关联,加速度也可以关联吗?
下次席明纳,金老师将从一道经典习题入手,探寻三种常见模型的速度、加速度关联的本质,敬请期待。
JQX/进取芯 席明纳第6期(2025.4.29)


一、水平弹簧双球系统的简谐振动分析
水平面上有两个质量分别为 和
和 的两个小球,中间由一个劲度系数为k的弹簧连接。我们分析该系统做简谐振动的性质。
的两个小球,中间由一个劲度系数为k的弹簧连接。我们分析该系统做简谐振动的性质。
1.求周期:由牛顿第二定律,两个小球的运动方程是: ,
,
 ,将两个方程联立可得:
,将两个方程联立可得: ,化简为:
,化简为: 。引入约化质量:
。引入约化质量: ,可以看到振动方程有简谐振动的形式,振动的频率为:
,可以看到振动方程有简谐振动的形式,振动的频率为: ,根据周期公式:
,根据周期公式: 。该系统可等效为质量为
。该系统可等效为质量为 的单质点在弹簧力作用下的简谐运动。
的单质点在弹簧力作用下的简谐运动。
2.两个小球的振幅:根据能量守恒定律: ,可得:
,可得: ,两个小球的振幅按照质量分配,
,两个小球的振幅按照质量分配, 。
。
求任意时刻两个小球的位置坐标:以质心为参考系:两个小球分别做简谐振动,根据动量守衡定律,速度和相对质心位移按照质量的反比分配,坐标分别为 。
。
3.两个小球的位置坐标:回到地面系,质心速度为 ,为简化运算,以初始时刻质心坐标为坐标原点,质心位移为
,为简化运算,以初始时刻质心坐标为坐标原点,质心位移为 。两个小球在地面参考系下的位置坐标为:
。两个小球在地面参考系下的位置坐标为: ,
,
 。附:若两个小球质量相等,会出现很有趣的结果,在地面参考系下,两个小球相差
。附:若两个小球质量相等,会出现很有趣的结果,在地面参考系下,两个小球相差 个相位,平均而言,两个小球在推和拉的过程整体向右运动,但是它们将交替达到静止,一个速度最大时,另一个速度为零。
个相位,平均而言,两个小球在推和拉的过程整体向右运动,但是它们将交替达到静止,一个速度最大时,另一个速度为零。
二、竖直弹簧双球系统的简谐振动分析
将两个小球与弹簧组成的系统用细线竖直悬挂,并处于静止状态。现将细线烧断,试分析两个小球的运动?同水平方向,两个小球的牛二定律同样满足简谐振动的质点运动方程,因此在质心系两个小球将同样做简谐振动,其振幅和周期的分析方法与水平方向的情形相同,结论一致。但是在地面参考系中,质心在做自由落体运动,运动方程会稍有不同,这里不做详细推导。
三、双星问题
两个质量分别为 的两个天体,距离为r,引力大小为
的两个天体,距离为r,引力大小为 ,根据牛顿第二定律,对两个物体分别有
,根据牛顿第二定律,对两个物体分别有 。两个星体的相对加速度为
。两个星体的相对加速度为 ,引入约化质量
,引入约化质量 ,根据向心力公式和牛顿第二定律:
,根据向心力公式和牛顿第二定律: ,解得周期T为:
,解得周期T为: 。与我们常规推导方法相同。
。与我们常规推导方法相同。
上述三个问题虽然不同,但是核心都是利用约化质量和相对加速度来把二体问题简化为单质点问题,双星问题的周期是开普勒第三定律的推广形式,这里用到了高考模式下的星体在引力作用下做圆周运动的简单解,更普遍的形式应该为椭圆。值得一提的是我们利用约化质量处理了二体问题,自然就会想到有没有类似的方法来处理三体甚至其他的多体问题。看过小说或电视剧“三体”的同学们应该都知道,游戏内外的科学家们为了计算三体问题绞尽脑汁,最后也没有得到准确的答案,遗憾的是当系统扩展到三体甚至更多天体时,上述简化不再适用,三体问题因为缺乏通解而成为经典力学的经典难题之一。
【下期预告】星球上无限长摆长单摆的周期
从 的理解入手,从极限的角度理解无限长单摆的周期等相关问题···
的理解入手,从极限的角度理解无限长单摆的周期等相关问题···
对这本《演讲的本质》(my impact)的感受,我想到的了“挂洋头”(Martin Newman),可能也是很多人都说好的商业的东西,对于一个小知识分子来说就如碰到榴莲吧。
“我人生最遗憾的事就是当机会窍门时,我却错过了。”
四陪(这种词其实不太适合书面语,特别是对女“公关”)
被日本誉为“演讲之神”的马丁(对这个说法表示怀疑)(DeepSeek了一下,商界和政界却有这种说法。)
拒绝帮助客人成为乔布斯,培训师要帮助客户呈现更理想的自己。
一、演讲时领导者的必备能力
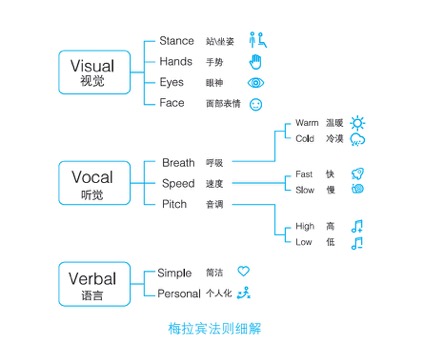
1971年梅拉宾法则:一个人对他人的印象,约7%取决于谈话的语言和内容;音量、音质、语速、节奏等声音要素占38%;眼神、表情、动作等形象因素所占比列高达55%。也就是说,哪怕你听不见对方说话的声音,也能理解对方想要表达的至少一半以上的内容。在视觉visual、听觉vocal、语言verbal的综合作用下,最终形成了别人对你的印象。
不做无意义的动作。拒绝没能量的声音。
人们在最初的两秒的直觉很重要。
最好是把演讲的过程录下来,然后客观地做出分析。
拍好后把声音关掉,专注于自己的形象。
不是演,而是展现更好的自己。
那一刻对方给你百分百的关注和友好。
其实自信不是来自你的内心,而是源于他人。当我们得到他人的肯定时,我们会有信心。
自信是礼尚往来的共赢。你对他人有信心,你乐于肯定对方,对方自然会获得自信,反过来你也会觉得愉快,对方也能从中感受到自信,因为越是自信的人,越能接受和尊重他人。
自信是同一个水平线上的互动,你得引导对方先建立他的自信,才能让对感受到你的自信。而且这还有利于你获取他人的信任,因为当对方觉得你是自信的,自然也更愿意信任你。
“神秘的东方人”,总是千篇一律的样子,面无表情,从不泄露任何信息。
西方人用“绕圈子”来形容中国人说话“抓不住重点”(东方人含蓄吧)
平庸的演员试图让观众相信自己的表演,而杰出的演员则毫无疑问地相信自己的表演。
(很多人)之所以认为自己不擅长演讲,多是因为不重视演讲的价值,认知有偏差。
二、形象是一种科学,不是颜值
手势让话语更有力量。
(男模特很一般啊,青涩;后面那个专职形象的,也就那么回事吧。)(涉及到具体的人,很难和理想的形象关联,卡通或者AI设计或许更好。)
演讲的一个最大原则,也是一个很棒简单的道理:“重要的事情说三遍!”(什么马云孙正义,什么日本申奥,那么几个事来回提及,感觉没那么好。)
盛情款待
像蜜蜂采蜜一样注视观众。(这一点,特别家长会等场合,自己目光游移,要试着改变)
演讲时,我们应该像蜜蜂采蜜一样和观众进行眼神接触···演讲时,将你的眼神专注在几个人身上,对方会感受到你的真诚和尊重,然后你再将眼神慢慢转向其他观众。
如果会话中你能多注意自己的身体状态,你会发现很多事情会随之变化,别人对你的印象也会大有改观。
微笑这一行为会让我们的心情变得更好,微笑不仅仅是心情好的产物。
三、声音是一种人格,不是音色
“如果一个人心中有上帝,那么他的声音应该像溪流的汩汩声或风吹在庄稼的沙沙声那般甜美。”
你主持的节目为什么那么受欢迎?“因为我一分钟说125个字。”
沉默之于演讲,就像父亲之于子女。演讲中,停顿的作用非同小可。
四、内容是一种价值,不是权威
说话太复杂,让人难以听懂。
We must learn to live together as brothers or perish together as fools.
断舍离:断是对于自己不需要的东西,坚决不买;舍是处理掉没用的东西;离是脱离对物质的执着,让自己所处的环境干净、空旷,让自己感觉自在。
“天哪!我自己都懒得听自己的演讲!”
作为交流者,重复是你最好的武器。
五、随时随地提升影响力
(作者以自己很牛的经历,当然是接触了很牛的人的经历,描绘理解的表面)
No Negativity No Status(没有否定,没有等级。)
参差多态,乃是幸福本源。
演讲像是装修房子,先定风格,再论梁柱。(壁纸吧)(建造房子还是装修房子)
危机是表,声誉是本
(“沉默的螺旋”,即大多数人持有的观点成为主流意见,而少数人的观点则逐渐被压制和沉默。)
停顿一定要留有足够的时间,甚至让人以为你忘词了或者出现了失误。
服饰是一种资源,也是一种工具,它可以控制并协助满足个人需求和实现目标。
像国王那样演讲。
如果演讲的目的只是传递信息,为什么不干脆发封电子邮件了事呢?
很多人以为演讲时一项脑力活动,实际上它更多的是身体活动。
我想帮助人们实现的是更好的自己,而不是成为别人。