前一阵子中午跑完步还有时间，就去单杠那找找年少的感觉。偶然发现几位很特别的小朋友，别人在踢足球、打篮球或嬉戏打闹，他们在自行练习和切磋，几日观察下来，除了自律，还有知识储备等···想到最近跑步活动开展的不错，是不是也应该鼓励和赞助几位开展个健身的小社团呢，至于名字想到“逆熵社”之类，鉴于先有了qiutorun[?]，那来个qiutofit何尝不可呢。

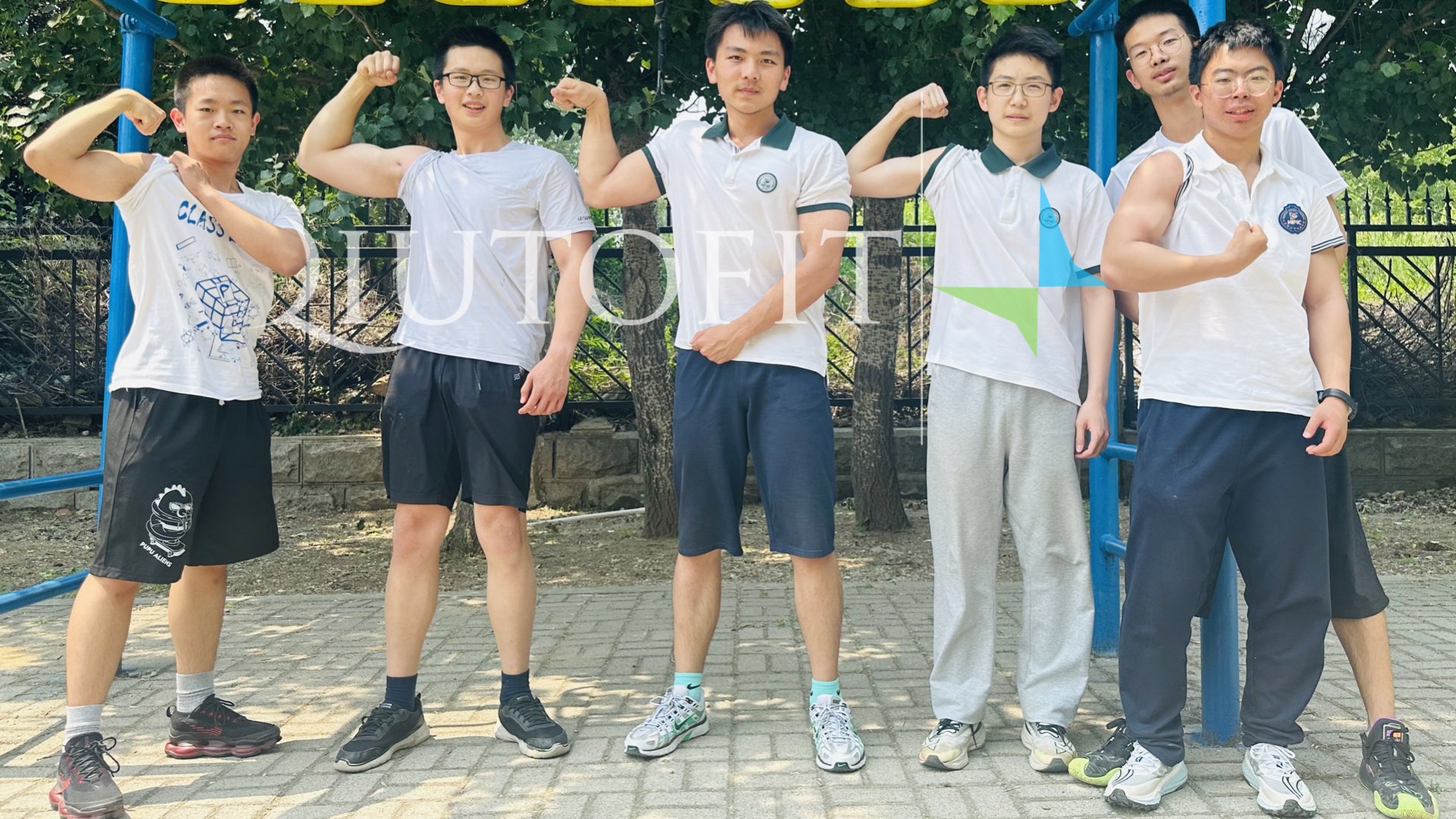
“生命如伙，强健有我。”我喜欢伙伴的“伙”和康健的“健”，因为都有个“亻”的偏旁。等高考结束，月考也结束，相信能有不错的方案。

先预祝高考成功~~~

《反叛的科学家》(The Scientist as Rebel)一代传奇物理大师Freeman Dyson的科学反思
萧秀珊译
一个知识人的诤言
如果把形成共识形容成湖面结冰的话，戴森会不遗余力地在冰面上凿洞。
时间很晚了，然而善恶的选择却在敲着我们的门。
理性的反叛者
二十世纪物理学三大人物，爱因斯坦、霍金和费曼。
狐狸伎俩多，刺猬只懂一种。
科学是人类理性与想象特质的自由发挥。（科学是人类对事物的逐步征服，先是时间与空间，再来是物质那类，然后是自己的身体与其他生物体，最后征服的是自身灵魂中的黑暗与邪恶。）
前言
富兰克林没有受过正规教育，也没有继承大笔财产，但在与欧洲贵族的科学竞赛中，击败了这群博学多闻的贵族们。
富兰克林所展现的反叛是经过深思熟虑的反叛，是由理性与仔细考量所驱动，并非由激情与仇恨所驱使。
（以反叛者的身份去的了伟大的成就，因为他们旨在建立新社会，而不是摧毁旧社会。他也了解传统的价值，他伟大到足以看到事情的两面。）

让胜利者来吧，
当愚昧的堡垒倾倒时，
他们会在墙边找到你的身体！
Mathew Arnold

一、当代科学议题
1、反叛的科学家
他们叫那个倒扣的碗为天空
在那之下被禁锢的我们蠕动着活着与死去
不要举手向它求助
因为它
跟你我一样只会无力打滚
Continue reading »

JQX/进取芯 席明纳第8期（2025.5.14）

在力学问题中，速度关联现象较为常见，而加速度是否也存在类似的关联规律呢？

JQX|Jin
一、绳 / 杆模型
一）例题
如图所示，物块套在固定竖直杆上，通过轻绳跨过定滑轮与小球相连，初始时刻物块与定滑轮等高。已知物块质量 $m_1 = 3\,\text{kg}$，小球质量 $m_2 = 5\,\text{kg}$，杆与滑轮间的水平距离 $d = 2\,\text{m}$，重力加速度 $g = 10\,\text{m/s}^2$，且轻绳和杆长度足够，忽略一切摩擦与空气阻力。现将物块由静止释放，在其下落过程中，求解以下问题：
1. 物块下降的最大距离
设物块下落的最大高度为 $h$，此时小球上升的最大距离为 $h_1$。根据几何关系可知：$h_1 = \sqrt{h^2 + d^2} - d$
机械能守恒定律可得：$m_1 g h = m_2 g h_1$
解得：$h = 3.75\,\text{m}$
2. 系统动能最大时物块的动能
这里有两种方法：
1）写出动能与角度的表达式，进行数学方法求极值。
2）从物理意义上考虑，当系统的重力功率之和为 $0$ 时，系统动能达到最大值。
设物块速度为 $v_1$，小球速度为 $v_2$，根据速度关联关系可知：$v_2 = v_1 \sin\theta$
由重力功率关系可得：$m_2 g v_2 = m_1 g v_1$
对物块和小球组成的系统，运用机械能守恒定律求解动能最大值，可得动能最大值为：$\frac{1000}{53}\,\text{J}$
3. 物块运动的最大速度
1）原答案解析
答案寻找了一个特殊位置：当物块的速度最大时，加速度为 $0$，由于物块和小球被绳牵连，沿绳方向的加速度大小相等，小球的加速度也为 $0$，所以物块和小球同时达到最大速度，分别为 $v_1$ 和 $v_2$。分别对物块和小球列平衡方程得：$F_T \sin\alpha = m_1 g$$F_T = m_2 g \quad \text{(1)}$
由(1)式可求得：$\sin\alpha = \frac{3}{5}$则：$\alpha = 37^\circ \quad \text{(2)}$
如图3所示，由物块和小球沿绳方向的速度大小相等得：$v_2 = v_1 \sin\alpha \quad \text{(3)}$
由系统的机械能守恒：$m_1 g d \tan\alpha - m_2 g \left( \frac{d}{\cos\alpha} - d \right) = \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 \quad \text{(4)}$
联立(2)(3)(4)式解得：$v_1 = \frac{5\sqrt{3}}{3}\,\text{m/s} \approx 2.89\,\text{m/s}$$v_2 = \sqrt{3}\,\text{m/s} \approx 1.73\,\text{m/s}$

2）对原答案的质疑
原答案认为，既然沿绳方向的速度大小时刻相等，沿绳方向的加速度大小一定会相等，并且找到了一个特殊位置，满足两个物体加速度同时为 $0$。但是，这个理论靠得住脚吗？
设物块的速度为 $v_1$，小球的速度为 $v_2$，二者速度关系为：$v_2 = v_1 \sin\theta$
对该速度关系两边求导，可得：$a_2 = a_1 \sin\theta + v_1 \omega \cos\theta$
我们发现，不存在两个物体加速度同时等于0的情况。原答案解析是有错误的。
当物块的速度最大时 $a_{1} = 0$，则有 $a_{2}=\frac{v_{1}^{2}\cos^{3}\theta}{d}$
对物块有 $T\sin\theta = m_{1}g$
对小球有 $T - m_{2}g = m_{2}a_{2}=m_{2}\frac{v_{1}^{2}\cos^{3}\theta}{d}$
对物块与小球组成的机械能守恒，可得 $m_{1}gd\tan\theta - m_{2}g(\frac{d}{\cos\theta}-d)=\frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2}$ 其中 $v_{2} = v_{1}\sin\theta$，
联立解得 $v_{1}\approx3.02m/s$

二）讨论：加速度关联（沿绳方向加速度相等）满足的条件
1. 速度为零
2. 角速度为零
3. $\theta$ 趋近于 $90^\circ$
我们也可以进一步推导公式，发现多出一项即为绳的向心加速度。所以，如果出现旋转，在加速度关联时，就要加上向心加速度这一分量。

三）速度关联的三种推导方法
在绳连接船的系统中，根据沿绳方向加速度相等，可得：$v_2 = v_1 \cos\theta$其中 $\theta$ 为绳与水平方向的夹角。
1. 求导法
设船与岸边距离为 $s$，绳长为 $l$，定滑轮高度为 $h$，根据勾股定理可得：$s^2 + h^2 = l^2$
对时间 $t$ 求导，得到：$2s \frac{ds}{dt} = 2l \frac{dl}{dt}$
其中 $\frac{ds}{dt}$ 表示船的速度 $v_1$，$\frac{dl}{dt}$ 表示人收绳的速度 $v_2$。可得到：$s v_1 = l v_2$
结合几何关系可推导出：$v_2 = v_1 \cos\theta$

2. 微元法
取极短时间 $\Delta t \to 0$，此时绳转过角度 $\Delta\theta \to 0$。过船所在位置 $B$ 作绳初始位置 $OA$ 的垂线 $BE$，由于 $\Delta\theta \to 0$，可近似认为 $|OB| = |OE|$。
人收绳长度：$x_2 = |OA| - |OB| = |AE|$
船运动距离：$x_1 = |AB|$
根据 $v = \frac{\Delta x}{\Delta t}$，有：$|AE| = v_2 \Delta t$ $|AB| = v_1 \Delta t$
又因为 $|AE| = |AB| \cos\theta$，将上述关系代入可得：$v_2 \Delta t = v_1 \Delta t \cos\theta$
约去 $\Delta t$，得到：$v_2 = v_1 \cos\theta$

3. 功率法
考虑到绳为轻质绳，不储存能量，这意味着人拉绳的瞬时功率时刻等于绳对船的作用力的瞬时功率。根据功率公式 $P = F v$，可列出等式：$F v_2 = F v_1 \cos\theta$
等式两边拉力 $F$ 相同，化简后得到：$v_2 = v_1 \cos\theta$
拓展例题：虚功原理
如图所示，一条线密度为 $\lambda$ 的均匀铁链，静止放置于半径为 $R$ 的光滑半圆形台上。铁链两侧对称下垂且恰好落在半圆末端。试求解铁链在最高点处的拉力 $T$。
提示：可以认为铁链向左移动很小一段，相当于拉力做功将末端的一小段质量搬运到了最高点。
$\lambda \cdot \Delta x \cdot g \cdot R = F_T \cdot \Delta x$

二、接触模型
1.在接触模型中，两物体接触处的速度关联通常将接触点处的速度沿接触面切线方向和垂直于接触面方向分解，由于两物体始终保持接触，垂直于接触面方向的分速度大小相等。
而在加速度关联方面，垂直于接触面方向的加速度存在关联关系，具体推导过程与绳杆模型相同。
$v_1 \sin\theta = v_2 \cos\theta$  $a_1 \sin\theta + v_1 \cdot \theta' \cos\theta = a_2 \cos\theta - v_2 \cdot \theta' \sin\theta$
其中：$v_1 \theta' \cos\theta + v_2 \theta' \sin\theta = (v_{1t} + v_{2t}) \cdot \omega = \frac{u^2}{\rho}$  $u$ 为相对速度，$\rho$ 为曲率半径。
若接触面是平面，则垂直于接触面方向的加速度相同。若接触面是曲面，还需考虑向心加速度对加速度关联的影响。这个加速度计算时，速度应为接触点相对于接触面的加速度，半径应为曲率半径。
2. 相对向心加速度的使用
在高中物理中，我们利用向心加速度计算时，带入的速度均为相对于圆心的速度（因为不相对于圆心，也不是圆周运动了）。
例题：两个固定的光滑杆十字放置但不接触，两个质量为 $m$ 的 $A$、$B$ 两球套在杆上并用铰链通过另一长为 $L$ 的直杆相连。初始位置如图所示，轻微扰动 $B$ 球后，求 $A$ 球的最大速度。
方法一：
速度关系：$v_a \cos\theta = v_b \sin\theta$
机械能守恒：$2 g L (1 + \cos\theta) = v_a^2 \left( 1 + \frac{\cos^2\theta}{\sin^2\theta} \right) = \frac{v_a^2}{\sin^2\theta}$
联立解得：$v_a^2 = 2 g L (1 + \cos\theta) \sin^2\theta = 2 g L (1 + \cos\theta)(1 - \cos^2\theta)$
通过求导求极值，可得当 $\theta = \arccos\frac{1}{3} \approx 70.5^\circ$ 时，$v_a$ 取得最大值。
方法二：相对向心加速度（帅）
在实际教学中，计算杆上力的时候，经常使用相对运动的方法列圆周运动。本题可以以B球为参考系，则A球相对B球做圆周运动。
那么在A球受力分析时，要引入惯性力（B球的ma），这个力恰好与A球所受杆的力大小相等方向相反（惯性参考系使用质点系牛二分析水平方向），这两个力合力为零。
所以沿杆方向的力只有杆力和重力分力：$m\frac{v_a^2 + v_b^2}{L} = F_T - mg\cos\theta$
速度最大时，A球竖直方向加速度为0，有$F_T\cos\theta = mg$
再结合机械能守恒和速度关系： $mg(L\cos\theta + L) = \frac{1}{2}mv_a^2 + \frac{1}{2}mv_b^2$、 $v_a\cos\theta = v_b\sin\theta$
解得 $\cos\theta = \frac{1}{3}, \quad v_a = \frac{8\sqrt{3gL}}{9}$，结果与方法一相同。

三、动滑轮模型
一）例题分析
如图，三个已知质量的物块通过轻绳、轻滑轮连接，不计一切阻力，由静止释放，已知重力加速度 $g$，求三者加速度大小各是多少。
设三个物块质量分别为 $m$、$2m$、$3m$，加速度分别为 $a_1$、$a_2$、$a_3$，绳子拉力分别为 $T_1$、$T_2$。
根据牛顿第二定律对三个物块分别列式：
对于质量为 $m$ 的物块：$T_2 - m g = m a_1$
对于质量为 $2m$ 的物块：$T_2 - 2 m g = 2 m a_2$
对于质量为 $3m$ 的物块：$T_1 - 3 m g = 3 m a_3$
同时，根据滑轮的力学关系有：$T_1 = 2 T_2$
根据物块间加速度关联，有：$a_1 - (-a_3) = -[a_2 - (-a_3)]$
联立求解后，可得：$a_1 = \frac{7}{17} g, \quad a_2 = -\frac{5}{17} g, \quad a_3 = -\frac{1}{17} g$
易错点：
1. 左侧滑轮的加速度关联（换参考系）问题。
2. 滑轮的力学关系。
二）绳拉船问题加滑轮
如果将绳拉船问题的船加上一个滑轮，另一端水平连接到岸边，如黑板左中图所示。那么，这个情况下的速度关联如何？
方法一：求导法
$v_2 = \dot{x}$   $v_1 = \dot{L}$
$L = l + x = \sqrt{x^2 + h^2} + x$
对时间求导，$v_2 = \frac{v_1}{\cos\theta + 1}$
方法二：功率法
$F v_1 = F v_2 + F \cos\theta \cdot v_2$
方法三：微元法
$v_1 \cdot \Delta t = v_2 \Delta t (1 + \cos\theta)$
从物理意义上来看，滑轮的引入在原有速度关联的基础上，增加了水平绳子缩短的速度。

【下期预告】邀请高一六班刘而行同学交流“非惯性参考系与惯性力”···

又多了一位我要穷追的作家，就如我最初看到弗里曼·戴森的书一样。难怪霍金称赞他是最会讲故事的物理学家呢（Leonard Mlodinow never fails to make science both accessible and entertaining），书中真读到史蒂芬·茨威格的影子。很庆幸我有两本，目前我读的科学史相关的书中，能与之比较的估计也就卡约里的《物理学简史》[?]。比如看看博士的宗谱，赵教授与蒙洛迪诺的物理阅历比较起来还是两个级别吧，但最大的区别还是对于科学史的细节把握和连贯性处理等方面。考虑到赵教授所处的环境，他的书[?]已经是很难得也很珍贵了。有机会正好再看看弗里曼·戴森的《反叛的科学家》的台版。
台版翻译为《科学大历史》比较准确吧，日本翻译的似乎是《人类科学的400万年史》，相比龚睿翻译的《思维简史》，最初还以为是心理学著作呢，都忘记了什么原因购买的，还买重了哈哈哈，封面设计就不吐槽了，毕竟中信进入了好书，翻译的读起来也很顺畅，除了个别小错误，比如赫兹并没能活到76···
Leonard Miodinow并没有走入两朵乌云的俗套，这很有胆识，更是自信。
献给西蒙·蒙洛迪诺
Continue reading »

JQX/进取芯 席明纳第7期（2025.5.8）

无限常摆长单摆周期问题

零、关于$T = 2\pi\sqrt{\frac{R}{g}}$
这个公式是Qiusir在JQX第四期与新疆部学生进行头脑风暴时用到的公式。
根据天体运动中万有引力充当向心力，可以推导近地卫星（贴地卫星）的周期公式，为$T = 2\pi\sqrt{\frac{R}{g}}$，这个公式很容易让人想到摆长为R单摆的周期，可事实上是这样吗？

一、关于$T = 2\pi\sqrt{\frac{r}{g}}$
后来讨论的过程中，学生提到他想表达的公式是这个。这个公式可以看做一个小球在圆轨道做小振幅往复运动的周期（等效单摆）。

二、从能量角度推导简谐振动的动力学方程和单摆周期公式
1. 简谐运动
简谐运动满足能量守恒方程：$\frac{1}{2}mv^{2}+\frac{1}{2}kx^{2}=E$，
简化这个方程，即当动力学方程满足$\frac{k}{m}x^{2}+\dot{x}^{2}=C$（$C$为常数）时，可判定为简谐运动。其中，$\frac{k}{m}$定义为角频率$\omega$的平方。
2. 单摆
选取单摆摆动的最低点作为重力势能零点。对于摆角为$\theta$的任意位置，根据机械能守恒定律，单摆系统的总能量$E$满足方程$\frac{1}{2}mv^{2}+mg(l - l\cos\theta)=E$，其中$m$为摆球质量，$v$为摆球线速度，$l$为摆长，$g$为重力加速度。
根据圆周运动线速度与角速度关系$v = \omega l$，且角速度$\omega$可表示为摆角$\theta$对时间的一阶导数$\omega=\dot{\theta}$，同时，利用小角度近似条件（当$\theta\approx0$时），$\cos\theta$可展开为$\cos\theta\approx1-\frac{\theta^{2}}{2}$。
将上述关系代入能量方程，可得：$\frac{1}{2}m\cdot\dot{\theta}^{2}\cdot l^{2}+mg\cdot l\cdot\frac{\theta^{2}}{2}=E$

由于在小角度下$\theta\approx\frac{x}{l}$（$x$为摆球偏离平衡位置的水平位移），将其代入上式，整理后得到：$\dot{x}^{2}+\frac{g}{l}x^{2}=C$。对比简谐运动的动力学方程，可得出单摆运动的角频率$\omega^{2}=\frac{g}{l}$。

可得到单摆的周期公式：$T = 2\pi\sqrt{\frac{l}{g}}$

三、无限摆长问题的提出
我们知道单摆的周期公式是$T = 2\pi\sqrt{\frac{l}{g}}$，现在我们来思考一下，当摆长$l$趋于无穷大，还有当摆长$l$等于地球半径的时候，这个周期会是多少呢？
我们先来推导一下单摆周期公式。
当单摆的摆角$\theta$极小时，重力沿圆弧切线方向的分力$F = mg\sin\theta$作为回复力。

由于摆角$\theta$极小，此时$\sin\theta\approx\theta$，且$\theta=\frac{\overset{\frown}{OP}}{l}\approx\frac{x}{l}$，有回复力$F = - \frac{mg}{l}x$。设$k = \frac{mg}{l}$，则回复力$F=-kx$，这意味着单摆在摆角很小时做简谐运动。把$k$代入简谐运动周期公式$T = 2\pi\sqrt{\frac{m}{k}}$，便能推导得出相应结果。
那么，当摆长无限大时，周期应该为多少呢？是无穷大吗？我们慢慢道来，先来看一下这个情况：

四、近地卫星周期
万有引力充当向心力，可以推得$T = 2\pi\sqrt{\frac{R}{g}}$，另外，如果使用近地卫星周期可以求密度的结论：$\rho = \frac{3\pi}{GT^{2}}$，将密度反向带回，也可以推导周期。

五、"地下铁"周期
我们假设在地球赤道对称两级挖通一个隧道，设地球半径为$R$，质量为$M$。在隧道一端由静止释放一个物体，质量为$m$，与地心的距离记为$x$。我们来分析一下这个物体的运动。

我们知道理想球壳对内部物体的引力合力为零，在这个物体在隧道里面运动中距离地心$x$处时，所受引力等效于半径为$x$的部分地球对其施加的引力。
球体质量公式$M = \rho\times\frac{4}{3}\pi R^{3}$（$\rho$为地球平均密度），可推导出半径为$x$的球体质量$M_{x}=\rho\times\frac{4}{3}\pi x^{3}$。结合$F = G\frac{Mm}{r^2}$、$mg = G\frac{Mm}{R^{2}}$、$M = \rho\times\frac{4}{3}\pi R^{3}$，可得到$F = -\frac{mg}{R}x$，图像请见黑板。带入简谐周期公式，容易算得$T = 2\pi\sqrt{\frac{R}{g}}$。
可以发现，"地下铁"周期的计算结果，与近地卫星的周期数值是相等的，如果在地下铁释放物体的同时，在地面同时发射一颗近地卫星，会发现二者在各自轨道上的运动具有同步性（投影共线），这一现象背后其实蕴含着简谐运动是匀速圆周运动分运动的物理规律。

如果我们将地下铁的轨道换到更高纬度，经过计算（涉及到受力分解等，过程请尝试自行推导）依然可以算得$T = 2\pi\sqrt{\frac{R}{g}}$，如果我们进一步提高纬度，将纬度极限到北极附近非常小的一部分，那么这个往复运动，应该可以视为无限摆长的单摆运动（摆长无限，近似于直线运动），那么，这个无限摆长的单摆周期，竟然不是无穷大，而是$T = 2\pi\sqrt{\frac{R}{g}}$。

六、单摆周期公式的修正
通过前面的讨论我们发现，传统单摆周期公式在特殊情况下需要修正。在推导单摆公式时，我们默认重力场类似匀强电场一样方向不变，但实际将视角扩大到地球半径尺度下，我们可以发现其实重力方向是指向地心（忽略自转），那么修正后的单摆周期公式是什么呢？
如黑板七图所示，设摆长为$l$，地球半径为$R$。万有引力即为重力，$G \frac{Mm}{R^2}=mg$
回复力$F = mg \sin(\beta + \alpha)$
基于小角度近似关系$\sin\theta \approx \theta$，有$\sin(\beta + \alpha) \approx \beta + \alpha$
再根据小角度几何关系，有$\beta = \frac{x}{R}, \quad \alpha = \frac{x}{l}$
考虑到回复力方向与位移方向的反向关系，进而得到：$F = -mg \left( \frac{1}{R} + \frac{1}{l} \right) x$
回复力系数为$k = mg \left( \frac{1}{R} + \frac{1}{l} \right)$，代入简谐振动周期公式 $T = 2\pi\sqrt{\frac{m}{k}}$，
综上，单摆周期的最终表达式为：$T = 2\pi\sqrt{\frac{Rl}{g(R + l)}}$
这个公式中的摆长，可以等效为两个摆长并联的结果，我们前几期探讨了约化质量也是这个模式，这个难道是"约化长度"？

七、单摆公式修正后的结论
根据修正公式，我们可以发现以下结论：
当l相对R足够小时，该公式就近似于传统单摆周期公式，这也解释了为什么在日常使用传统公式计算普通单摆周期时能得到较为准确的结果。
而当l与R处于相近数量级时，二者差异显著，必须使用修正公式进行计算，
当$l = R$时，$T = 2\pi\sqrt{\frac{R}{2g}}$。
当 $l$无限大时，单摆的周期 $T = 2\pi\sqrt{\frac{R}{g}}$。该结果与此前推导的近地卫星周期、"地下铁" 周期数值吻合。

八、静电场中的简谐运动
我们再来说说关于电场的问题。如黑板8图，假设有一个正电荷$4q$和一个负电荷$q$，固定在距离为$l$的位置上，延长线有点$O$，与负电荷q 的距离也是$l$。
我们来分析一下在$O$点两侧极短的距离内，有一个正电荷$q_{0}$释放之后的运动情况：
根据库仑定律可得电荷所受合力$F = \frac{4k q q_0}{(2l + x)^2} - \frac{k q q_0}{(l + x)^2}$（其中$q_{0}$是释放的电荷）
我们使用AI软件帮我们进行一些体力操作，把这个力$F$泰勒展开展开一下，$F = \frac{k q q_0}{l^3}x - \frac{9k q q_0}{4l^4}x^2 + \frac{7k q q_0}{2l^5}x^3 + \cdots$
因为$x$远远小于$l$，所以我们可以把一些高阶无穷小项忽略掉，有$F = - \frac{q_{0}}{l^{3}}x$，满足简谐运动回复力关系。
从势能的角度来看，我们知道势能和功的关系是$W = - \Delta E_{p}$，我们对势能求导就可以得到力。同样的，我们如果写出势能与位移的表达式，进行求导，同样也可以得到力的表达式。

九、势能的极值附近，物理做简谐运动
肖老师补充：其实对于势能极值的位置，在附近做往复运动大多（并不是所有）可以认为是一种简谐运动。
如果将势能的表达式进行求导，泰勒展开后忽略高阶小量，可以得到力与位移的关系（满足回复力形式），再将力进行求导，得到的数值即为回复力常量k，进而可以求解周期等。
其实，我们在第二部分用能量进行求解单摆周期的过程，完全可以只分析势能，推导过程可以非常简化如下：
单摆的重力势能表达式为：$E_{p}=mgl(1 - \cos\theta)$
当摆角$\theta$很小时（满足$\cos\theta \approx 1 - \frac{\theta^{2}}{2}$），重力势能可近似为：$E_{p}=mgl\cdot\frac{\theta^{2}}{2}$
结合单摆小角度摆动时，摆球位移$x$与摆长$l$、摆角$\theta$的关系$\theta \approx \frac{x}{l}$，进一步推导可得：$E_{p}=\frac{mg}{2l}\cdot x^{2}$
求二阶导数，得到$E_{p}''(x)=\frac{mg}{l}$，即为k值。

十、利用泰勒展开进一步分析
势能的一阶导为该势能所对应的保守力：$F(x) = -\frac{dU}{dx}$，在平衡位置附近，力关于位置近似呈线性关系：$F(x) \approx -k(x - x_0)$，这与简谐振动的回复力形式相同。因此物体近似做简谐振动。其中$k = \left. \frac{d^2U}{dx^2} \right|_{x_0}$，是等效劲度系数。
泰勒展开的一般形式为：$f(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \frac{f^{(3)}(a)}{3!}(x - a)^3 + \cdots + \frac{f^{(n)}(a)}{n!}(x - a)^n + \cdots$
我们把势能U(x)在平衡位置附近展开得到：$U(x) = U(x_0) + (x - x_0) \left. \frac{dU}{dx} \right|_{x_0} + \frac{1}{2}(x - x_0)^2 \left. \frac{d^2U}{dx^2} \right|_{x_0} + \cdots$，由于势能在平衡位置的一阶导数为零，对于足够小的位移，略去三阶以后的项，可近似得到：$U(x) \approx U(x_0) + \frac{1}{2}(x - x_0)^2 \left. \frac{d^2U}{dx^2} \right|_{x_0}$。
简谐振子势能的标准形式为：$U(x) = \text{C} + \frac{1}{2}k(x - x_0)^2$，因此我们可以看出等效劲度系数k为：$k = \left. \frac{d^2U}{dx^2} \right|_{x_0}$。

JQX|Jin
本期研讨Qiusir由单摆入手，通过揭示传统模型在无限摆长条件下的矛盾，修正了考虑重力方向变化的单摆周期公式，并验证了在常规单摆、无限摆长下的自洽性。更帅的是，进一步通过势能泰勒展开法，阐明简谐运动的普适性——平衡位置附近的势能二阶展开决定回复力系数，统一解释了单摆、电场振动等周期性现象。
这一过程逻辑严谨又前后呼应，不仅优化了单摆模型，更凸显物理中通过打破理想假设、探寻真实系统的研究：从矛盾出发，以数学重构模型，最终实现规律的本质性统一。

【下期预告】加速度的关联···
速度关联问题是高中物理运动合成中的难点之一。速度可以关联，加速度也可以关联吗？
下次席明纳，金老师将从一道经典习题入手，探寻三种常见模型的速度、加速度关联的本质，敬请期待。