三 08

力的作用点的位移

教学|〖基础物理〗 qiusir 2012

通过动滑轮拉动物块，力F始终与水平成角theta，则此过程中力F做功多少？

常见错误1、W=FS；常见错误2、W=FScos\theta；常见答案3、W=FS+FScos\theta
通过功定义直接求解的答案4、W=F2Scos\frac{1}{2}\theta\times cos\frac{1}{2}\theta（力的作用点在绳端）虽结果通3，但3正确的结果里却有关键的盲点。
当然也可等效成水平力和成theta角的两个F共同作用，此时力的作用点在物体上，位移是水平S，合力是如果是F_{net}=2Fcos\frac{1}{2}\theta\times cos\frac{1}{2}\theta。

workl

更简便的办法是把绳端位移看成两个向量合成...
W=\vec F\cdot\vec S=\vec F\cdot(\vec S_{1}+\vec S_{2})=\vec F\cdot\vec S_{1}+\vec F\cdot\vec S_{2}
W=FS+FScos\theta
错误的结果不乏正确的成分，而正确的结果往往有忽视细节的运气。如此对课堂上正误评判边界需模糊，而自我修正也是探究的意义。

W = \int \frac{d\vec{p}}{dt} \cdot d\vec{s} = \int m \frac{d\vec{v}}{dt} \cdot d\vec{s} = \int m \vec{v} \cdot d\vec{v} =\frac{1}{2} \int m d (\vec{v} \cdot \vec{v}) = \frac{1}{2}mv^2 + C_0
E_r = \frac{1}{2} \int v^2 dm = \frac{1}{2} \int r^2 \omega^2 dm = \frac{1}{2} \omega^2 \int r^2 dm = \frac{1}{2} I \omega^2
P.S.常用数学符号的 LaTeX 表示方法

On this day..

One Response to “力的作用点的位移”

  1. qiusir Says:
    2月 4th, 2018 at 21:10

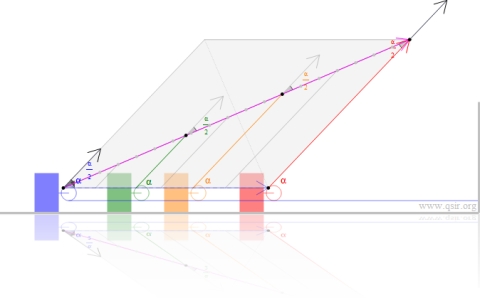
    崔学禹同学从恒力做功（类别重力功）的角度考虑，迎刃而解……