我们要变更好/单摆

“世界会不会变好不重要，我们要变好才重要。”网上没查到是不是诺贝尔说的，不过这话对莫名焦虑的人来说也不是没有一点道理:)
上课带领学生推双星的公式，$$\frac{L^3}{T^2}=\frac{G(m_1+m_2)}{4\pi^2}$$，类比开普勒第三定律很容易记忆…而对地球贴地卫星周期公式化简，$$\frac{R^3}{T_1^2}=\frac{GM}{4\pi^2}$$，$$T_1=2\pi \sqrt{\frac{R^3}{GM}}$$，$$T_1=2\pi \sqrt{\frac{R}{g}}$$
类比单摆的公式，$$T=2\pi \sqrt{\frac{l}{g}}$$，以及圆锥摆的周期公式$$T=2\pi \sqrt{\frac{lcos\theta}{g}}$$，很容易建立起关联。巧妙的是$$T=2\pi \sqrt{\frac{R}{g}}$$也是地球上摆长无限的单摆周期，这个时间还是穿越地心隧道（简谐振动）时间的二倍。

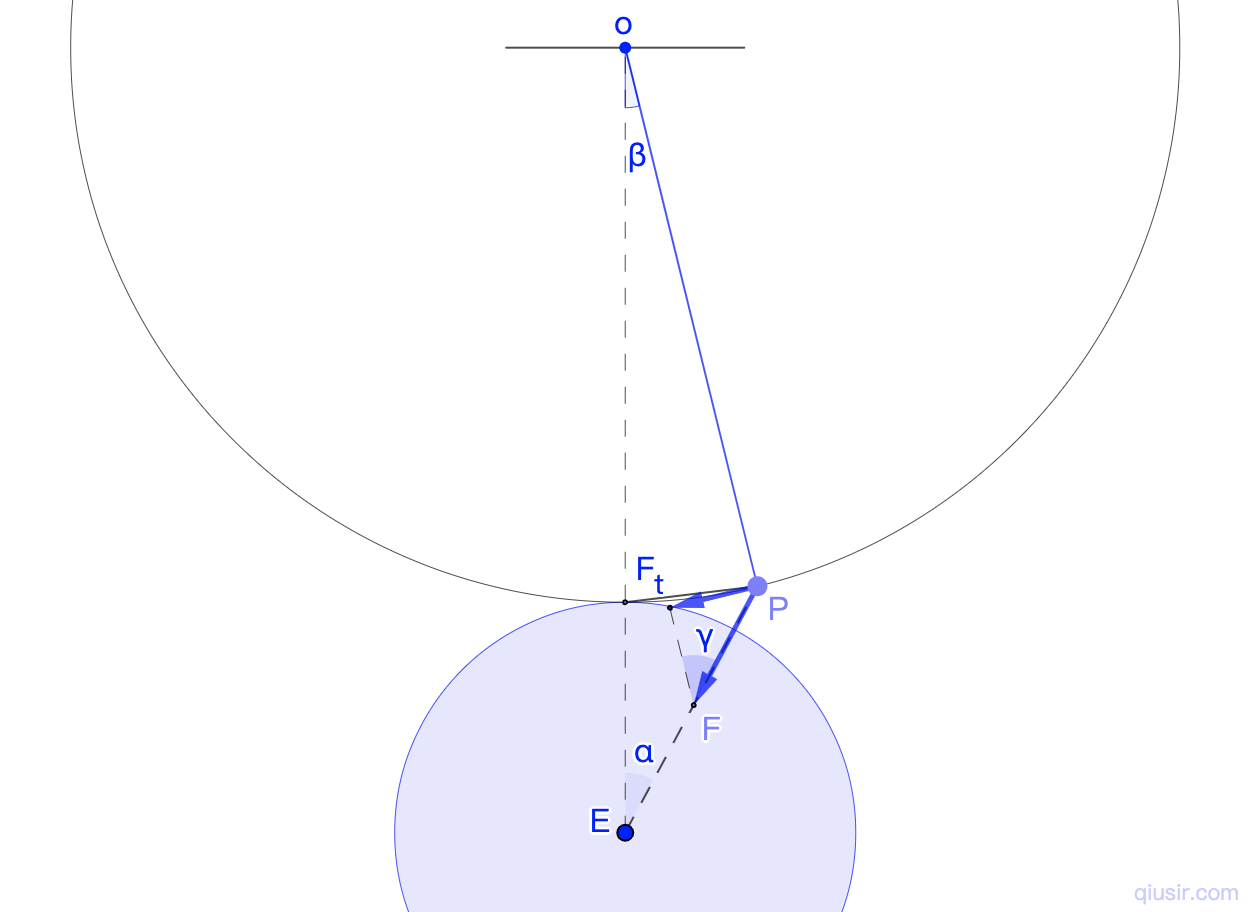
和简谐振动一章推到单摆的周期很接近，设想地面上（可以设想是在很高建筑上）悬点o悬挂摆长l的单摆（摆角很小，一样能近似简振的），万有引力的切向分力提供回复力。
摆球在地表，所有有$$\frac{GMm}{R^2}=mg$$，$$F_t=mgsin(\alpha+\beta)$$，利用小角度$$sin\theta\approx\theta$$，$$F_t=mg(\alpha+\beta)$$，因为小角度，位移大小近似弧长也近似水平…$$F_t=-mg(\frac{1}{R}+\frac{1}{l})x$$
套用弹簧振子周期公式，$$T=2\pi\sqrt{\frac{m}{k}}$$，得$$T=2\pi\sqrt{\frac{Rl}{g(R+l)}}$$
带入特殊值到上述公式，比如摆长远小于地球半径，$$T=2\pi \sqrt{\frac{l}{g}}$$(l=1m,T约2s)；比如摆长为地球半径，$$T=2\pi \sqrt{\frac{R}{2g}}$$（1h）；比如摆长远大于地球半径，$$T=2\pi \sqrt{\frac{R}{g}}$$(1.4h)…

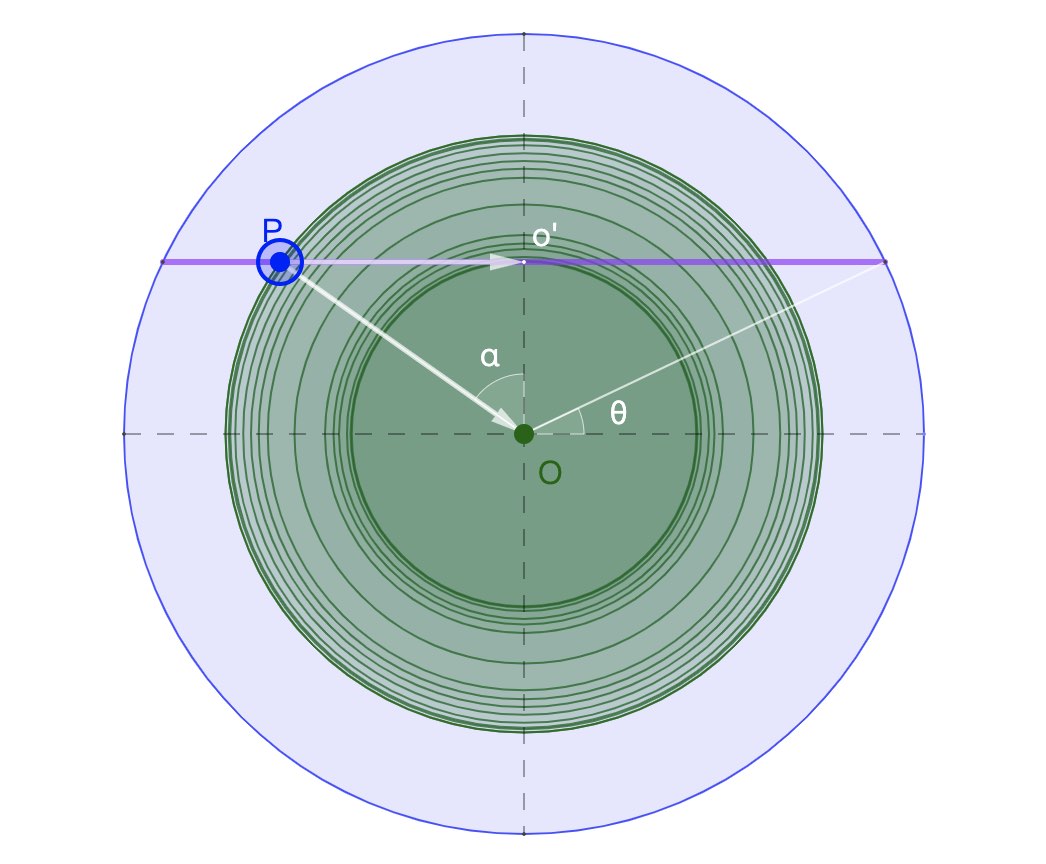
关于贯穿地球的地下铁通行时间的推算，也是用简谐振动的周期。由于球壳对球壳内物体的万有引力为零，所以物体穿行地球时所受的万有引力仅与此处内部球体有关，$$F=\frac{GMm}{r^2}=\frac{Gm\rho\frac{4}{3}\pi r^3}{r^2}$$，$$F_x=-Gm\rho\frac{4}{3}\pi rsin\alpha=-kx$$…
继续套用弹簧振子周期公式，$$T=2\pi\sqrt{\frac{m}{k}}$$，且$$gR^2=GM=G\rho\frac{4}{3}\pi R^3$$，化简后，$$G\rho\frac{4}{3}\pi=\frac{g}{R}$$，得$$T=2\pi \sqrt{\frac{R}{g}}$$，且与$$\theta$$无关。
如果是横贯地心的地下铁，不仅时间和贴地卫星周期相同，更是大撒心心相映的狗粮（圆周运动的投影点）…
当然，这个周期也是和地球半径（大小）无关的，由Kepler’s Law III，$$T=\sqrt{\frac{3\pi}{G\rho}}$$。地球的平均密度大概是水的5.5倍，对于更高密度的星体，这个运行周期要小得多，如果是中子星内部的隧道…
X上看到这种推导…


物理作为高考理科的主力是要背很多的锅，不单是计算不准的数学锅，还有审题失误的语文锅，以及基础知识相关的地理锅、化学锅等等，甚至偶有符号乱用的英语锅… ​

数学L老师就曾提出过[?]上面梗图的困惑。地球自转的线速度$$v_0=\frac{2\pi R}{T_0}$$=0.464km/s，1670km/h…