
王冠棋 NEYC 2024 10
早就发现10班王冠棋同学自行整理的笔记质量很高,偶尔还主动来分享。当时就想,要是这孩子能坚持下去,会像贾钟哲学长的笔记那样[?],毕业后扫描成册会成为后来者的福利呢。
放假前他主动来借“求师得高考物理101”的小册子,说假期高三复习用,当时我还有点怀疑这热情的时效。开学后,不仅那本小册子完成(一些被他看上的题目直接剪掉贴到他的本子上了,这种事我是能忍的)。上周他更是主动来分享了他自己编制的小题目,不仅题目让我眼前一亮,这种从更高视角来复习的方式让我觉得很好。
不单是鼓励,更是督促,特地建了这个页面,用来记录他高三复习的点滴,我们都加油。
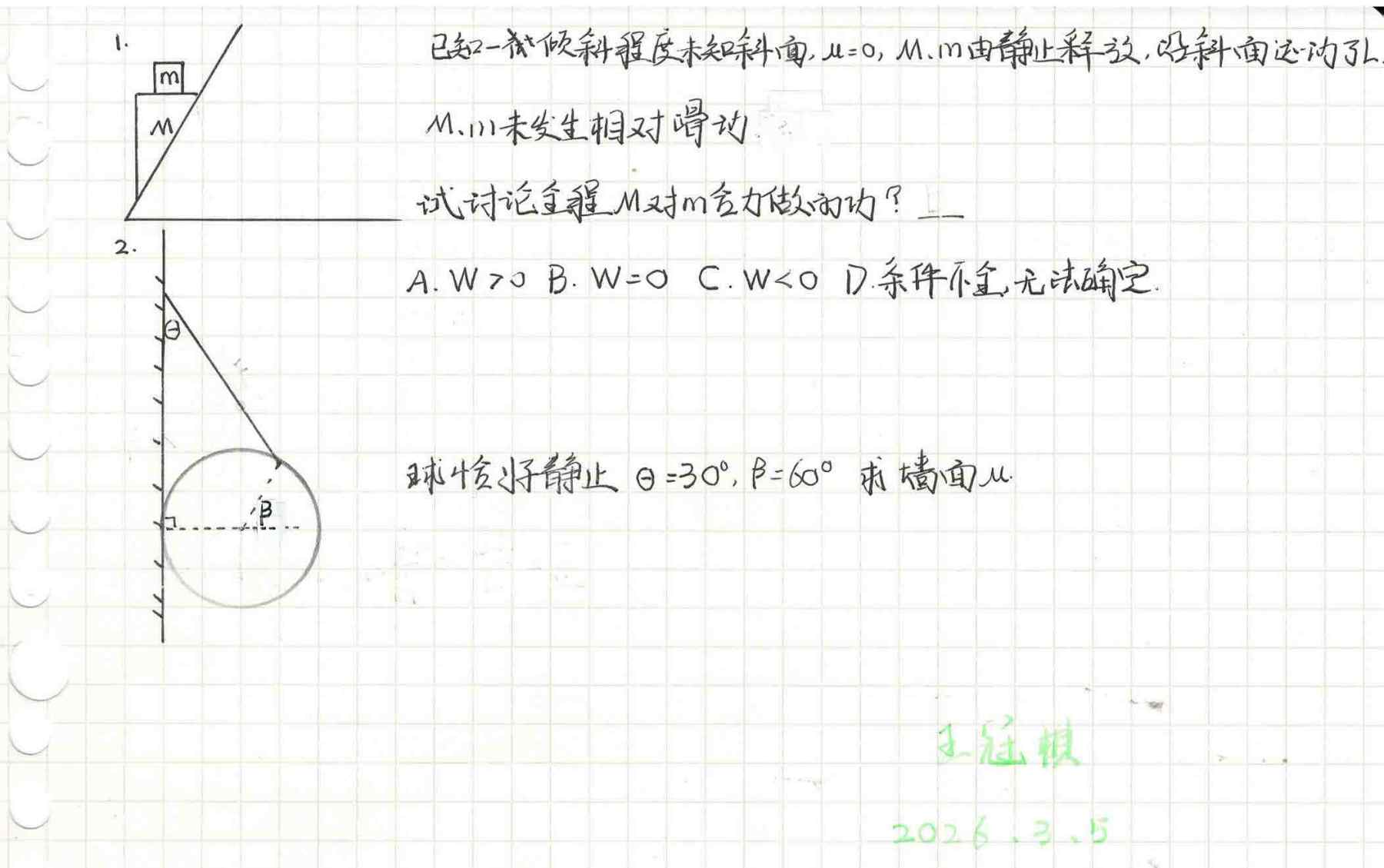
先来两个力学自创小题目,答案在评论区。

