05.曲线运动

平面的匀速圆周运动$$r(t)=\begin{pmatrix} rcos(\omega t)\\ rsin(\omega t)\\0\end{pmatrix}$$，$$v(t)=\begin{pmatrix} -r\omega sin(\omega t)\\ r\omega cos(\omega t)\\0\end{pmatrix}$$
$$a(t)=\frac{d}{dt}\begin{pmatrix} -r\omega sin(\omega t)\\ r\omega cos(\omega t)\\0\end{pmatrix}=\begin{pmatrix} -r\omega^2 cos(\omega t)\\ -r\omega^2 sin(\omega t)\\0\end{pmatrix}=-r\omega^2 r(t)$$
0、相对运动 $$v_{ab}+v_{bc}=v_{ac}$$
1、曲线运动
曲线运动一定是变速运动；曲线运动的物体一定受力；曲线运动可以是匀变速运动。
$$\mathbf{a} =\mathbf{a}_{tan}+\mathbf{a}_{norm}=\frac{d(v\mathbf{e}_{tan} )}{dt}=\frac{dv}{dt}\mathbf{e}_{tan}+v\frac{d\mathbf{e}_{tan}}{dt}$$
2、运动的合成与分解
交点的速度；同一根绳子／竿上的速度／角速度
渡船问题，如果船的速度小于河水的速度，如此情况下的航行的最小航程。
而沿某一方向可能有两个解。
3、探究平抛运动的规律
抛体projectile，拉丁文pro-向前，ject扔出去
（关于平等，地球对万物的力因为质量不同而不同，但都是具有相同的g，而特别的地区g也不同，这是一种平等的理解）
对匀变速运动物体相同时间间隔内位移增量等于aT^2要更熟练解决，还要对数字有更好的理解。
4、抛体运动的规律
位移和水平的夹角；速度和水平的夹角；相当于从中点发出的。
射程的问题；最高点竖直速度为零。

匀变速曲线运动平均速度$$\frac{x}{t}$$、$$\Delta x=aT^2$$的向量性以及和中间时刻瞬时速度等可以从匀变速直线运动迁移过来。
(eg:t=1\3\5经过(0,0)(8,0)(8,6)加速度2.5)

斜抛运动坐标系变换看运动合成。（斜的匀速直线运动和自由落体的叠加）
$$L=v_0t$$
$$x=v_0cos\alpha t=L cos\alpha$$
$$y=v_0sin\alpha t-\frac{1}{2}gt^2=L sin\alpha-\frac{1}{2}gt^2$$
5、圆周运动
$$\frac{\Delta r}{r}=\frac{\Delta v}{v}$$
两边同除以$$\Delta t$$
$$\frac{\Delta r}{r\Delta t}=\frac{\Delta v}{v\Delta t}$$，$$\frac{v}{r}=\frac{a}{v}$$
6、向心加速度
通过速度的水平和竖直分量的导数，求解出水平和竖直的加速度，求解合加速度。
7、向心力
8、生活中的圆周运动
公路在通过水库泄洪闸下游时常常要修建凹形桥，也叫过水路面。

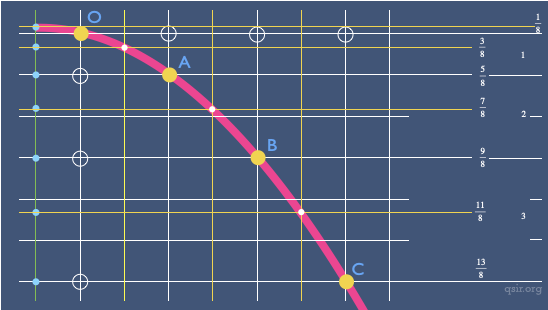
勾股定理求位移大小后通过平均速度求$$v_A$$
·一道运动学题目的多种解法[?]
·等速圆周的向心力证明[?]